Абораторная работа №3 Построение матрицы жесткости для системы упругих элементов.

Элементы теории.

Пусть имеется упругий линейный элемент, например, пружина жесткостью k, (Н/м). Элемент ограничен двумя узлами i и j, где к нему приложены силы f_i и f_j ,(Н), которые вызывают смещения узлов u_i и u_j, (м), вызывая деформацию, например, удлинение элемента, равную разности перемещений его концов: .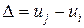

Силу, направленную с положительным направлением координатной оси (например, Ох), принято считать положительной. Силу, сонаправленную с отрицательным направлением координатной оси – отрицательной.

По определению, коэффициент жесткости k численно равен силе, вызывающей деформацию элемента на единицу длины, поэтому зависимость между силами f_i и f_j и вызываемыми ими деформациями равны:

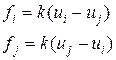(1)

Равенства (1) можно записать в матричной форме:

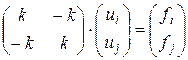(2)

Или в более лаконичной форме

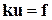(3)

Здесь k симметричная матрица, называется матрицей жесткости упругого элемента, u–вектор –столбец перемещений, f –вектор приложенных сил.

Рассмотрим систему из двух последовательно соединенных упругих элементов (двух пружин жесткостью k₁ и k₂).

В этой системе помимо внешних сил действуют еще и внутренние силы, приложенные к общей точке соединения элементов (общем узле).

В i –ом узле m-го элемента могут действовать несколько сил, которые мы будем обозначать через 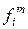, результирующие этих сил обозначим через .

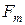В рассматриваемом случае i=1,2,3, а m=1,2, на узел 1 действует сила 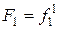, на узел 2 сила 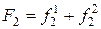, на узе 3 сила: .

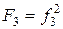В соответствии с равенством (2) для элементов системы можно записать:

Для первого элемента:

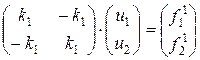
Для второго элемента:

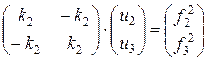
Для составления матрицы жесткости системы из двух последовательно соединенных упругих линейных элементов рассмотрим равновесие сил, действующих на каждый из узлов, перемещения которых обозначим как Δ_i:

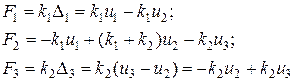
Перепишем эти равенства в виде линейной системы:

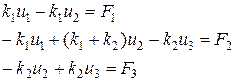(4)

Линейную систему (4) можно записать в матричной форме:

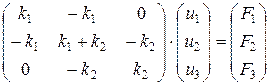(5)

или, в прежнем в виде матричного уравнения (2):

.

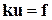Здесь k матрица жесткости системы является первым сомножителем равенства (5).

Для наглядного представления о способе получения матрицы жесткости данной системы элементов, мысленно выделим матрицы жесткости упругих элементов 1 и 2 в отдельности. В виде подматриц они расположены на главной диагонали матрицы k и «сцеплены» в общем узле 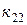.Их главные диагонали совпадают с главной диагональю общей матрицы жесткости и на ней же стоят суммы жесткостей элементов системы, примыкающих друг к другу.

Пример 1.

Описать растяжение двух последовательно соединенных пружин с жесткостью 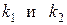жестко закрепленных на одном конце (узел 1).Найти перемещения второго и третьего узлов и реакцию опоры в первом узле.

Решение

Предположим, что узел 1 системы жестко закреплен и перемещаться не может (u₁=0), в этом узле в нем силой F₁ будет реакция связи с опорой, а в узлах 2 и 3 приложены равные силы F₂=F₃=Р.

При этом равенство (5) запишется в виде:

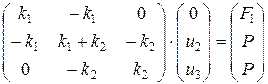
Выполняем умножение матриц.

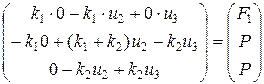
Приравнивая сходственные элементы столбцов, получим систему из трех уравнений с тремя неизвестными :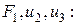

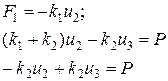
Решая эту систему, получим:

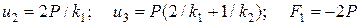
ример 2.

Систему образуют три последовательно соединенные пружины с жесткостью k₁=100Н/см, k₂=200 Н/см и k₃=100 Н/см соответственно. Концы системы закреплены (узлы 1 и 4) u₁ = u₄ = 0. В узле 3 между второй и третьей пружинами приложена продольная сила Р=500Н, сжимающая третью пружину, на узел 2 внешние силы не действуют .

Определить: 1) глобальную матрицу жесткости системы; 2) смещения узлов 2 и 3; 3)реакции связи в первом и четвертом узлах; 4) усилие в элементе 2.

Решение

Запишем матрицы жесткости для каждого из элементов системы:

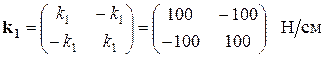
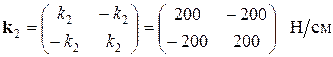
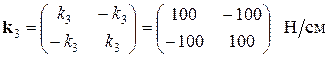
Глобальная матрица жесткости строится исходя из принципа суперпозиции, и имеет вид симметричной и ленточной матрицы:

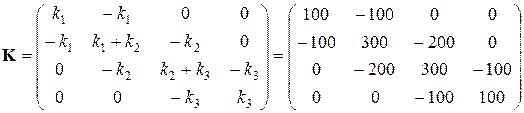
Уравнение равновесия для всей системы упругих элементов имеет вид:

(*)

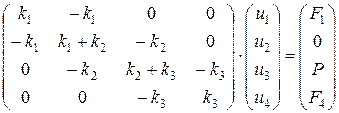Чтобы учесть в данном уравнении граничные условия u₁ =0 и u₄ = 0 надо вычеркнуть в матрице К первую и четвертую строки, первый и четвертый столбцы. При этом получаем:

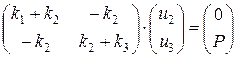
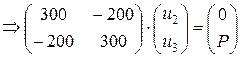
При умножении матриц получаем систему:

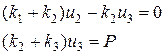
откуда

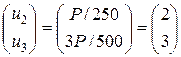
Итого, имеем следующие значения смещений: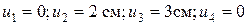

Система (*) принимает вид:

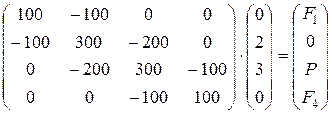
Умножая первую и четвертую строки матрицы жесткости на вектор-столбец смещений и приравнивая первому и четвертому элементам столбца в правой части, получаем:

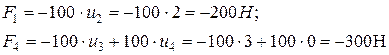
Конечно-элементным уравнением для элемента 2 системы будет

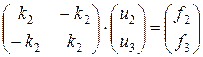
Подставляя численные значения, получим

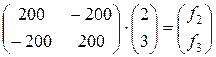
Откуда

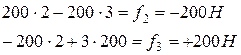
Итого .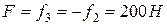

Задача решена полностью.

ример 3.

Двухступенчатый стержень с двумя ступенями одинаковой длины l, имеющих площади поперечного сечения ступеней S₁ и S₂ заделан с левого торца в стену и нагружен на правом торце усилием Р, направленным вдоль оси стержня. Модуль упругости материала стержня – Е. Составить матрицу жесткости стержня, определить перемещения сечений 1, 2 и 3.

Решение

Разобьем стержень на два участка (элемента) 1 и 2 и введем на их концах узлы 1, 2 и 3 где будем определять неизвестные перемещения u₁,u₂ и u₃.

Рассмотрим отдельно один элемент длиной l и площадью поперечного сечения S к концам которого приложены силы Р1 и Р2, направленные вдоль оси стержня. Под их действием торцы стержня (узлы) имеют осевые перемещения l₁ и l₂. Связь между усилиями и перемещениями даются соотношениями:

;

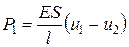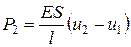
Систему из этих двух равенств можно записать в матричной форме

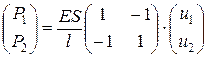(п.3.1)

или

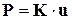(п.3.2)

Здесь матрица жесткости элемента, связывающая узловые усилия и перемещения имеет вид:

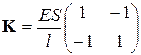(п.3.3)

Составим уравнение равновесия для всего двухступенчатого стержня, объединяя полученные соотношения для элементов 1 и 2, записанные с учетом равенства (п.3.3). Так как стержень состоит из нескольких элементов, то его глобальная матрица жесткости должна включать матрицы жесткости этих элементов. Это включение состоит в том, что их главные диагонали должны совпадать с главной диагональю глобальной матрицы жесткости и состыковываться в узле 2.

На основании (п.3.1) общую систему уравнений равновесия можно записать в виде матричного равенства:

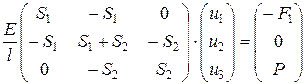(п.3.4)

Здесь 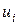- перемещение i – го узла всей системы.

В правой части равенства (п.3.4) учтено, что реакция опоры F₁ приложена к первому узлу системы, второй узел свободен от внешних нагрузок, а внешнее усилие Р приложено к третьему узлу.

Теперь вводим граничные условия в перемещениях. Первый узел закреплен, а потому .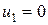

Остальные перемещения находим понижая порядок определителя матрицы жесткости. Это достигается замещением нулями первой строки и первого столбца и помещением в главную диагональ единицы:

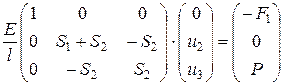
или

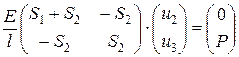
Умножая матрицы в левой части равенства, получаем равенство двух вектор столбцов:

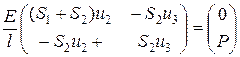
Отсюда следуют два равенства:

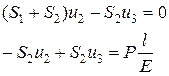(п.3.5)

Складывая оба равенства, получаем 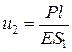. Подставляя это значение 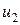во второе из равенств системы (п.3.5) и выполняя простейшие преобразования, находим: 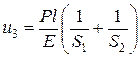. Окончательным решением поставленной задачи будут значения перемещений

; ;

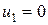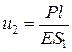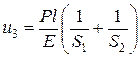
Ступенчатый стержень можно также рассматривать как систему из двух последовательно соединенных упругих элементов с жесткостям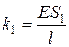и

и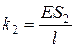

Тогда для состояния стержня можно составить матричное уравнение, с диагональной и симметричной матрицей жесткости, аналогичное тем, которые рассматривались в предыдущих примерах:

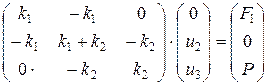
Перемещения u₂ и u₃ определяем заменой нулями первой строки и первого столбца и установкой единицы в первый диагональный элемент:

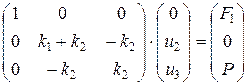
Откуда

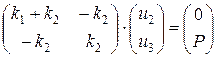
Решение этого матричного уравнения дает:

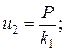
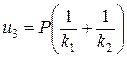
ример 4.

Для показанной на схеме системы пружин с жесткостью k₁, k₂,k₃ и k₄ построить глобальную матрицу жесткости.

Решение

Составим таблицу связи элементов и номеров узлов этих элементов:

Элемент	Узел i	Узел j

Поместим в таблицу матрицы жесткости для каждого элемента, указав при этом, в верхней строке перемещения каких узлов они связывают

u4 u1	u2 u3	u3 u5	u2 u1

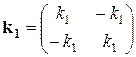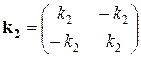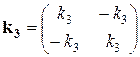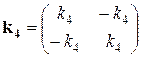Используя принцип суперпозиции, составим глобальную матрицу жесткости для всей системы элементов

u₁ u₂ u₃ u₄ u₅

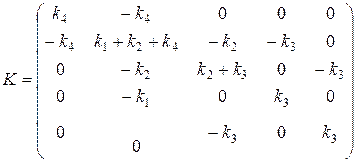
Полученная матрица является ленточной и симметричной. В рассмотренных примерах длина элементов отсутствует. Задача решена.

Задание к лабораторной работе

Вычислить:

• растяжение трех последовательно соединенных пружин жесткостью k₁ =5 кН/м, k₂=2кН/м и k₃=3кН/м. Система закреплена в первом (верхнем) узле и находится под действием силы Р₄=0,5 кН, направленной вдоль оси системы и приложенной в четвертом (нижнем) её узле. На узел 2 действует сила Р₂=0,2 кН, направленная вниз (по второму варианту направленная вверх). На третий узел силы не действуют. Собственный вес пружин считать пренебрежимо малым. Составить общую матрицу жесткости системы.

• Вычислить продольную деформацию двухступенчатой бетонной опоры, выполненной в виде цилиндра с длиной и площадью поперечного сечения нижней части l₁=0,5м, S₁=0,5м²,

с длиной и площадью поперечного сечения верней части l₁=0,3м, S₁=0,3м². На опору положен груз, создающий усилие 2 тонны силы. Модуль Юнга бетона Е=10гПа.