Алгоритм равномерного поиска
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции 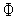 (
( 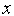 ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 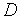 =[
=[ 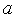 ,
, 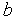 ],
],
Идея алгоритмов, относящихся к методу сокращения текущего интервала неопределенности, состоит в исключении в процессе поиска из рассмотрения тех подынтервалов, в которых в силу унимодальности функции 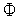 (
( 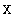 ) точка
) точка 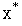 отсутствует.
отсутствует.
Текущий интервал неопределенности будем обозначать ТИН, а его длину |ТИН|. Так что, если 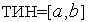 , то
, то 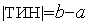 .
.
В алгоритме равномерного поиска испытания проводятся в точках, которые определяются путем равномерного деления интервала [ 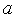 ,
, 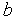 ] на
] на 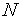 одинаковых подынтервалов. Из вычисленных значений функции
одинаковых подынтервалов. Из вычисленных значений функции 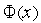 выбирается наименьшее. Пусть это значение достигается в точке
выбирается наименьшее. Пусть это значение достигается в точке 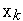 . Тогда в связи с унимодальностью функции
. Тогда в связи с унимодальностью функции 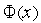 подынтервалы
подынтервалы 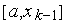 ,
, 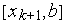 можно исключить из рассмотрения, т.е. сделать очередным интервалом неопределенности интервал
можно исключить из рассмотрения, т.е. сделать очередным интервалом неопределенности интервал 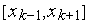 . Алгоритм относится к классу пассивных методов поиска.
. Алгоритм относится к классу пассивных методов поиска.
Более строго описанную схему алгоритма можно записать в нижеследующем виде.
1. Выполняем присваивания 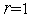 ,
, 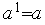 ,
, 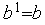 ,
, 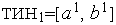 .
.
2. На текущем ТИН строим равномерную сетку с 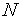 +1 узлами (см. рис. 1).
+1 узлами (см. рис. 1).
3. Вычисляем значения функции 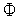 (
( 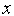 ) в узлах построенной сетки
) в узлах построенной сетки 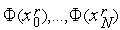 .
.
4. Находим минимальное из этих значений:
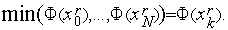
5. Выполняем присваивания 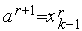 ,
, 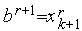 ,
, 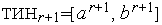 .
.
6. Если 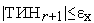 , то заканчиваем вычисления. Иначе - выполняем присваивание
, то заканчиваем вычисления. Иначе - выполняем присваивание 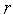 =
= 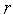 +1 и переходим на п.2. Здесь εx – требуемая точность решения.
+1 и переходим на п.2. Здесь εx – требуемая точность решения.
 |
Рис. 2. Построение сетки на текущем интервале неопределенности.
В качестве приближенного значения точки минимума 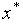 с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Первую итерацию приведенной схемы алгоритма равномерного поиска иллюстрирует рис. 3.
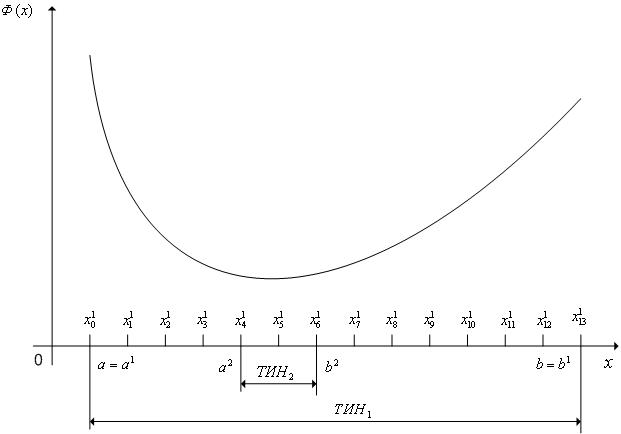 |
Рис. 3. Первая итерация поиск минимума одномерной унимодальной функции Ф(х) с помощью алгоритма равномерного поиска: N=13.
Легко видеть, что после одной итерации алгоритма равномерного поиска ТИН уменьшается в 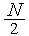 раз. Поэтому количество итераций
раз. Поэтому количество итераций 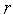 , необходимых для нахождения минимума функции с точностью εx, может быть найдено из условия
, необходимых для нахождения минимума функции с точностью εx, может быть найдено из условия
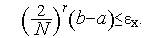
1.2. Метод деления интервала пополам Метод деления интервала пополам позволяет исключить в точности половину интервала на каждой итерации. Реализация метода основана на выборе трех пробных точек, равномерно распределенных на интервале неопределенности. Пусть I = b - а длина интервала неопределенности [а,b]. Разделим интервал [а,b] точками x1, xc и х2 на четыре равные части: хс = 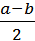 ; x1= ; x1= 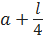 ; x2=b- ; x2=b- 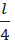 . . |
Вычисляются значения функции f( 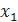 ), f(
), f( 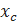 ) и f(x2). Сравниваются полученные значения и находится новый интервал неопределенности следующим образом:
) и f(x2). Сравниваются полученные значения и находится новый интервал неопределенности следующим образом:
1) если f(x1) < f(xc), то полагают b= хс. Средняя точка нового интервала хс = x1;
2) если f(x2) < f(xc), то полагают а = хс. Средняя точка нового интервала хс = х2;
3) если f(x1) = f(x2), то полагают а = x1, b = х2, хс — остается средней точкой нового интервала.
Затем снова вычисляют координаты х1 , х2 и продолжают поиск до выполнения условия b - а < s. За минимальное значение принимают х* = хс.
Метод дихотомии
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции 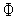 (
( 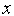 ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 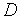 =[
=[ 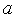 ,
, 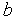 ],
],
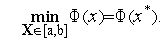
В алгоритм деления пополам или алгоритме равномерного дихотомического поиска испытания проводятся парами. Координаты каждой последующей пары испытаний разнесены между собой на величину 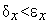 , где
, где 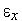 - требуемая точность решения. Испытания производятся в середине ТИН. По значениям
- требуемая точность решения. Испытания производятся в середине ТИН. По значениям 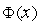 , полученным в этих точках, одна половина ТИН в силу унимодальности функции
, полученным в этих точках, одна половина ТИН в силу унимодальности функции 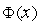 исключается из дальнейшего рассмотрения. Величина
исключается из дальнейшего рассмотрения. Величина 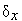 определяется требуемой точностью решения. Алгоритм относится к классу методов последовательного поиска.
определяется требуемой точностью решения. Алгоритм относится к классу методов последовательного поиска.
Более строго описанную схему алгоритма можно записать в нижеследующем виде.
1. Выполняем присваивания 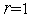 ,
, 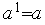 ,
, 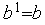 ,
, 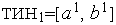 .
.
2. Вычисляем величины (см. рис. 1)
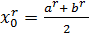 ;
; 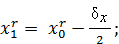
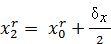 .
.
3. Вычисляем значения 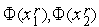 функции
функции 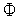 (
( 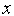 ).
).
4. Если 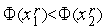 , то выполняем присваивания
, то выполняем присваивания 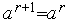 ,
, 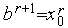 ,
, 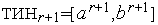 . Иначе - выполняем присваивания
. Иначе - выполняем присваивания 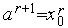 ,
, 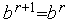 ,
, 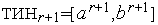
5. Если 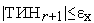 , то заканчиваем вычисления. Иначе - выполняем присваивание
, то заканчиваем вычисления. Иначе - выполняем присваивание 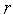 =
= 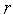 +1 и переходим на п.2.
+1 и переходим на п.2. 
 |
Рис. 4. К определению величин x0r,x1r,x2r.
В качестве приближенного значения точки минимума 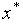 с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Приведенную схему алгоритма равномерного дихотомического поиска иллюстрирует рис. 5.
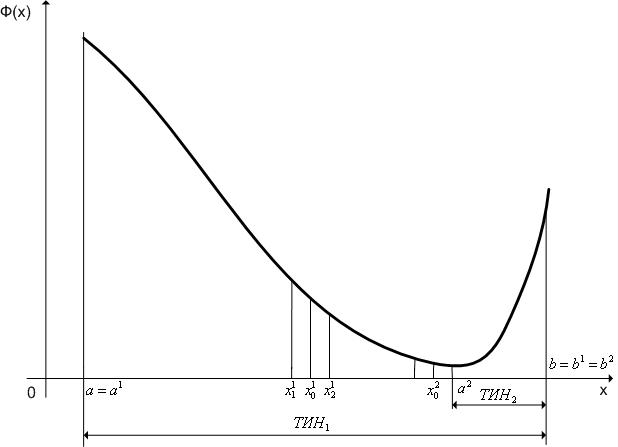 |
Рис. 5. Первые две итерации поиска минимума одномерной унимодальной функции с помощью алгоритма равномерного дихотомического поиска.
Легко видеть, что после одной итерации алгоритма равномерного поиска ТИН уменьшается в 2 раза. Поэтому количество итераций 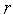 , необходимых для нахождения минимума функции с точностью εx, находится из условия
, необходимых для нахождения минимума функции с точностью εx, находится из условия
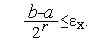
Метод золотого сечения
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции 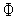 (
(  ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 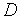 =[
=[ 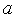 ,
, 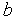 ],
],
 (
( 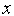 )=
)= 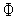 (
( 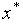 ).
).
