Нормальный (гауссовский) закон распределения. Кривая нормального распределения.

Если случайная величина X есть результат суммирования множества случайных величин с произвольными законами распределения, причем каждая из них играет примерно одинаковую роль в сумме, то закон распределения случайной величины X близок к закону распределения, называемому нормальным (гауссовским).

При нормальном (гауссовском) законе плотность распределения задаётся формулой:

,

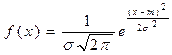где т - математическое ожидание случайной величины, σ -среднее квадратическое отклонение.

Вероятность попадания случайной величины на заданный участок

Вероятность попадания случайной величины в интервал (α;β) равна приращению её функции распределения на этом интервале:

P(a<X< β) = F(β) - F(a).

Если случайная величина подчинена нормальному закону, часто вместо её функции распределения применяется функция Лапласа.

Выражение

.

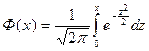называется функцией Лапласа. В справочниках функция Лапласа задана таблицей. Вероятность попадания нормальной случайной величины в интервал (α;β) определяется по формуле

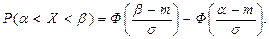
Значения функции Лапласа.

х	Ф(х)	х	Ф(х)	х	Ф(х)
0.0	0.0000	1.00	0.3413	2,0	0,4772
0.05		1.05		2.1
0.10		1.10		2.2
0.15		1.15		2.3
0.20		1.20		2.4
0.25		1.25		2.5
0.30		1.30		2.6
0.35		1.35		2.7
х	Ф(х)	х	Ф(х)	х	Ф(х)
0.40		1.40		2.8
0.45		1.45		2.9
0.50		1.50		3.0
0.55		1.55		3.1
0.60		1.60		3.2
0.65		1.65		3.3
0.70		1.70		3.4
0.75		1.75		3.5
0.80		1.80		4.0
0.85		1.85		4.5
0.90		1.90		5.0
0.95		1.95

Пример выполнения задания 1

У рабочего 20 однотипных деталей, из которых окрашено в красный цвет 9 деталей, в зеленый цвет 7 деталей и в синий 4 детали. Рабочий наудачу берет 6 деталей. Найти вероятность того, что среди выбранных деталей окажется 3 красных, 2 зеленых и 1 синяя.

Решение.

Обозначим буквой А то событие, вероятность которого требуется найти по условию задачи. Вероятность события равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

.

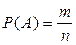Общее число возможных элементарных исходов п равно числу способов, которыми можно извлечь 6 деталей из 20, т.е. равно

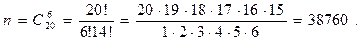
Число т исходов, благоприятствующих интересующему нас событию:

.

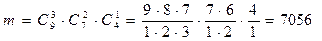Тогда: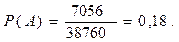

Пример выполнения задания 2

В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в твёрдом переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в твёрдом переплете.

Решение.

Введем обозначение событий. Обозначим буквой А то событие, вероятность которого надо найти:

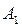- {первый взятый учебник имеет твёрдый переплет}.

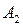- {второй взятый учебник имеет твёрдый переплет}.

Вероятность того, что первый учебник имеет твёрдый переплет, равна .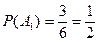

Вероятность того, что второй учебник имеет твёрдый переплет, при условии, что первый взятый учебник был в твёрдом переплете, т.е. условная вероятность события 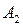, равна .

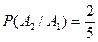Искомая вероятность того, что оба учебника имеют твёрдый переплет, по теореме умножения вероятностей зависимых событий равна

.

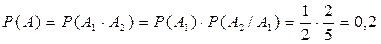Пример выполнения задания 3

В пирамиде установлены 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95. Для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?

Решение.

Обозначим события:

А – {стрелок поразил мишень}.

Гипотезы: 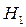- {стрелок взял для стрельбы винтовку с оптическим прицелом}; 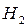- {стрелок взял для стрельбы винтовку без оптического прицела}.

Вероятности гипотез равны:

;

;

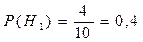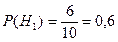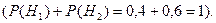
Условные вероятности гипотез соответственно равны:

;

.

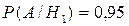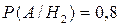Вероятность того, что стрелок поразил мишень из наудачу взятой винтовки, по формуле полной вероятности равна:

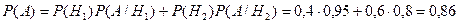
Вероятность того, что стрелок поразил мишень из винтовки с оптическим прицелом, по формуле Байеса равна:

.

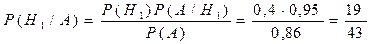Вероятность того, что стрелок поразил мишень из винтовки без оптического прицела, по формуле Байеса равна:

.

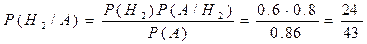Ответ: Вероятнее, что винтовка была без оптического прицела.

Пример выполнения задания 4

По цели производится 5 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,6. Для получения зачета по стрельбе требуется не менее трех попаданий. Найти вероятность получения зачета.

Решение:

Искомая вероятность находится по формуле

.

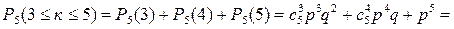
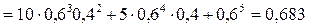Пример выполнения задания 5

Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,3; для второго – 0,4.

Для случайного числа попаданий в цель составить ряд и функцию распределения. Построить их графики. Найти M[x], D[x], σ[x].

Решение.

Случайная величина Х – число попаданий: X={0, 1, 2};

x=0 {никто не попал в мишень}:

;

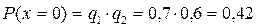х=1 {в мишень попал один стрелок}:

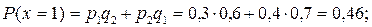
х=2 {в мишень попали оба стрелка}:

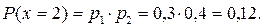
Ряд распределения:

Х
Р	0,42	0,46	0,12

Найдем функцию распределения:

х ≤ 0: F(х) = Р(x < 0) = 0;

0 < x ≤ 1: F(x) = P(x = 0) =0,42;

1< x ≤ 2: F(x) = P(x = 0) + P(x = 1) = 0,42+0,46=0,88;

x > 2: F(x) = P(x = 0) + P(x = 1) + P(x = 2) = 0,42+0,46+0,12 = 1.

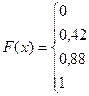
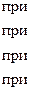
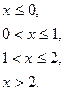
Многоугольник распределения имеет вид:

График функции F(х) имеет вид:

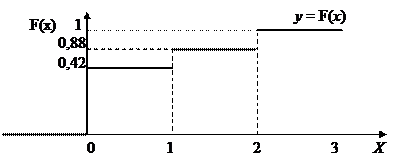
Математическое ожидание:

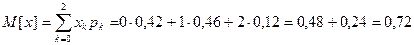
Дисперсия:

.

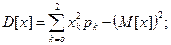
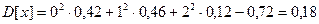Среднее квадратическое отклонение:

.

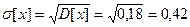Пример выполнения задания 6

Непрерывная случайная величина задана плотностью распределения:

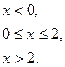
Требуется:

1) определить коэффициент с;

2) найти функцию распределения F(х);

3) построить графики f(х) и F(х);

4) найти вероятность того, что случайная величина Х принимает

значения из интервала (1; 2).

Решение.

1) Для определения коэффициента с используем свойство плотности распределения .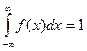

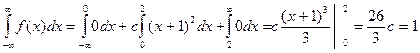. Получим: .

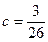2) Функцию распределения F(х) определяем по свойству плотности распределения

.

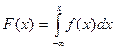а) случайная величина попадает на интервал (- ∞; 0):

.

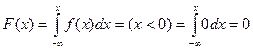б) случайная величина попадает на интервал (0; 2):

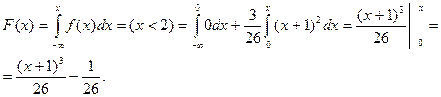
в) случайная величина попадает на интервал (2; +∞):

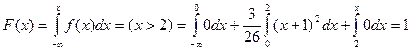
Таким образом,

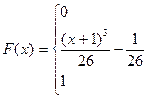
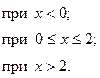
3) Графики функций f(х) и F(х):

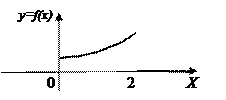4) Р(α<x<β) = F(β) - F(α).

P(1< x <2)=F(2) – F(1) = .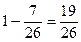

Пример выполнения задания 7

Случайная величина подчинена нормальному закону с параметрами т = 3 и σ = 2. Составить плотность распределения этой случайной величины f(х) и найти вероятность того, что случайная величина попадет в интервал (- 1; 4).

Решение.

Запишем плотность нормального распределения в общем виде:

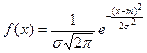, значит .

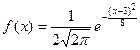Вероятность попадания нормально распределенной случайной величины Х в интервал (α; β) вычисляется по формуле:

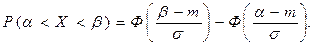
Следовательно,

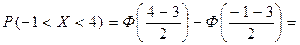
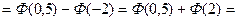0,1915 + 0,4772 = 0,6687.

Литература

1. Мохин-Блинов В.Н. «Элементы линейной алгебры и аналитической геометрии».

2. Мальцева С.Г., Мачехина Т.В. «Элементы векторной алгебры».

3. Бандурка В.А. «Методическое пособие по высшей математике».

4. Лісовська, Перестюк «Курс вищої математики».

5. Поплавська М.Г., Замятіна Є.М., Березнева С.М. «Збірник практичних робіт з вищої математики».

6. Ефимов Н.В.«Краткий курс аналитической геометрии».

7. Пискунов Н.С. «Дифференциальное и интегральное исчисление».

8. Мальцева С.Г. «Комплексные числа».

9. Письменный Д.Т. «Пределы».

10. Фисенко А.С.«Введение в математический анализ».

11. Коробский В.И.«Производная и дифференциал функции».

12. Фисенко А.С.«Дифференциальное исчисление функции одной переменной».

13. Фісенко А.С.«Інтегральне обчислення функцій однієї змінної».

14. Поплавская М.Г. «Дифференциальное исчисление функций нескольких переменных».

15. Мохин-Блинов В.Н. «Теория поля».

16. Мачехина Т.В., Ильенок Е.И., Бажанова В.Б. «Дифференциальные уравнения первого порядка».

17. Мачехина Т.В., Ильенок Е.И.«Дифференциальные уравнения высших порядков».

18. Мальцева С.Г., Сенчукова-Передерей М.Д. «Числовые и степенные ряды».

19. Мохин-Блинов В.Н., Фисенко А.С.«Операционное исчисление».

20. Саливон Ю.А. «Основные положения и задачи теории вероятностей и математической статистики».

Рекомендуемая литература

к модулю 1: [1], [2], [3], [4], [5].

к модулю 2: [3], [4], [5], [6].

к модулю 3: [3], [4], [7], [8], [9], [10], [11], [12].

к модулю 4: [7],[14].

к модулю 5: [7],[13].

к модулю 6: [7]

к модулю 7: [7], [16], [17].

к модулю 8: [7], [18]

к модулю 9: [19].

к модулю 10: [20].

СОДЕРЖАНИЕ

Предисловие
І СЕМЕСТР
Вопросы
Модуль 1. Линейная алгебра. Векторная алгебра
Модуль 2. Аналитическая геометрия
Модуль 3. Введение в математический анализ. Дифферен-циальное исчисление функций одной переменной
ІІ СЕМЕСТР
Вопросы
Модуль 4. Дифференциальное исчисление функций нескольких переменных
Модуль 5. Интегральное исчисление функций одной переменной
Модуль 6. Интегральное исчисление функций нескольких переменных
ІІІ СЕМЕСТР
Вопросы
Модуль 7. Дифференциальные уравнения
Модуль 8. Ряды
IV СЕМЕСТР
Вопросы
Модуль 9. Операционное исчисление
Модуль 10. Теория вероятностей
Литература
Рекомендованная литература

Светлана Михайловна БЕРЕЗНЕВА,

Людмила Павловна ТАРЛЕЦКАЯ,