Некоторые эталонные пределы
1. 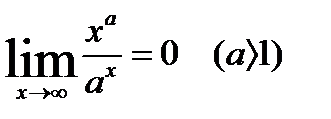 4.
4. 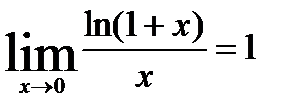
2. 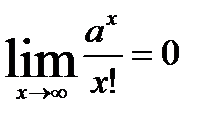 5.
5. 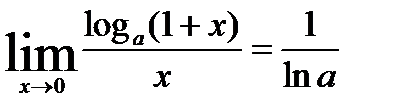
3. 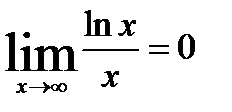 6.
6. 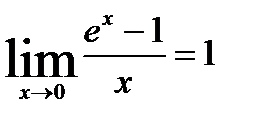
7. 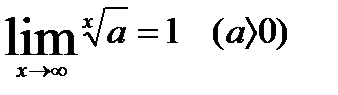 9.
9. 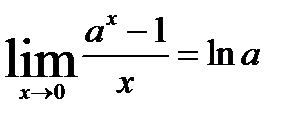
8. 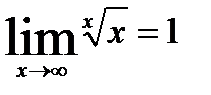 10.
10. 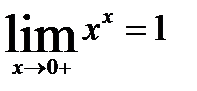
Нарушение ограничений, накладываемых на функцию при вычислении пределов, приводит к неопределённостям вида 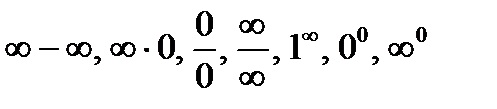 .
.
Элементарными приёмами раскрытия неопределённостей являются:
1) сокращение на множитель, создающий неопределённость;
2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при 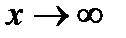 );
);
3) применение эквивалентных;
4) использование замечательных пределов.
Примеры. Найти пределы:
1. 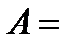
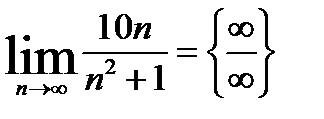 .
.
Разделим числитель и знаменатель дроби на 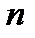 в старшей степени, т.е. на
в старшей степени, т.е. на 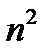 :
:
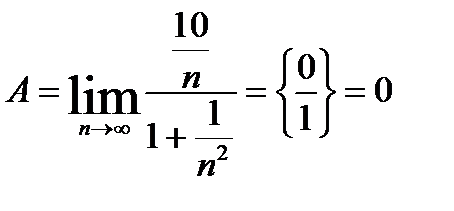 .
.
2. 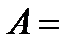
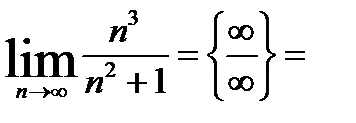
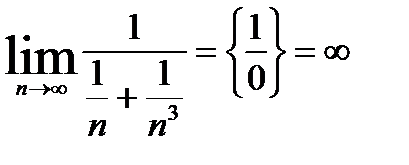 .
.
3. 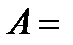
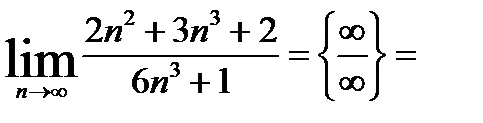
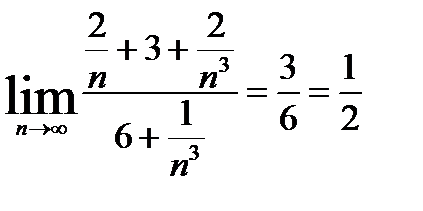 .
.
Таким образом,
если степень числителя меньше степени знаменателя, то предел равен 0;
если степень числителя больше степени знаменателя, то предел равен 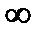 ;
;
если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при старших степенях.
4. 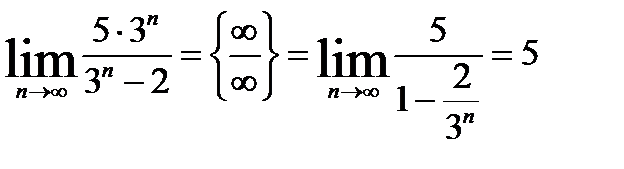 .
.
5. 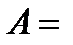
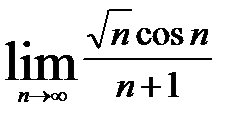 .
.
Последовательность 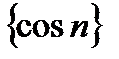 ограниченная, а последовательность
ограниченная, а последовательность 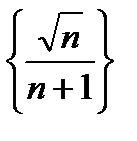 бесконечно малая, т.к. степень числителя меньше степени знаменателя. Значит,
бесконечно малая, т.к. степень числителя меньше степени знаменателя. Значит, 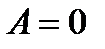 по теореме о произведении бесконечно малой на ограниченную.
по теореме о произведении бесконечно малой на ограниченную.
6. 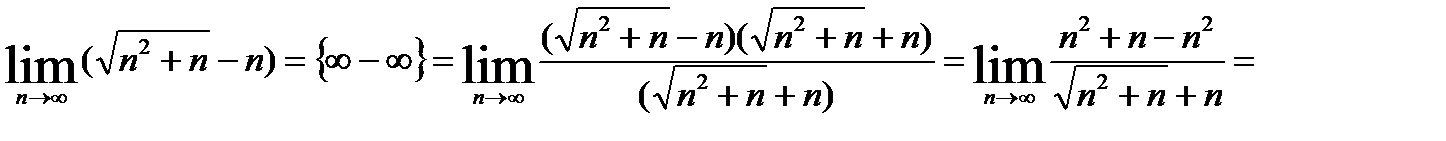
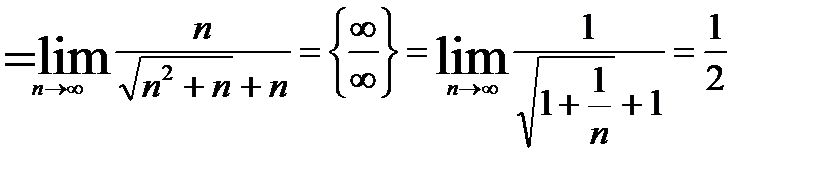 .
.
7. 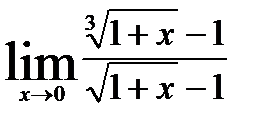 .
.
Ι способ. Здесь имеем неопределённость 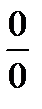 . Устраним неопределённость тождественным преобразованием – домножим числитель и знаменатель на сопряжённые выражения.
. Устраним неопределённость тождественным преобразованием – домножим числитель и знаменатель на сопряжённые выражения.
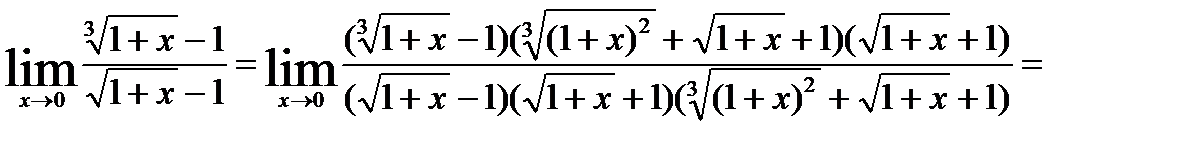
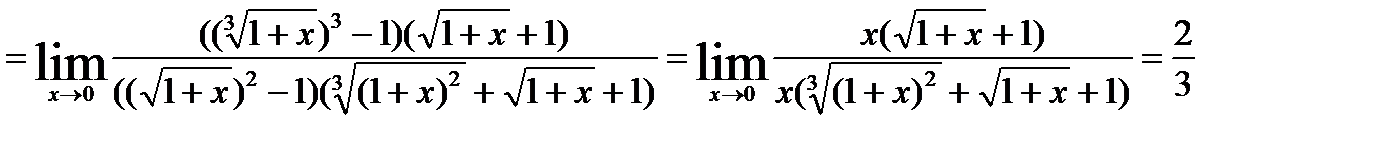 .
.
II способ. Положим 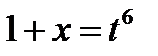 , тогда
, тогда 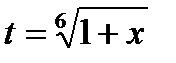 . Если
. Если 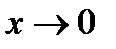 , то
, то 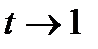 .
.
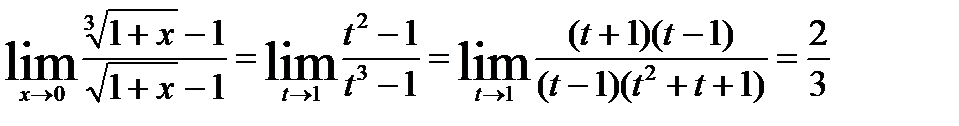 .
.
8. 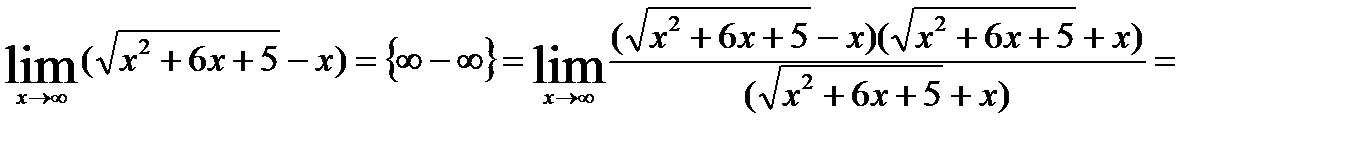
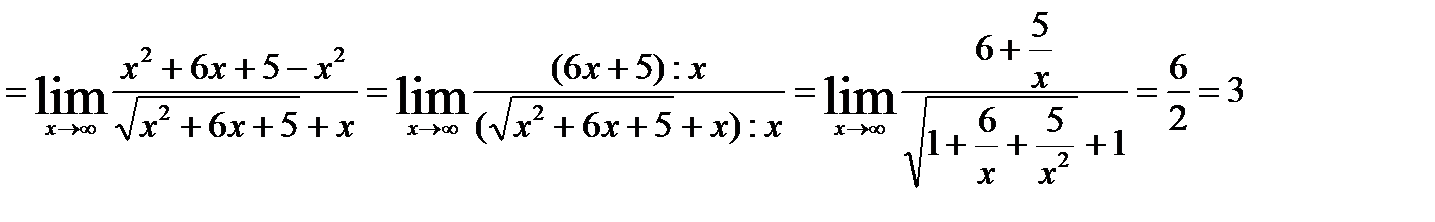 .
.
9. 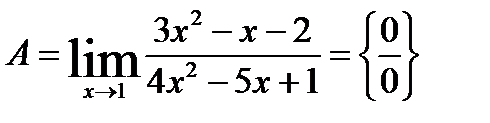 .
.
Разложим многочлены в числителе и знаменателе на множители
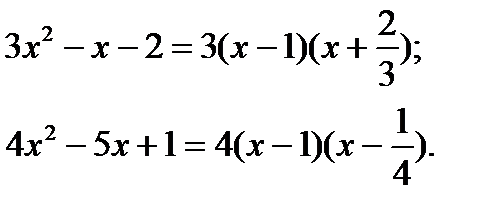
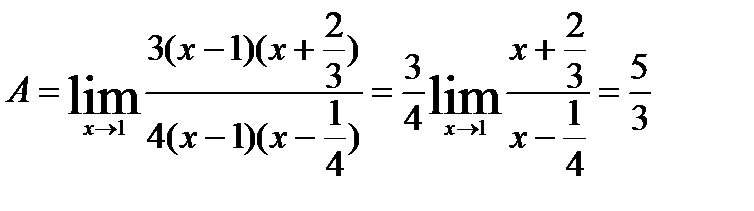 .
.
10. 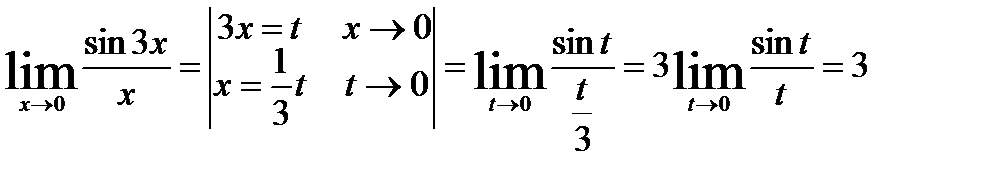 .
.
Иногда полезно воспользоваться формулами тригонометрии:
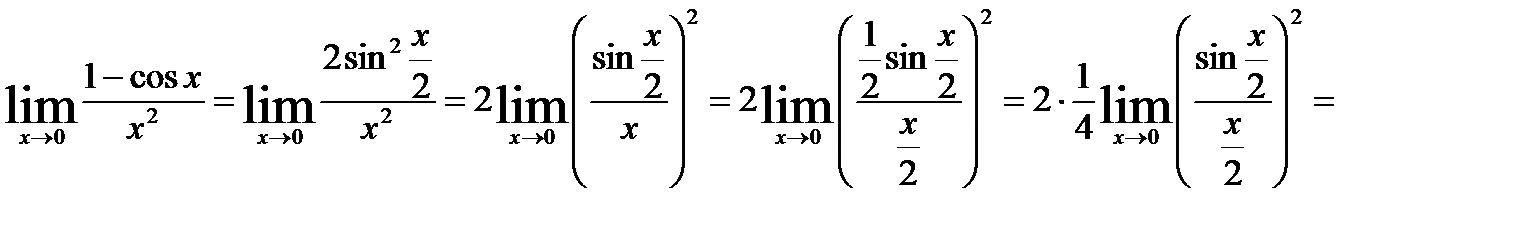 11.
11.
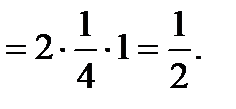
12. 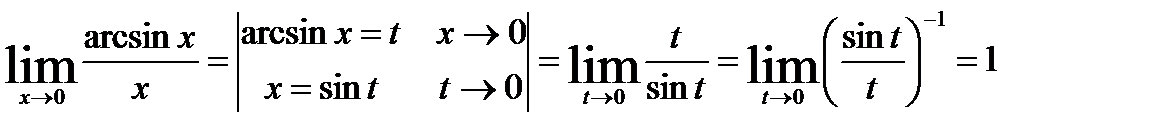 .
.
Заметим, что аналогично можно доказать:
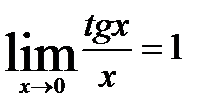 ;
;
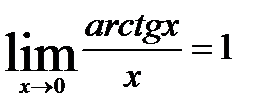 .
.
13. 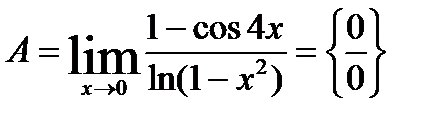 .
.
Для раскрытия неопределённости используем метод замены бесконечно малых эквивалентными:
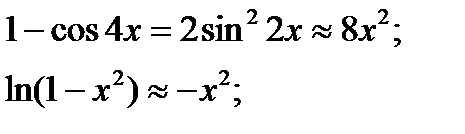
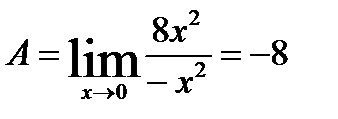 .
.
14. 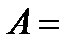
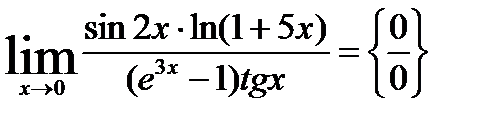 .
.
I способ. Имеющуюся неопределённость устраним тождественным преобразованием с последующим использованием замечательных пределов и теоремы о пределе произведения:
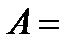
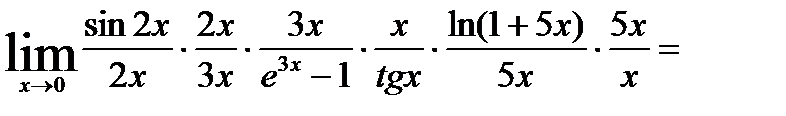
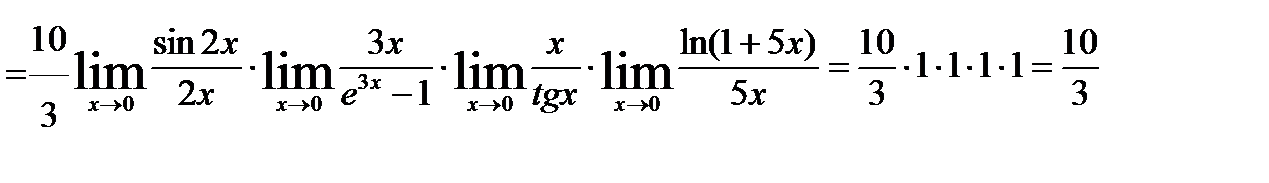 .
.
II способ. Так как при 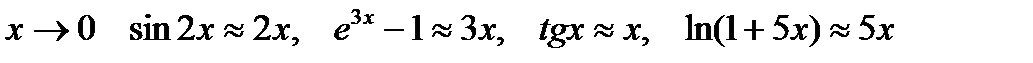 ,
,
то
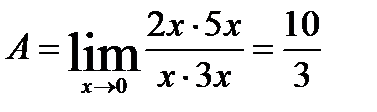 .
.
15. 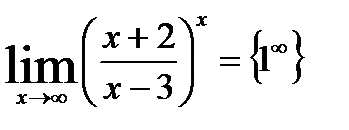 .
.
I способ. Имеющуюся неопределённость устраним тождественными преобразованиями с последующим использованием второго замечательного предела:
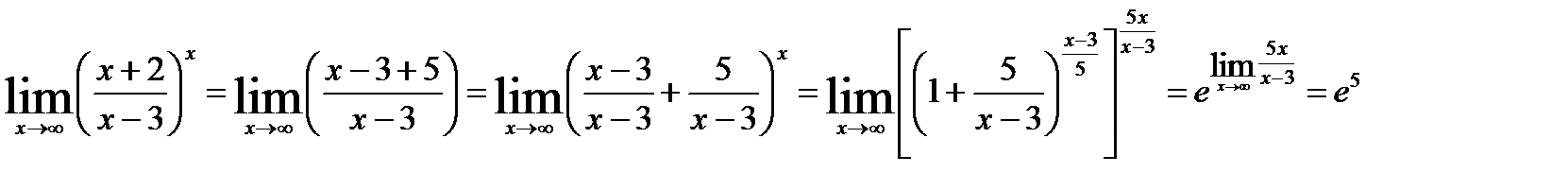 .
.
II способ. Используя тождество 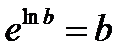 и непрерывность показательной функции, сведём неопределённость
и непрерывность показательной функции, сведём неопределённость 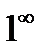 к неопределённости
к неопределённости 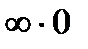 :
:
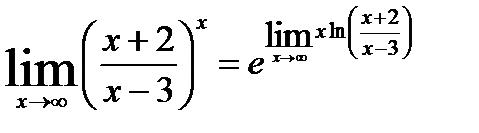 ;
;
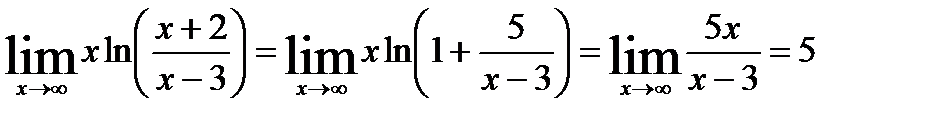 .
.
Таким образом, исходный предел равен 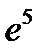 .
.
Непрерывность функции
Определение. Функция 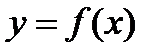 называется непрерывной в точке
называется непрерывной в точке 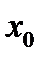 , если она определена в точке
, если она определена в точке 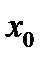 и в некоторой окрестности точки
и в некоторой окрестности точки 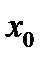 и если
и если 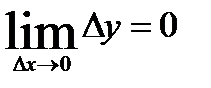 .
.
Геометрически непрерывность функции в данной точке означает, что разность ординат графика функции 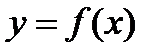 в точках
в точках 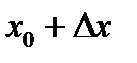 и
и 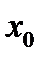 будет мала, если
будет мала, если 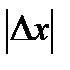 достаточно мало.
достаточно мало.
Определение. Если функция 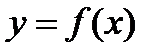 непрерывна в каждой точке интервала
непрерывна в каждой точке интервала 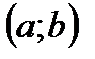 , то она непрерывна на этом интервале.
, то она непрерывна на этом интервале.
Если функция определена при 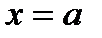 и при этом
и при этом 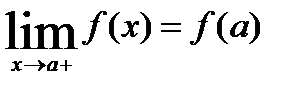 , то говорят, что функция
, то говорят, что функция 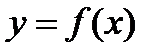 непрерывна в точке
непрерывна в точке 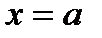 справа.
справа.
Если функция определена при 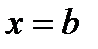 и при этом
и при этом 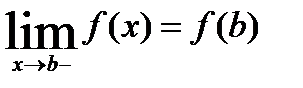 , то говорят, что функция
, то говорят, что функция 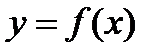 непрерывна в точке
непрерывна в точке 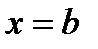 слева.
слева.
Если функция непрерывна на интервале 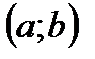 , и непрерывна в точках
, и непрерывна в точках 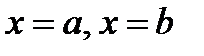 соответственно справа и слева, то функция непрерывна на отрезке
соответственно справа и слева, то функция непрерывна на отрезке 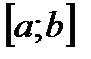 .
.
Если в точке 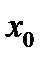 для функции
для функции 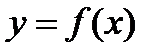 не выполняется какое-либо условие непрерывности, т.е. функция не определена в точке
не выполняется какое-либо условие непрерывности, т.е. функция не определена в точке 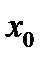 или не существует
или не существует 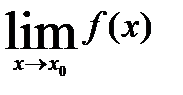 , или
, или 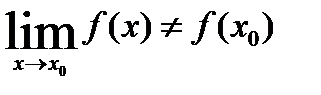 , то функция
, то функция 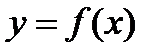 разрывна при
разрывна при 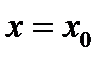 . Точка
. Точка 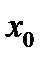 называется точкой разрыва.
называется точкой разрыва.
Теорема. Всякая элементарная функция непрерывна на своей области определения.
