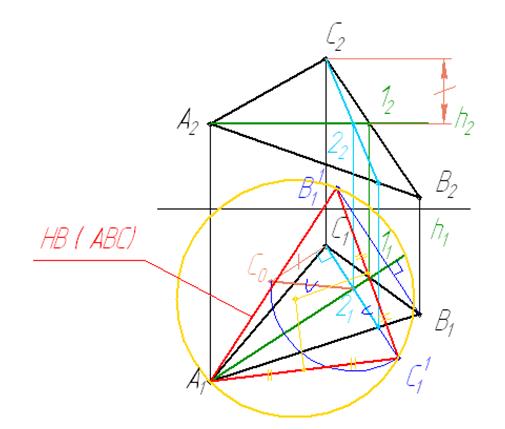
Исходные данные к задаче представлены в таблице 1. Способ вращения вокруг прямой уровня получил распространение при решении задач на определение натуральной величины плоских фигур
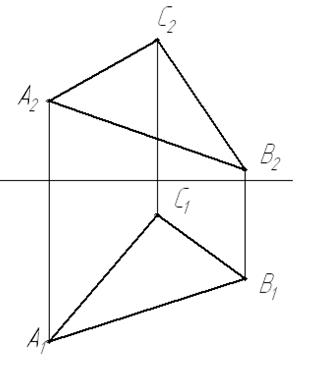
Рисунок 3
Решение:
Способ вращения вокруг прямой уровня получил распространение при решении задач на определение натуральной величины плоских фигур. В этом случае радиус вращения определяется линией ската (линией наибольшего наклона к плоскости). Натуральная величина радиуса вращения определяется способом построения прямоугольного треугольника.
При вращении вокруг прямой уровня все точки объекта двигаются в плоскостях, перпендикулярных оси вращения, а следовательно, их проекции будут двигаться по линиям, перпендикулярным проекции оси вращения.
Алгоритм решения задачи следующий:
1 Проводим горизонталь (или фронталь). Строим проекции линии ската.
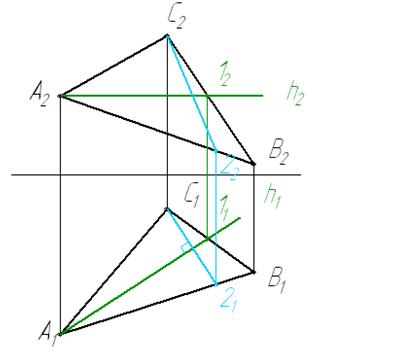
2 Находим натуральную величину линии ската – это и будет радиус вращения.
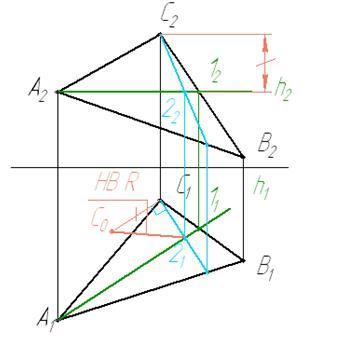
3 Проводим траектории движения точек. Откладываем на траектории радиус вращения и достраиваем недостающие точки треугольника. Получаем натуральную величину треугольника АВС.
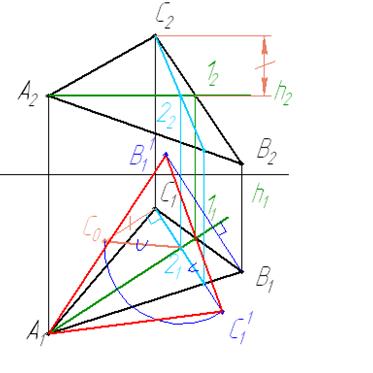
4 Находим центр описанной окружности как точку пересечения высот, проведенных в треугольнике. Строим окружность.