Замечание

а) || ||

б)

Пусть известны нормаль к плоскости и направляющий вектор прямой , тогда

а) || , (37)

б) || (38)

в) (39)

Глава III. Элементы математического анализа

§ 1. Кванторы

– «для любого » – квантор всеобщности,

– «существует такое, что …» – квантор существования,

– «существует только одно такое, что …» – квантор существования и единственности.

§ 2. Определение функций

Определение. Если каждому числу поставлено в соответствие по некоторому правилу вполне определенное действительное число , то говорят, что на множестве определена числовая функция , т.е. .

Множество называют областью определения функции и обозначают .

Определение. Если каждой паре значений двух независимых друг от друга величин и из некоторой области соответствует определенное значение величины , то говорят, что есть функция двух независимых переменных и , определенная в области , т.е.

Область при этом называется областью определения функции .

При нахождении области определения функции двух переменных следует учитывать свойства элементарных функций.

	Функция	Область определения
1.
2.
3.
4.
5.
6.
7.
8.

§ 3. Предел функции , непрерывность, точки разрыва

Рассмотрим

– « »–окрестность точки ,

– выколотую « »– окрестность точки .

Определение (по Коши):Число называется пределом функции в точке (или при ), если для любого существует такое число , что для всех , удовлетворяющих условию выполняется неравенство: .

.

– Первый замечательный предел

(40)

– Второй замечательный предел

Таблица эквивалентностей при

, , , , , , ,

К неопределенностям относятся выражения вида , , , , и др.

1. . Чтобы раскрыть неопределенность этого вида необходимо в числителе и знаменателе дроби выделить сомножитель, обращающий их в ноль и сократить на него дробь. Способы выделения сомножителя зависят от вида функции, например,

а)

б)

Можно также пользоваться таблицей эквивалентностей.

в)

2. . Чтобы раскрыть неопределенность вида можно пользоваться эквивалентными бесконечно большими, например,

3. Неопределенности вида и сводятся предварительно к неопределенностям вида или , например,

а)

б)

4. Неопределенность вида раскрывается с помощью второго замечательного предела. Например,

.

Определение.Функцию называют непрерывной в точке , если выполняются следующие три условия:

1) определена в точке , то есть

2) существует ,

3)

1. Если в точке существуют конечные односторонние пределы и или , то точку называют точкой разрыва I рода, устранимого.

2. Если в точке существуют конечные односторонние пределы и , то точку называют точкой разрыва I-го рода, неустранимого.

3. Если хотя бы один из односторонних пределов равен или , то точку называют точкой разрыва II рода.

Пример:

В точке функция не определена, следовательно, – точка разрыва.

,

Следовательно, точка разрыва II рода.

§ 4. Производная функции одной переменной

Определение. Производной функции в точке называют предел отношения приращения функции в этой точке к приращению аргумента, когда приращение аргумента стремится к 0 (при условии, что этот предел существует)

Геометрически производная определяет угловой коэффициент касательной к графику в точке .

Уравнение касательной к кривой:

, (41)

уравнение нормали к кривой:

, если (42)

Физический смысл: характеризует мгновенную скорость изменения функции при .

Таблица производных

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Правила дифференцирования

1.

2.

3.

4.

5.

6.

7.

8.

(43)

9.

(44)

Правило Лопиталя

Теорема (Лопиталя). Если функции и :

1) дифференцируемы в некоторой окрестности точки , за исключением, быть может, самой точки ,

2) при одновременно являются бесконечно малыми или бесконечно большими,

3) в этой окрестности,

4) существует предел отношения производных (конечный или бесконечный), то существует и предел , причем справедлива формула

(45)

§ 5. План полного исследования функции:

I.Область определения и область непрерывности:

1) если есть точки разрыва, установить их характер, найдя пределы слева и справа;

2) выяснить, не является ли функция четной (график симметричен относительно ) или нечетной (график симметричен относительно начала координат), периодической;

3) точки пересечения с осями координат.

II.Асимптоты.

Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к 0 (Точка удаляется в бесконечность, если ее расстояние от начала координат неограниченно увеличивается).

Прямую называют вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .

Прямую называют наклонной асимптотой графика функции при , если функцию можно представить в виде:

где при

В этом случае

, (46)

В частности, если функция стремится к конечному пределу при : , то, очевидно, и линия имеет горизонтальную асимптоту, параллельную оси , именно .

III.Точки экстремума, интервалы возрастания и убывания.

Теорема(Достаточный признак монотонности)

Если на некотором промежутке имеет производную для , то на функция возрастает (убывает ).

Теорема (Необходимое условие экстремума)

Если дифференцируема в точке и имеет в этой точке экстремум, то .

Функция может иметь экстремум среди точек, в которых:

1) ,

2) ,

3) – не существует, где .

Точки всех этих типов – критические точки функции.

Теорема(Достаточное условие экстремума)

Пусть дифференцируема в (кроме, быть может, самой точки ). Если – критическая точка и производная при переходе через точку меняет знак, то функция имеет в данной точке экстремум:

максимум, если знак производной меняется с «+» на «–»,

минимум, если знак производной меняется с «–» на «+».

IV.Точки перегиба, интервалы выпуклости и вогнутости.

Определение. Кривую называют вогнутой в точке , если существует такая окрестность точки , в которой кривая расположена над касательной, проведенной к ней в точке (рис. 5).

Определение. Кривую называют выпуклой в точке , если существует такая окрестность точки , в которой кривая расположена под касательной, проведенной к ней в точке (рис. 6).

Теорема (Достаточное условие выпуклости (вогнутости))

Если во всех точках : , то кривая на этом интервале выпукла (вогнута).

Определение. Точку, отделяющую выпуклую часть непрерывной кривой от вогнутой, называют точкой перегиба кривой.

Теорема (Достаточное условие перегиба)

Если или не существует и при переходе через меняет знак, то точка кривой с абсциссой будет точкой перегиба.

V.Построение графика.

§ 6. Частные производные функции нескольких переменных.

Производная сложной функции нескольких переменных

Определение. Частной производной функции по переменной в точке называется предел отношения частного приращения функции по к приращению по при неограниченном убывании последнего к нулю:

Другое обозначение: .

Таким образом, частная производная функции по переменной вычисляется в предположении, что значение постоянно.

Аналогично:

Другое обозначение: .

Частная производная функции по переменной вычисляется в предположении, что значение постоянно.

Частные производные функции сами являются функциями этих же переменных и могут иметь производные, которые называются частными производными второго порядка.

Пусть дана функция , где ; .

Тогда ,

. (см. рис. 7)

Если , а , , то

(см. рис. 8)

§ 7. Наибольшее и наименьшее значения функции

Наибольшее или наименьшее из всех значений нельзя смешивать с максимумом или минимумом функции, которые являются наибольшим или наименьшим значением функции только по сравнению с ее значениями в соседних точках.

Функция , непрерывная в некоторой ограниченной замкнутой области , обязательно имеет в этой области наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри области , или в точках, лежащих на границе области.

Чтобы найти наибольшее или наименьшее значения функции в ограниченной замкнутой области , где она непрерывна, можно руководствоваться следующим правилом:

1. Найти критические точки, лежащие внутри области и вычислить значения функции в этих точках.

2. Найти наибольшее или наименьшее значения функции на границе области .

3. Сравнить полученные значения функции: самое большее из них и будет наибольшим, самое меньшее – наименьшим значением функции в области .

§ 8. Неопределенный интеграл

Определение. Функция называется первообразной функции на множестве , если для любого выполняется равенство .

Определение. Множество всех первообразных функций для называется неопределенным интегралом от функции и обозначается символом .

Т.е.

Таблица интегралов

1. .
2. ,
3. ,
4. ,
5. ,
6. ,
7. ,
8. ,
9. ,
10. ,
11. ,
12. ,
13. ,
14. .

Метод замены переменной

Метод замены переменной состоит в том, что в интеграл , нахождение которого затруднительно, вводят новую переменную , связанную с переменной соотношением

,

где – непрерывная монотонная функция, имеющая непрерывную производную на некотором интервале изменения .

Таким образом,

После того, как интеграл найден, возвращаются к первоначальной переменной с помощью подстановки .

Пример:

.

Метод интегрирования по частям

Интегрирования по частям основано на применении формулы

(47)

Случаи применения формулы по частям.

I. ; ; ; .

II. ; ; ; ; .

За , ,

,

,

,

.

III. , .

Применяется двукратное интегрирование по частям.

Пример:

.

Интегрирование рациональных функций

Найдем интегралы от простейших рациональных дробей:

1. .

2. .

3. ,

где , т.е. квадратный трехчлен не имеет действительных корней.

.

Пример:

Интегрирование выражений, содержащих тригонометрические функции

1. Интегралы вида: .

а) Если и нечетное, то подстановка приводит к интегралу от рациональной функции.

Если и нечетное, то к тому же приводит подстановка .

б) Если оба показателя и положительные и четные, то применяются формулы:

(48)

в) Если оба показателя и отрицательные и сумма их четная, то подстановка приводит к интегралу от рациональной функции.

При этом , , .

2. Интегралы вида:

путем подстановки сводится к интегралу от рациональной функции, при этом .

3. Интегралы вида:Формулы:

: ,

: ,

: ,

Примеры:

1.

.

2.

.

3.

.

§ 9. Определенный интеграл

Если на , то определенный интеграл представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями (рис. 9).

Формула Ньютона-Лейбница:

,

где – первообразная для .

Интегрирование по частям:

, (49)

где – дифференцируемые функции на .

Замена переменной:

,

где – функция непрерывная вместе со своей производной на отрезке – функция непрерывная на .

Если – нечетная функция, то .

Если – четная функция, то .

§ 10. Приложения определенных интегралов

1) Площадь криволинейной трапеции, ограниченной графиком функции , прямыми и осью вычисляется по формуле

2) Площадь плоской фигуры, ограниченной графиками функций

и прямыми

вычисляется по формуле:

(рис. 10) (50)

3) В полярных координатах площадь криволинейного сектора , ограниченного кривой и лучами вычисляется по формуле:

(рис. 11) (51)

4) Если тело образовано вращением вокруг оси криволинейной трапеции, то его объем

(52)

5) При вращении вокруг оси криволинейной трапеции, образуется тело вращения, объем которого

(52')

6) Если плоская кривая задана уравнением , то длина ее дуги от точки до точки вычисляется по формуле:

(53)

Если задана параметрически:

, где , то длина ее дуги вычисляется по формуле:

(54)

Если задана в полярных координатах уравнением , то длина ее дуги определяется по формуле:

(55)

7) Работа переменной силы , где – непрерывная функция на , действующей в направлении оси на отрезке вычисляется по формуле:

8) Если материальная точка движется прямолинейно со скоростью , то пройденный ею за промежуток времени от до путь .

Глава IV. Пример решения варианта контрольной работы

Задача № 1. Вычислить определители :

.

Решение: По правилу вычисления определителя 2-го порядка:

По правилу треугольников:

Ответ: .

Задача № 2. Решить систему двумя способами

а) методом Гаусса;

б) по формулам Крамера, где – матрица из задачи №1,

Решение:

Имеем:

а) Переставим местами два первых уравнения

Составим расширенную матрицу системы

Первую строку умножим на «–2» и сложим со второй строкой.

Первую строку умножим на «–6» и сложим с третьей строкой.

Получаем матрицу:

.

Переставим местами II и III уравнения:

. Разделим II-ю строку на 17:

.

Умножим II-ю строку на «–6» и сложим ее с III строкой:

.

Этой матрице соответствует система уравнений:

б) по формулам Крамера:

.

Тогда: .

Ответ: .

Задача № 3. Вычислить величину момента силы , приложенной к точке относительно точки , если .

.

Решение:

Момент силы равен векторному произведению вектора на вектор , т.е. по формуле (8) имеем:

Так как

имеем

Ответ: .

Задача № 4. Даны координаты вершин пирамиды .

Найти: а) площадь грани

б) объем пирамиды.

Решение:

а) Воспользуемся формулой (10):

Тогда площадь грани равна половине площади параллелограмма, построенного на векторах и , т.е.

б) Воспользуемся формулой (11):

.

Ответ: , .

Задача № 5. Дано уравнение прямой. Записать его в следующих видах:

1. Уравнение в отрезках.

2. Уравнение с угловым коэффициентом.

Построить прямую в системе координат.

.

Решение:

1. По формуле (14):

2. По формуле (13):

Имеем , т.е.

Построим прямую или

Ответ: 1.

2.

Задача № 6. Даны координаты вершин треугольника . Найти:

1.

y

Уравнение стороны .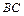

2.

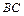1

A

Длину стороны .