Смешанное включение приемников электрической энергии

При смешанном соединении при­емников (рис. 7) рассмат­ривают вначале участок с па­раллельным соединением со­противлений R₂ и R₃, заменяют этот участок эквивалент­ным: 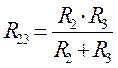с напряжением на этом участке U₂₃ и рассматривают в дальнейшем эту цепь как цепь с последовательным соединением R₁ и R₂₃ (рис. 8).

R_Э = R₁+R₂₃ = R₁+ 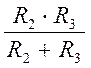. (2.11)

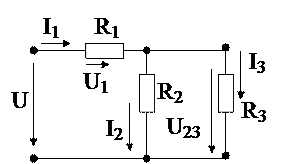Рисунок 7 – Смешанное соединение приемников постоянного тока

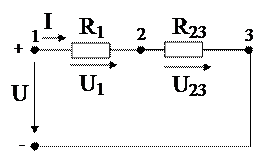Рисунок 8 – Эквивалентная схема цепи (рис. 7) после преобразования параллельного участка

В соответствии с законами Кирхгофа для цепи (см. рис. 7) I =I₁+I₂ и U = U₁+U₂₃.

На участке 2-3 ток I₁ делится на токи I₂ и I₃ : I₂ = 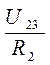; I₃= .

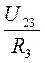Принимая во внимание закон Ома для этого же участка U₂₃ = I₁ · R₂₃ = 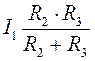, получают I₂= 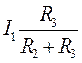и I₃= .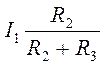

Говорят, что ток делится в двух параллельных ветвях прямо пропорцио­нально сопротивлению смежной ветви.

Сложные разветвленные электрические цепи анализируются с помощью уравнений, составленных по законам Кирхгофа. Если электрическая цепь имеет n ветвей и y узлов, то необходимо иметь n независимых уравнений, из которых y-1 уравнений составляют по I закону Кирхгофа. До­полнительные уравнения, число которых равно n-(у-1), составляют по II закону Кирхгофа для независимых контуров цепи. Независимым (или фундаментальным) контуром называется такой, в который входит хотя бы одна независимая ветвь, т.е. ветвь, не входящая в дру­гие контуры.

В простых цепях выбор независимых контуров трудностей обычно не вызы­вает, однако в цепях с большим количеством ветвей и узлов целесооб­разно пользоваться методом графов.

Граф электрической схемы – совокупность всех ветвей и узлов расчетной цепи без указания элементов (скелет цепи).

Дерево граф – совокупность ветвей графа, касающихся всех узлов, но не образующих ни одного замкнутого контура.

Корень графа – узел, из которого строится дерево графа.

В качестве примера рассмотрим сложную электрическую цепь, ске­летная схема которой дана на рисунке 9. На скелетной схеме цепи изоб­ражаются только узлы и ветви цепи.

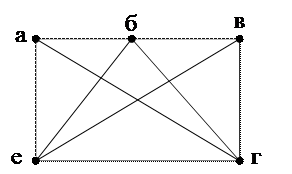
Рисунок 9­ – Граф электрической цепи (скелетная схема)

На рисунке 10 приведено дерево графа этой цепи с корнем в узле «е» (дерево выделено жирными линиями). Для графа одной и той же цепи можно построить несколько деревьев, принимая за корень дерева различные узлы. Ветви графа, не вошедшие в дерево, называются хордами (на рис. 10 изображены тонкими линиями). Число независимых кон­туров в цепи равно числу хорд графа, а сам независимый контур состоит только из одной хорды.

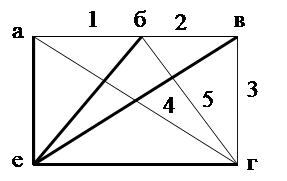Рисунок 10 – Дерево графа с корнем в узле «е» и пятью независимыми контурами