Из появившегося окна математической палитры вызвать мат-

ричную и векторную палитру. Для этого щелкнуть мышью по .

Вызов шаблона матрицы и её ввод

1. Из окна матричной палитры вызвать панель ввода матрицы. Для этого щелкнуть мышью по .

2. Указать размеры матрицы в соответствующих местах открыв- шейся панели и щелкнуть ОК.

Набрать матрицу, передвигаясь стрелками. После набора последнего числа нажать клавишу ПРОБЕЛ.

3.1.1 Вычисление определителя

1. Активизировать мышью пункт SIMBOLICS в верхней строке.

Указать мышью на MATRIX, затем справа на DETERMINANT и нажать левую кнопку мыши. На этом шаге появится ответ.

3.1.2. Обращение матрицы

Проделать то же, что при вычислении определителя, но в конце указать справа на INVERT.

3.1.3. Решение систем линейных уравнений

1. Набрать А:= и вызвать ввод матрицы, указать размеры и ввести матрицу системы ( без свободных членов ).

2. Набрать В:= и ввести матрицу-столбец свободных членов.

3. Набрать x:=lsolve(A,B) и нажать Enter.

4. Набрать х:= и на экране появится решение системы.

3.1.4. Выполнение алгебраических действий над матрицами

1. Обозначить разными буквами матрицы, из которых составлено

выражение, которое требуется вычислить, и поочередно ввести

эти матрицы и присвоить соответствующим буквам их значения.

2. Набрать Х:= и далее набрать данное алгебраическое выражение. Нажать Enter.

3. Набрать Х:= и на экране появится результат.

Например, если требуется вычислить 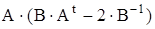, то нуж- но сначала ввести матрицы А и В и затем набрать: , нажать Enter, набрать Х:= и появится ответ.

Решение квадратных уравнений

1. Набрать В:= и ввести матрицу-столбец коэффициентов уравнения по порядку сверху, начиная со свободного члена, и нажать Enter.

2. Набрать х:=polyroots(B) и нажать Enter.

Набрать х:= и появятся корни.

3.1.6. Операции над матрицами с параметрами

Вычисление определителя.

1. Набрать А(р):= и ввести матрицу с коэффициентами, содержащими параметр р. Нажать Enter.

2. Набрать f(p):= A(p) и нажать Enter.

3. Набрать f(p):® и появится выражение для определителя.

Общее решение неопределённой системы.

Если обратиться обычным образом к MATHCAD-у за решением

с неопределённой системой, то он даст одно из решений. Поэтому, если мы хотим получить общее решение, нужно провести предварительное исследование системы, найти ранг, выделить базисный минор, отбросить лишние уравнения, выделить главные и свободные неизвестные. Рассмотрим на примере, разобранном в 4.5. На том шаге, когда обнулилась 4-я строка матрицы, стало ясно, что можно взять первые 3 уравнения, а 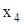объявить свободной неизвестной. Вводим параметр р = 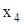и находим неизвестные 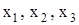, решая систему

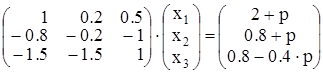
Теперь, чтобы получить общее решение нужно сделать:

1. Набрать А:= и ввести матрицу системы.

2. Набрать В(р):= и ввести столбец свободных членов.

3. Набрать .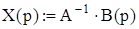

4. Набрать Х(р):® и появится ответ.

Использование АРММ

Через 1-й пункт: ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ из МЕНЮ ПРОГРАММ войти в подменю ЛИНЕЙНАЯ АЛГЕБРАи обращать-

ся к подпрограммам: ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МЕТОДОМ ГАУССА, ОБРАЩЕНИЕ МАТРИЦ МЕТОДОМ ГАУССА, РЕШЕНИЕ

СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КВАДРАТНОГО КО-

РНЯ, ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТО-

ДОМ ГАУССА. Все необходимые инструкции по их использова-

нию появляются на экране в процессе работы.

4. УКАЗАНИЯ К РЕШЕНИЮ

НАИБОЛЕЕ СЛОЖНЫХ ЗАДАНИЙ

4.1. Пример выполнения задания 2.4

Пусть требуется найти определитель:

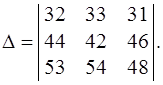
Поступим следующим образом: Сначала уменьшим элементы

матрицы, используя то свойство определителя, которое утверж-

дает, что он не меняется при вычитании из одной строки (или

столбца) другой строки ( или столбца ), умноженной на некото-

рое число. Для этого вычтем из второго столбца первый и из

третьего тоже первый. Получим

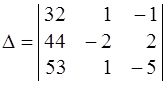. К 3-му столбцу прибавим 2-й: .

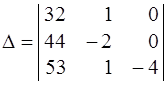Так как в 3-м столбце стоят 2 нуля, то вычисления упрощаются,

если разложить определитель по 3-му столбцу.

Получаем: 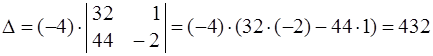. Проверить вычисления можно путем вычисления D на ЭВМ ( см.раздел 3 ).

4.2. Пример выполнения задания 2.11

Пусть требуется решить матричное уравнение

.

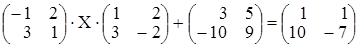Перенесём матрицу 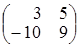в правую часть и вычтем из матрицы

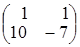. Получим 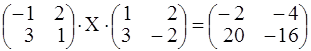. Умножим

полученное равенство слева на 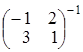и справа на .

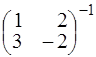Получим 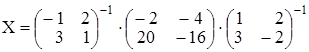. Далее, находим обрат-

ные матрицы ; .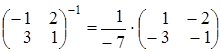

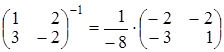Подставим в выражение для Х:

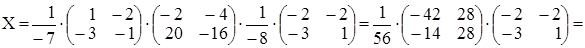
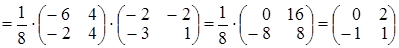. Проверим подстанов-

кой матрицы Х в исходное уравнение

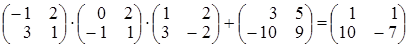. Вычисляем

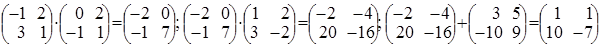
4.3. Пример выполнения задания 2.12

Пусть требуется решить уравнение .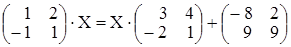

Обозначим элементы неизвестной матрицы 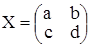и выполним

действия. В левой части равенства получим

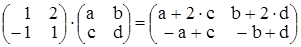. А в правой -

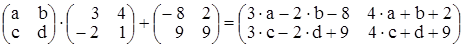. Приравнивая

соответствующие элементы матриц в левой и правой частях, полу-чим систему уравнений

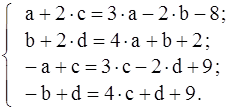
Переносим неизвестные в левую часть и приводим подобные члены:

.

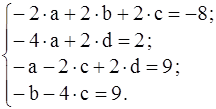Для решения системы можно обратиться к ЭВМ (см. раздел 3) или решить вручную. Выражаем d через a из 2-го уравнения и b через c из 4-го уравнения d = 1+2×a , b = - 9 - 4×c, и подставляем в 1-е и 3-е уравнения

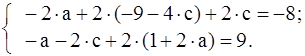
Сокращаем 1-е уравнение на 2 и приводим подобные члены

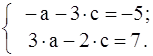
Прибавляя ко 2-му уравнению 1-е, умноженное на 3, получаем

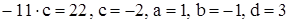. Получили искомую матрицу

.

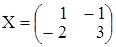Проверяем ответ подстановкой в матричное уравнение

.

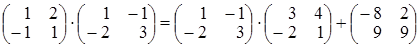Выполняя действия, получаем и в левой и в правой части одну

и ту же матрицу

.

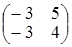4.4. Пример выполнения задания 2.13

Пусть нам дана система

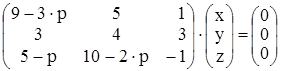. Так как система однородная, то для

того, чтобы она имела ненулевые решения, необходимо, чтобы её

определитель 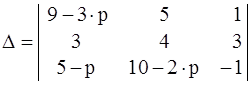был равен нулю.

Найдём такие значения р, при которых функция D(р) обращается в нуль. Найдём выражение для D(р), раскрывая определитель по пер-вой строке ( на этом этапе можно обратиться к ЭВМ, см. раздел 3.3)

= .

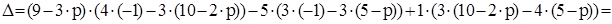
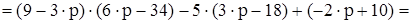
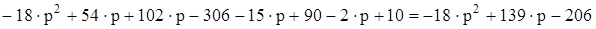Получаем квадратное уравнение: .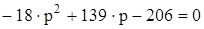

( Для его решения можно обратиться к ЭВМ ). Находим его корни

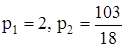. Далее находим для каждого р соответствующие ре-

шения системы ( это можно также проделать на ЭВМ ).

1. 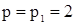. Получается система

.

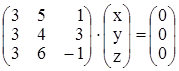Ищем общее решение этой системы ( она должна быть неопределённой ) методом Гаусса. При этом столбец свободных членов всегда будет нулевым и его можно не писать.

Приводим матрицу системы к стандартному ступенчатому виду

.

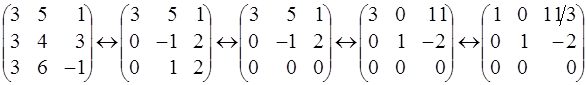Записываем систему, соответствующую последней матрице

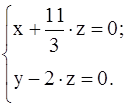
Получилось, что x, y – главные неизвестные; z – свободная неизвестная. Возьмём z = 1, тогда 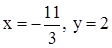. Нашли решение

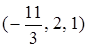, однако оно пока не удовлетворяет условию .

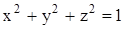Но так как наша система – однородная, то при умножении реше-ния на какое-либо число получается тоже одно из решений этой систе-мы. Тогда умножим полученное решение на такое число k, чтобы условие 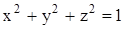было выполнено. Можно проверить подста-новкой, что можно взять 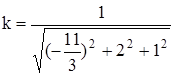. Для р = 2 получаем требуемое решение:

.

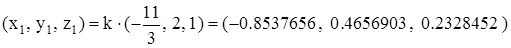2. 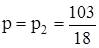. Получается система

.

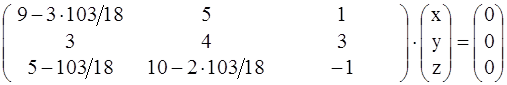Ясно, что как и в случае р = 2, третье уравнение будет следствием первых двух и его можно отбросить. Система получается неопределённая и можно взять х = 1. Найдём у и z

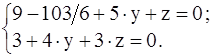
( Для решения можно обратиться к ЭВМ ). Вычтем из 2-го уравнения 1-е, умноженное на 3

.

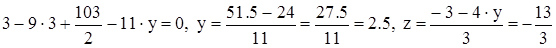Находим второе решение так же, как для р = 2

.
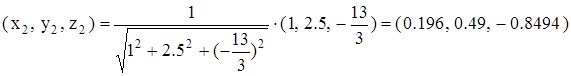