Изучение колебательных движений

ИССЛЕДОВАНИЕ НЕУПРУГОГО УДАРА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА

Цель работы: 1) пользуясь законами сохранения энергии и импульса определить скорость пули и работу деформации.

Оборудование: баллистический маятник, пружинный пистолет, пуля, шкала отсчета, линейка, секундомер.

Теоретическое введение

Баллистический маятник представляет собой цилиндр, заполненный пластилином, и подвешенный на четырех длинных нитях к потолку(Рисунок 1). Под цилиндром помещается шкала отсчета. Пружинный пистолет закрепляется специальным зажимом.

1. После выстрела пуля массой m и со скоростью υ застревает в пластилине и продолжает движение с цилиндром со скоростью u. На основании закона сохранения импульса имеем:

mυ = (m + M)u, (1)

где υ - скорость пули до удара, L

u - скорость пули с цилиндром

после удара, M - масса цилиндра. Н

При отклонении маятника в край-

нее положение, его кинетическая S

энергия переходит в потенциальную. Рисунок 1

(m + M)u²/2 = (m + M)gH, (2)

отсюда

u² = 2gH. (3)

Из рисунка 1 (при L >> H и малом угле α ) можно найти

H=S² / 2 L, (4)

где S – горизонтальное перемещение цилиндра вдоль шкалы,

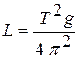. (5)

Решая совместно (1), (3), 4) и (5) найдем скорость пули:

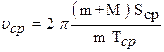. (6)

Относительная погрешность определения скорости рассчитывается по формуле

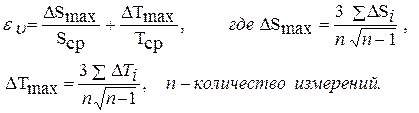(7)

Абсолютную погрешность 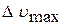определим:

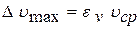. (8)

Считая удар пули о пластилин в цилиндре центральным неупругим ударом, а систему неизолированной, можно записать на основании закона сохранения энергии

mυ²/2 = (m + M)u²/2 + A, (9)

где A - энергия, затрачиваемая на деформацию тела, т.е. работа деформации. Решая совместно (1) и (8) найдем работу деформации

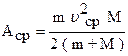, (10)

где υ - скорость пули, определяемая по формуле (6).

Абсолютную погрешность для работы деформации можно рассчитать по формуле

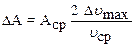. (11)

Порядок выполнения работы

1. Отметить на шкале положение стрелки при неподвижном цилиндре.

2. Зарядить пистолет.

3. Произвести выстрел и отметить положение стрелки при максималь­ном отбросе цилиндра. Одновременно с помощью секундомера заметить вре­мя 10 полных колебаний. Опыт произвести не менее 5 раз. Результаты за­нести в таблицу.

4. Из 10 полных колебаний определить период маятника T = t/10 для каждого опыта.

5. Подсчитав S_ср, Т_ср определить среднюю скорость пули υ_ср. по формуле (6) и работу деформации A_ср по формуле (10). Рассчитать погрешности определения этих величин по формулам (7), (8) и (11).

6. Окончательный результат записать в виде

υ = υ_ср ± Dυ_MAX, A= A_ср ± DA.

Таблица измерений

№ п/п	Si [м]	DS=|Si-Sср| [м]	ti (c)	Ti (c)	DT=|Ti-Tср| (c)	υср (м/c)	A (Дж)
1. 2. 3. 4. 5.
сумма
сред. знач.

Контрольные вопросы

1.Сформулируйте и запишите закон сохранения импульса и закон сохранения энергии.

2. Какая система называется изолированной ?

3. Что такое импульс тела, импульс силы ?

4. Напишите формулу механической работы.

5. Период колебаний математического маятника?

6. Виды деформаций. Закон Гука.

7. Закон изменения количества движения.

ЛАБОРАТОРНАЯ РАБОТА 14

ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНЫХ ДВИЖЕНИЙ

Цель работы: 1. Изучить характеристики колебаний физического маятника и определить его момент инерции.

2. Изучить характеристики колебаний пружинного маятника и определить коэффициент жесткости пружины.

Теоретические вопросы:Параметры гармонических колебаний: амплитуда, период, частота, фаза.Динамические и кинематические уравнения колебаний физического и математического маятников. Формулы периода колебаний физического и математического маятников.

Оборудование: установка с физическим и пружинным маятниками (штатив, пружина, груз, секундомер).

Теоретическое введение

Колебаниями называются процессы, характерной особенностью которых является повторяемость. Это могут быть качания маятников и сооружений, тепловые колебания ионов или молекул в узлах кристаллической решетки, и т.д. Колебания любой природы подчиняются общим законам. Простейшими колебаниями являются гармонические колебания, происходящие по законам синуса или косинуса.

X = Asin(wt + j_o), или X = Acos(wt + j_o), (1)

гдеX- смещение от положения равновесия; t- время колебательного процесса; A- максимальное смещение от положения равновесия или амплитуда ко­лебаний; wt+ j_o - фаза колебания; j_o - начальная фаза колебания.

За время равное периоду колебания (t=T) фаза изменяется на 2p. Периодом колебания Т называется длительность одного полного колебания. Величина n= 1/_Т показывающая, сколько раз в секунду повторяются колебания, называется частотой и измеряется в [Герцах]. Величина w = 2p/T показы­вающая, сколько раз за 2p секунд повторяется колебание, называется цик­лической частотой и измеряется в [^рад/_сек].

Причиной, вызывающей гармонические колебания, являются действия упругих или квазиупругих сил. Упругая сила определяется по закону Гука:

F= - kx, (2)

где к- коэффициент упругости (жесткости).

Второй закон Ньютона в этом случае имеет вид

F = ma = mdv/dt = md²x/dt² = - kх. (3)

Разделив обе части равенства на m получим выражение:

d²x/dt² = - kх/m.

Обозначим k/m =w², тогда d²x/dt² = - w²х или d²x/dt² + w²х = 0. Это есть динамическое уравнение колебаний пружинного маятника под действием упругих сил. Решением этого уравнения является уравнение:

X =Acoswt.

Т.к. w=2p/Т, то период колебания пружинного маятника выражается формулой:

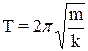. (4)

Отсюда коэффициент упругости (жесткости) пружинного маятника:

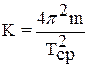. (5)

Изучим характеристики колебаний физического маятника. Физическим маятником является любое твердое тело, имеющее неподвижную ось враще­ния, если ось вращения не проходит через центр масс тела.

По второму закону Ньютона для вращающегося тела:

М= Je. (6)

Здесь J - статический момент инерции тела, e = d²j/dt² - угловое ускорение, М = Fr = - mgr = -mgLsinj -момент вращающей силы относительно оси вращения (скалярная величина числено равная произведению силы при­ложенной к телу на кратчайшее расстояние между осью вращения тела и вектором приложенной силы, считается, если тело вращается против часовой стрелки относительно оси вращения, то момент вращающей силы берется со знаком минус).

Тогда J(d²j/dt²) = - mgLsinj, разделив обе части выражения на J и предположив, что sinj = j для малых углов, получим выражение динамического уравнения колебаний физического маятника:

d² j/dt²+(mgLj)/J= 0,

обозначив (mgL)/J= w² имеем

d² j/dt²+w²j=0. (7)

Решением этого уравнения является функция:

j= j_ocos(wt+a₀). (8)

Период колебания физического маятника вычисляется по формуле:

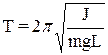. (9)

Отсюда статический момент инерции физического маятника, вращающегося относительно неподвижной оси вычисляется по формуле:

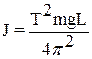. (10)

Порядок выполнения работы

Задание 1.

1. На штативе укрепить пружину и подвесить к ней груз известной массой.(m = 1кг, ∆ m = 0,001кг)

2. Оттянув груз, возбудить малые колебания. С помощью секундомера определить время десяти полных колебаний и записать в таблицу. Измерения повторить не менее трех раз. Найти среднее значение времени.

3. Подсчитать период колебания: Т= t/N, где N- число колебаний.

4. По формуле 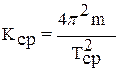определить коэффициент жесткости пружины.

5. Определить абсолютную погрешность измерений Dt, DT,

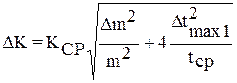, где .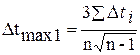

6. Определить относительную погрешность косвенного измерения коэффициента жесткости пружины по формуле:

e_к=(DK/K_ср) ^. 100 %.

7. Запишите результаты измерений в виде: m = (m ± Dm), t = (t_ср ± Dt_мах), K=(K_ср ± DK_мах), e_к.

Таблица измерений

№ п/п	ti (c)	Dti =êti - tср êс	Ti (c)	DTi =|Ti- Tcp |(c)	K (Н/м)
1. 2. 3. 4. 5.
Сумма
Среднее значение

Задание 2.

1. Физический маятник (стержень) установить на опоре и вывести его из положения равновесия.

2. Измерить время 10 полных колебаний и записать в таблицу. Изме­рения производить не менее 5-ти раз, найти среднее значение.

3. Рассчитать значение периода Т=t/N, абсолютную погрешность DТ. N - количество колебаний

4. Измерить расстояние от точки подвеса до центра масс.

L = (0,42 ± 0,002) [м].

5. По формуле 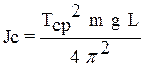подсчитать момент инерции стержня.

6. Подсчитать абсолютную погрешность измерения момента инерции.

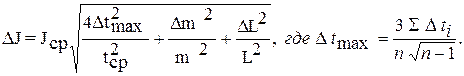
7. Определить относительную погрешность измерения момента инерции

e_J = (DJ/J_ср) ^. 100 %.

8. Записать результат измерений в виде: e _J [%], J =(J_ср ± DJ).

Таблица измерений

№ п/п	ti (с)	Dti(с)	Тi(c)	DТi(c)	J (кг . м2)
Сумма
Ср.зн.

Контрольные вопросы

1. Основные виды колебаний.

2. Уравнение гармонических колебаний. Скорость и ускорение гармонических колебаний.

3. Сложение гармонических колебаний.

4. Энергия гармонических колебаний.

5. Затухающие и вынужденные колебания. Резонанс.