Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор формы уравнения множественной регрессии
Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Спецификация модели включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Требования к факторам:1 Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов) 2.Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда Ryx1 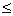 Rx1x2 для зависимости y=a+b1x1+b2+...+bpxp+e может привести к нежелательным последствиям, повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретированными. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной.
Rx1x2 для зависимости y=a+b1x1+b2+...+bpxp+e может привести к нежелательным последствиям, повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретированными. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной.
Выбор формы уравнения
• 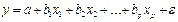 Линейная регрессия
Линейная регрессия
• Линеаризуемые регрессии
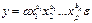 - Степенная регрессия
- Степенная регрессия
- Экспоненциальная регрессия
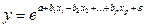 |
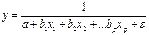 - Гиперболическая регрессия
- Гиперболическая регрессия
Параметры каждого из перечисленных выше уравнений (трендов) можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой переменной - фактические уровни временного ряда yt. Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни уt и уt-1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации R2 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации.
