Краткие теоретические сведения. Расстояние между двумя точками А1(х1; у1) и А2(х2; у2) находится по формуле
Расстояние между двумя точками А1(х1; у1) и А2(х2; у2) находится по формуле
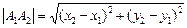 . (1)
. (1)
Уравнение прямой А1А2, проходящей через точки А1(х1; у1) и А2(х2; у2), имеет вид
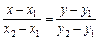 . (2)
. (2)
Уравнение прямой, проходящей через точку М0(x0; y0) и имеющей угловой коэффициент k, записывается в следующем виде:
y – y0 = k · (x – x0). (3)
Общее уравнение прямой имеет вид
Ax + By + C = 0. (4)
Вектор 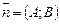 называется нормальным вектором.
называется нормальным вектором.
Координаты точки (x0; y0), являющейся серединой отрезка А1А2 с концами в указанных точках, вычисляются по формулам
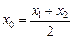 ,
, 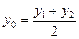 . (5)
. (5)
Тангенс угла 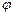 между прямыми y1 = k1x + b1, y2 = k2x + b2 определяется следующей формулой:
между прямыми y1 = k1x + b1, y2 = k2x + b2 определяется следующей формулой:
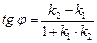 . (6)
. (6)
Следствие 1.Две прямые y1 = k1x + b1, y2 = k2x + b2 параллельны тогда и только тогда, когда
k1 = k2. (7)
Следствие 2.Две прямые y1 = k1x + b1, y2 = k2x + b2 взаимно перпендикулярны тогда и только тогда, когда
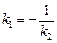 . (8)
. (8)
Расстояние d от точки М0(x0; y0) до прямой (4) вычисляется по формуле
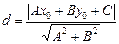 . (9)
. (9)
Уравнение окружности радиуса R с центром в точке М0 (x0; y0) имеет вид
(x – x0)2 + (y – y0)2 = R2. (10)
Каноническое уравнение эллипса (рис. 1) записывается в виде
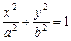 . (11)
. (11)
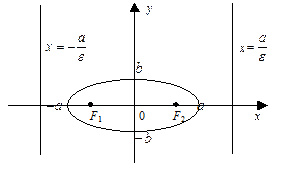 |
| Рис. 1 |
На рис. 1 F1(–c; 0), F2(c; 0) — фокусы, c = 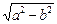 , а — большая полуось, b — малая полуось,
, а — большая полуось, b — малая полуось, 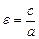 — эксцентриситет (
— эксцентриситет ( 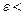 1, так как
1, так как  ), x =
), x = 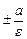 — директрисы.
— директрисы.
Каноническое уравнение гиперболы (рис. 2) имеет вид 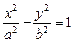 . (12) На рис. 2 F1(–c; 0), F2(c; 0) — фокусы, c = . (12) На рис. 2 F1(–c; 0), F2(c; 0) — фокусы, c = 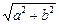 , а — действительная полуось, b — мнимая полуось, , а — действительная полуось, b — мнимая полуось, 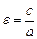 — эксцентриситет ( — эксцентриситет ( 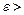 1, так как 1, так как 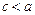 ), ), 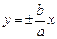 — асимптоты, — асимптоты, 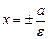 — директрисы. — директрисы. | |
 | |
| Рис. 2 | |
Каноническое уравнение параболы (рис. 3) имеет вид
y2 = 2px. (13)
При этом 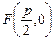 — фокус,
— фокус, 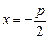 — директриса (р — параметр параболы, расстояние от фокуса параболы до ее директрисы).
— директриса (р — параметр параболы, расстояние от фокуса параболы до ее директрисы).
 |
| Рис. 3 |
Другие случаи расположения параболы указаны на рисунках 4–6.
Точки, симметричные относительно прямой, — это точки, лежащие на одном перпендикуляре к прямой, на одинаковых расстояниях и по разные стороны от нее.
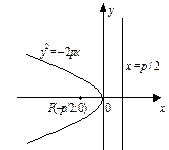 | 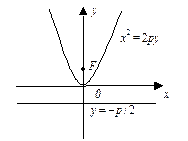 |
| Рис. 4 | Рис. 5 |
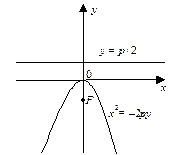 | |
| Рис. 6 | |
Вопросы для самопроверки
1. Как в аналитической геометрии определяется линия? Приведите примеры.
2. Каким образом находится точка пересечения двух линий на плоскости? Приведите примеры.
3. Какие существуют методы построения прямой на плоскости? Какие виды уравнений прямой на плоскости вы знаете?
4. Как находится длина высоты в треугольнике? Приведите примеры.
5. Какие условия являются необходимыми и достаточными для параллельности и перпендикулярности двух прямых?
6. Какая точка называется образом точки М при осевой симметрии?
7. Какие существуют типы кривых второго порядка? Каковы канонические уравнения окружности, эллипса, гиперболы, параболы?
8. Что мы называем фокусами и эксцентриситетом эллипса, гиперболы? Что называется фокусом, директрисой параболы? Что мы называем асимптотами гиперболы?
9. Как определить координаты начала новой системы координат относительно старой при параллельном переносе?
10. Какие примеры зависимостей между величинами в экономике, которые выражаются алгебраическими уравнениями первого и второго порядков, вы знаете?
Типовая задача 1
Даны вершины А(–1; 1), В(5; 4), С(2; 5) треугольника АВС.
Найти: 1) длину стороны АВ; 2) внутренний угол А; 3) уравнение медианы, проведенной из вершины С; 4) точку Р пересечения высот треугольника; 5) длину высоты, опущенной из вершины С; 6) образ точки Р при осевой симметрии относительно прямой АВ; 7) уравнение прямой а, проходящей через точку Р, параллельной прямой АВ. Сделать чертеж.
Решение. На рис. 7 представим чертеж.
 |
| Рис. 7 |
1)По формуле (1) имеем:
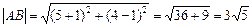 .
.
2) Определим вначале по формуле (2) уравнения прямых АВ, АС и их угловые коэффициенты.
Уравнение прямой АВ:
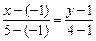 .
.
Отсюда 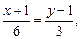
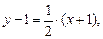
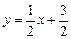

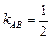 .
.
Уравнение прямой АС:
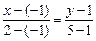 .
.
Отсюда 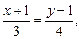
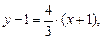
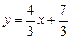

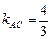 .
.
По формуле (6) находим тангенс угла между прямыми АВ и АС:
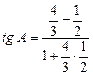
 tg A =
tg A = 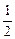

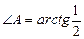 .
.
3) По формулам (5) находим координаты середины М стороны АВ треугольника:
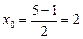 ,
, 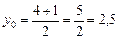 , М (2; 2,5).
, М (2; 2,5).
По формуле (2) находим уравнение медианы СМ:
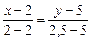 ,
, 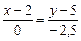 .
.
Раскрывая пропорцию, имеем x – 2 = 0  x = 2.
x = 2.
Это и есть искомое уравнение медианы.
4) По формуле (2) определим уравнение третьей прямой ВС треугольника:
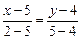 ,
, 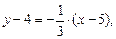
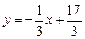 .
.
Отсюда 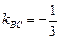 .
.
Пусть 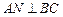 , тогда по формуле (8) имеем:
, тогда по формуле (8) имеем: 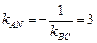 .
.
Используя формулу (3), запишем уравнение прямой АN:
y – 1 = 3 · (x –(–1))  y = 3x + 4.
y = 3x + 4.
Аналогично находим уравнение прямой ВК, которая перпендикулярна АС. Так как 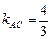 ,
, 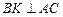 , то по следствию 2 имеем:
, то по следствию 2 имеем:
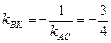 ;
; 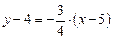 ,
,
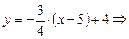
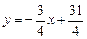 .
.
Координаты точки Р находим как решение системы уравнений, составленной из уравнений высот АN и ВК:
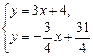

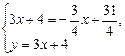

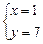 , т. е. Р(1; 7).
, т. е. Р(1; 7).
5) Длина высоты СЕ, опущенной из вершины С на сторону АВ, есть расстояние от этой точки С до АВ. Найдем уравнение прямой АВ:
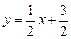
 x – 2y + 3 = 0.
x – 2y + 3 = 0.
По формуле (9), 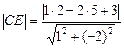 =
= 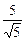 =
= 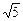 .
.
6) Пусть 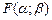 — образ точки Р(1; 7) при осевой симметрии
— образ точки Р(1; 7) при осевой симметрии
с осью симметрии АВ. Тогда на основании определения осевой
симметрии 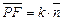 (
( 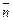 — нормальный вектор прямой АВ) и
— нормальный вектор прямой АВ) и 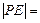
= 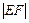 . Так как
. Так как 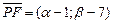 ,
, 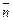 =(1; –2), то
=(1; –2), то 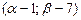 =
= 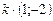 .
.
Отсюда 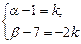

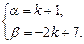
Из формулы (9) получим:
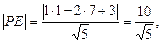
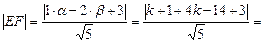
= 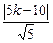 .
.
Так как 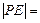
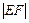 , то
, то 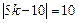
 5k – 10 =
5k – 10 = 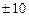

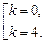
При k = 0 получаем известную точку P(1; 7), при k = 4 — точку F(5; –1).
7) По формуле (7), так как 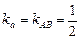 и P(1; 7), имеем:
и P(1; 7), имеем: 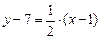 . Следовательно,
. Следовательно, 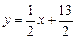 — уравнение прямой а.
— уравнение прямой а.
Ответ: 1) 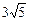 ; 2)
; 2) 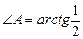 ;3) х = 2; 4) Р(1; 7);5)
;3) х = 2; 4) Р(1; 7);5) 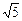 ;
;
6) F(5; –1); 7) 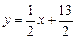 .
.
Во втором задании необходимо составить уравнение линии, обладающей определенным свойством.
Алгоритм решения задачи этого задания может быть следующим:
1. Выбирается произвольная точка М(х; у) данной линии.
2. В координатной форме составляется уравнение линии на основе учета ее указанных свойств.
3. С помощью алгебраических преобразований полученное уравнение приводится к каноническому виду.
Типовая задача 2
Составить уравнение линии, если отношение расстояний от каждой ее точки до точки А(–1; 0) и до прямой х = –4 равно 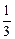 . Построить график.
. Построить график.
Решение. 1. Пусть М(х; у) — произвольная точка данной линии.
2. По формуле (1) находим расстояние 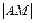 и расстояние от точки М до ее проекции М1на прямую х = –4:
и расстояние от точки М до ее проекции М1на прямую х = –4:
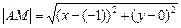 =
= 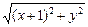 ,
,
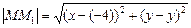 =
= 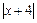 .
.
По условию задачи,  .
.
3. Преобразуем полученное уравнение:
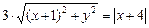
 9 · (x2 + 2x + 1 + y2) = x2 + 8x + 16.
9 · (x2 + 2x + 1 + y2) = x2 + 8x + 16.
Отсюда 8х2 + 10х + 9у2 +(–7) = 0 
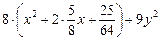 =
=
= 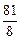

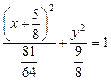 .
.
С помощью формул параллельного переноса приведем уравнение к каноническому виду.
Пусть 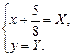 (14)
(14)
Тогда  уравнение линии запишем в виде
уравнение линии запишем в виде 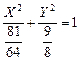 . Это уравнение эллипса с полуосями
. Это уравнение эллипса с полуосями 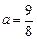 и
и 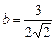 . Так как
. Так как 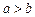 , то фокусы его находятся на оси ОХ. Из формул (14) получаем
, то фокусы его находятся на оси ОХ. Из формул (14) получаем 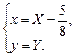
Точка О¢ 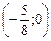 есть начало новой системы координат ХОY относительно старой. Строим график данного эллипса в новой системе координат (рис. 8).
есть начало новой системы координат ХОY относительно старой. Строим график данного эллипса в новой системе координат (рис. 8).
Ответ: 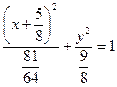 . . | 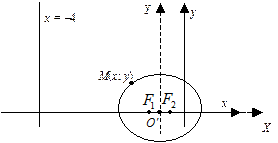 |
| Рис. 8 |
2. Задания 3 и 4
по теме
«Элементы линейной алгебры и теории
n-мерных векторных пространств»
