Самостоятельная работа обучающегося с преподавателем 2 страница
В предыдущих параграфах были введены два единичных ортогональных вектора: вектор 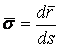 , направленный по касательной к кривой, и вектор главной нормали , направленный по касательной к кривой, и вектор главной нормали 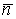 , который определён первой формулой Френе (1.9). Введём единичный вектор , который определён первой формулой Френе (1.9). Введём единичный вектор 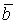 , ортогональный векторам , ортогональный векторам 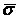 и и 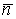 , как векторное произведение , как векторное произведение 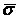 на на 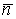 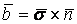 . (2.1) Нормаль, которая определяется вектором . (2.1) Нормаль, которая определяется вектором 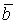 , называется Бинормалью. Очевидно, что получена правая тройка ортогональных векторов. Этот подвижный базис (или репер), который сопровождает точку М при её движении по кривой, называется Подвижным, а также Естественным базисом или Репером Френе (Френе – французский геометр XIX века, который в 1847 году первым написал формулы для производных по длине дуги трёх базисных векторов , называется Бинормалью. Очевидно, что получена правая тройка ортогональных векторов. Этот подвижный базис (или репер), который сопровождает точку М при её движении по кривой, называется Подвижным, а также Естественным базисом или Репером Френе (Френе – французский геометр XIX века, который в 1847 году первым написал формулы для производных по длине дуги трёх базисных векторов 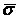 , , 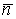 , , 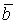 ). Плоскость, проходящая через вектора ). Плоскость, проходящая через вектора 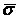 и и 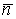 , называется Соприкасающейся, через вектора , называется Соприкасающейся, через вектора 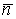 и и 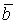 – Нормальной, а через вектора – Нормальной, а через вектора 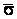 и и 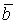 – Спрямляющей. Эти три плоскости образуют так называемый Естественный трехгранник, или Трехгранник Френе (рис. 2.1). – Спрямляющей. Эти три плоскости образуют так называемый Естественный трехгранник, или Трехгранник Френе (рис. 2.1). 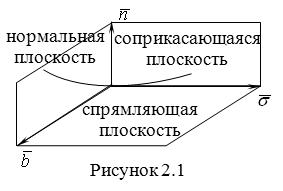 Уравнение (1.9) определяет производную Уравнение (1.9) определяет производную 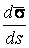 . Для того, чтобы получить производные от векторов . Для того, чтобы получить производные от векторов 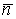 и и 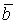 , обратимся к формуле (2.1). Дифференцируя по , обратимся к формуле (2.1). Дифференцируя по 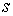 и используя формулу (1.9), имеем и используя формулу (1.9), имеем 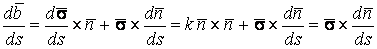 . Отсюда следует, что вектора . Отсюда следует, что вектора 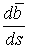 и и 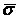 ортогональны. Кроме того, ортогональны. Кроме того, 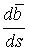 ортогонально ортогонально 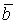 (см п.3о в 1.2). Таким образом, направление вектора (см п.3о в 1.2). Таким образом, направление вектора 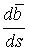 совпадает с направлением вектора главной нормали совпадает с направлением вектора главной нормали 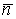 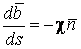 . (2.2) Это Вторая формула Френе, где коэффициент . (2.2) Это Вторая формула Френе, где коэффициент 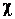 характеризует степень изменяемости вектора характеризует степень изменяемости вектора 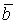 по длине дуги, то есть поворот соприкасающейся плоскости. Если по длине дуги, то есть поворот соприкасающейся плоскости. Если 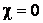 , то кривая лежит в этой плоскости. Коэффициент , то кривая лежит в этой плоскости. Коэффициент 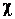 называется кручением. Теперь рассмотрим называется кручением. Теперь рассмотрим 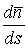 . Этот вектор ортогонален . Этот вектор ортогонален 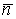 (по формуле (1.4)), поэтому в разложении по ортогональному базису (по формуле (1.4)), поэтому в разложении по ортогональному базису 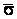 , , 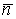 , , 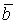 , , 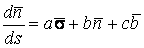 , (2.3) Коэффициент , (2.3) Коэффициент 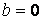 . Продифференцируем равенство . Продифференцируем равенство 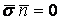 : : 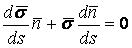 . В последнее соотношение подставим выражение . В последнее соотношение подставим выражение 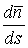 из (2.3) и из (2.3) и 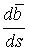 из (1.9). Получаем равенство из (1.9). Получаем равенство 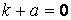 , отсюда коэффициент , отсюда коэффициент 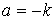 . Поскольку . Поскольку 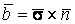 , получаем , получаем 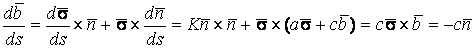 . (2.4) С другой стороны, по второй формуле Френе . (2.4) С другой стороны, по второй формуле Френе 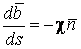 . Таким образом, С= . Таким образом, С= 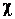 , и , и 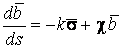 . (2.5) Это Третья формула Френе. По определению кривизна . (2.5) Это Третья формула Френе. По определению кривизна 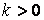 , но кручение , но кручение 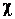 может быть любого знака. Для вычисления кручения используем вторую формулу Френе может быть любого знака. Для вычисления кручения используем вторую формулу Френе 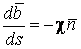 . Умножив скалярно на . Умножив скалярно на 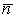 левую и правую части равенства, получим левую и правую части равенства, получим 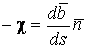 . С учётом равенства . С учётом равенства 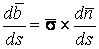 (см. формулу (2.4)), имеем (см. формулу (2.4)), имеем 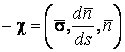 , Где в круглых скобках записано смешанное произведение трёх векторов. Поскольку , Где в круглых скобках записано смешанное произведение трёх векторов. Поскольку 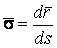 , а из первой формулы Френе следует, что , а из первой формулы Френе следует, что 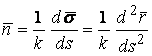 , то , то  , (2.6) Где в данном случае штрих означает дифференцирование по , (2.6) Где в данном случае штрих означает дифференцирование по 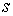 . . | |||
| 2.2 Анализ системы уравнений Френе |  |  |  |
Система уравнений Френе (1.9), (2.2) и (`2.5) характеризует перемещение трёхгранника Френе, который определяется векторами 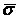 , , 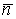 , , 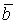 вдоль заданной кривой. При описании некоторых физических процессов, например, в гидроаэромеханике, вместо неподвижной координатной системы с успехом используют Подвижный (естественный) базис, составленный из указанных векторов, который перемещается вдоль траектории движения вместе с некоторой заданной точкой материальной среды. Систему уравнений Френе разобьём на две подсистемы, первая из которых записывается при вдоль заданной кривой. При описании некоторых физических процессов, например, в гидроаэромеханике, вместо неподвижной координатной системы с успехом используют Подвижный (естественный) базис, составленный из указанных векторов, который перемещается вдоль траектории движения вместе с некоторой заданной точкой материальной среды. Систему уравнений Френе разобьём на две подсистемы, первая из которых записывается при 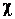 =0, а вторая при =0, а вторая при 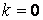  , , 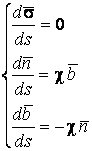 . (2.7) В первой подсистеме вектор бинормали . (2.7) В первой подсистеме вектор бинормали 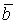 является постоянным и определяет ось вращения трёхгранника Френе при движении вдоль кривой; во второй подсистеме ось вращения – касательная, которая определяется фиксированным вектором является постоянным и определяет ось вращения трёхгранника Френе при движении вдоль кривой; во второй подсистеме ось вращения – касательная, которая определяется фиксированным вектором 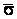 . Таким образом, в первом случае получаем движение в соприкасающейся плоскости, причем скорость вращения определяется коэффициентом . Таким образом, в первом случае получаем движение в соприкасающейся плоскости, причем скорость вращения определяется коэффициентом 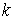 , а во втором – в нормальной плоскости, при этом скорость вращения определяется коэффициентом , а во втором – в нормальной плоскости, при этом скорость вращения определяется коэффициентом 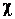 . В силу линейности уравнений полную систему уравнений получаем сложением двух подсистем (2.7). Соответственно полная скорость вращения состоит из двух компонент . В силу линейности уравнений полную систему уравнений получаем сложением двух подсистем (2.7). Соответственно полная скорость вращения состоит из двух компонент 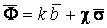 . Отметим также, что система уравнений Френе может быть в некоторых случаях проинтегрирована, среди этих случаев выделим простейшие: 1) . Отметим также, что система уравнений Френе может быть в некоторых случаях проинтегрирована, среди этих случаев выделим простейшие: 1) 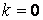 ,тогда ,тогда 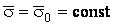 . Поскольку . Поскольку 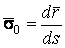 , то , то 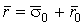 . Вводя координаты векторов . Вводя координаты векторов 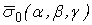 , , 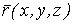 , , 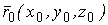 , получаем, исключая параметр , получаем, исключая параметр 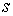 , известные уравнения прямой линии , известные уравнения прямой линии 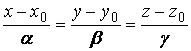 . 2) . 2) 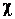 =0, тогда =0, тогда 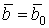 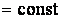 , при этом получаем плоскую кривую. 3) Винтовая линия (см. пример в разделе 1.6). Было показано, что кривизна K , при этом получаем плоскую кривую. 3) Винтовая линия (см. пример в разделе 1.6). Было показано, что кривизна K 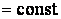 Вычисления показывают, что и кручение Вычисления показывают, что и кручение 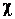 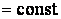 Оказывается, что это единственная линия, у которых кручение пропорционально кривизне Оказывается, что это единственная линия, у которых кручение пропорционально кривизне 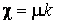 . В общем случае три уравнения Френе связывают девять скалярных компонент трёх векторов . В общем случае три уравнения Френе связывают девять скалярных компонент трёх векторов 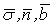 . Однако существуют ещё шесть условий, наложенные на эти компоненты. Это условия ортогональности векторов, а также условия, вытекающие из того факта, что эти вектора единичные . Однако существуют ещё шесть условий, наложенные на эти компоненты. Это условия ортогональности векторов, а также условия, вытекающие из того факта, что эти вектора единичные 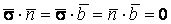 , , 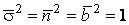 . (2.8) Общее число уравнений ((1.9), (2.2),(2.5) и (2.8)) равно девяти, что совпадает с числом скалярных компонент векторов . (2.8) Общее число уравнений ((1.9), (2.2),(2.5) и (2.8)) равно девяти, что совпадает с числом скалярных компонент векторов 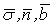 . Кроме того, в уравнения Френе входят кривизна . Кроме того, в уравнения Френе входят кривизна 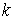 и кручение и кручение 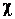 . Теорема о существовании и единственности решения системы уравнений Френе, дополненной соотношениями (2.8), формулируется здесь без доказательства. Теорема. Если заданы кривизна и кручение как непрерывные функции длины дуги . Теорема о существовании и единственности решения системы уравнений Френе, дополненной соотношениями (2.8), формулируется здесь без доказательства. Теорема. Если заданы кривизна и кручение как непрерывные функции длины дуги 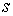 , то существует единственное решение системы уравнений Френе (1.9), (2.2), (2.5) , то существует единственное решение системы уравнений Френе (1.9), (2.2), (2.5) 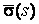 , , 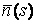 и и 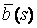 , удовлетворяющее соотношениям (2.8) и следующим начальным условиям: в данной точке , удовлетворяющее соотношениям (2.8) и следующим начальным условиям: в данной точке 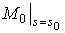 задан естественный трёхгранник Френе задан естественный трёхгранник Френе 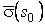 , , 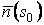 и и 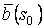 . Это решение определено в некоторой окрестности точки . Это решение определено в некоторой окрестности точки 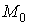 . В свою очередь, полученный естественный трёхгранник Френе однозначно определяет пространственную кривую, а именно, текущий радиус-вектор . В свою очередь, полученный естественный трёхгранник Френе однозначно определяет пространственную кривую, а именно, текущий радиус-вектор 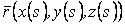 . . | ||||
| 3.1. Поверхность в пространстве. Касательная плоскость и нормаль к поверхности в пространстве |  |  |  | |
Известно, что поверхность в пространстве определяется уравнением 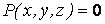 , (3.1) Связывающем прямоугольные декартовые координаты , (3.1) Связывающем прямоугольные декартовые координаты 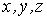 . Другой способ аналитического описания поверхности – использование парaметрических уравнений . Другой способ аналитического описания поверхности – использование парaметрических уравнений 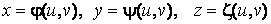 . (3.2) Исключая параметры . (3.2) Исключая параметры 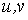 , мы возвращаемся к уравнению (3.1), связывающему переменные , мы возвращаемся к уравнению (3.1), связывающему переменные 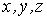 . Пусть задана некоторая точка . Пусть задана некоторая точка 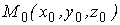 на поверхности. Возьмём произвольную кривую, лежащую на поверхности и проходящую через эту точку. Пусть кривая определяется уравнениями на поверхности. Возьмём произвольную кривую, лежащую на поверхности и проходящую через эту точку. Пусть кривая определяется уравнениями 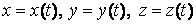 . Подставляя эти соотношения в (3.1) и дифференцируя по параметру . Подставляя эти соотношения в (3.1) и дифференцируя по параметру 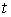 , получаем , получаем 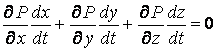 . (3.3) Равенство (3.3) можно рассматривать как условие ортогональности вектора . (3.3) Равенство (3.3) можно рассматривать как условие ортогональности вектора 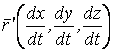 , направленного по касательной к кривой, а значит, и к поверхности, и вектора , направленного по касательной к кривой, а значит, и к поверхности, и вектора 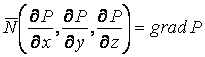 . Поскольку кривая выбрана произвольно, то вектор . Поскольку кривая выбрана произвольно, то вектор 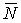 ортогонален ко всем касательным к поверхности, проходящим через точку ортогонален ко всем касательным к поверхности, проходящим через точку 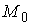 (эти касательные заполняют касательную плоскость). Вектор (эти касательные заполняют касательную плоскость). Вектор 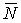 называется нормальным вектором плоскости. Уравнения касательной плоскости и нормали к поверхности в точке называется нормальным вектором плоскости. Уравнения касательной плоскости и нормали к поверхности в точке 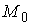 имеют вид имеют вид 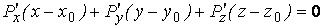 , , 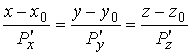 , (3.4) Где все производные вычисляются в точке , (3.4) Где все производные вычисляются в точке 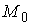 . Заметим, что всё здесь сказанное о касательной плоскости и нормали относится к неособым точкам поверхности. Особые точки поверхности, для которых выписанные формулы не имеют смысла, определяются равенствами . Заметим, что всё здесь сказанное о касательной плоскости и нормали относится к неособым точкам поверхности. Особые точки поверхности, для которых выписанные формулы не имеют смысла, определяются равенствами 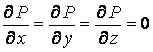 . Теперь обратимся к параметрическим уравнениям поверхности. Подставляя соотношения (3.2) в уравнения (3.1) и дифференцируя по . Теперь обратимся к параметрическим уравнениям поверхности. Подставляя соотношения (3.2) в уравнения (3.1) и дифференцируя по 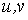 , имеем , имеем 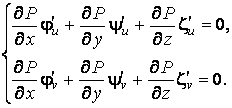 Отсюда получаем, что Отсюда получаем, что 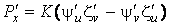 , , 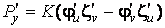 , , 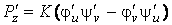 , Где К – некоторая постоянная. Последние равенства дают возможность записать уравнения касательной плоскости и нормали к поверхности, представленные формулами (3.4), в параметрическом виде. Параметры , Где К – некоторая постоянная. Последние равенства дают возможность записать уравнения касательной плоскости и нормали к поверхности, представленные формулами (3.4), в параметрическом виде. Параметры 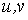 определяют положение точки на поверхности, поэтому их называют криволинейными координатами на поверхности. Координатные линии определяют положение точки на поверхности, поэтому их называют криволинейными координатами на поверхности. Координатные линии 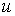 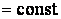 или или 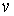 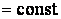 в общем случае будут кривыми линиями. Линия в общем случае будут кривыми линиями. Линия 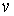 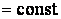 , вдоль которой изменяется только параметр , вдоль которой изменяется только параметр 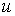 , называется линией , называется линией 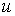 , а линия , а линия 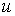 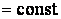 , вдоль которой изменяется только параметр , вдоль которой изменяется только параметр 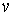 – линией – линией 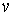 | ||||
| 3.2. Первая квадратичная форма поверхности. Дифференциальный элемент площади поверхности |  |  |  | |
Рассмотрим квадрат дифференциала длины дуги любой линии на поверхности 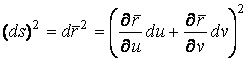 . Подставляя в это последнее равенство выражения . Подставляя в это последнее равенство выражения 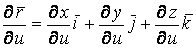 и и 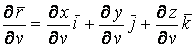 и выделяя коэффициенты при и выделяя коэффициенты при 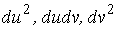 , получаем , получаем  , (3.5) Где , (3.5) Где 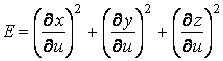 , , 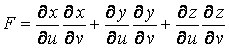 , , 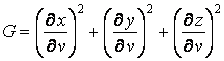 . (3.6) Как видно из последних формул, коэффициенты . (3.6) Как видно из последних формул, коэффициенты 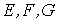 не зависят от выбора линии на поверхности, а зависят только от вида поверхности и от координат точки. Квадратичная форма не зависят от выбора линии на поверхности, а зависят только от вида поверхности и от координат точки. Квадратичная форма 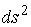 , определённая в (3.5), называется Первой квадратичной формой поверхности (или Первой дифференциальной формой Гаусса, а также Линейным элементом поверхности). Это основная метрическая форма поверхности. Она инвариантна в том смысле, что не меняется при перемещении поверхности как твёрдого тела, и не зависит от преобразования декартовой системы координат. Если обозначить , определённая в (3.5), называется Первой квадратичной формой поверхности (или Первой дифференциальной формой Гаусса, а также Линейным элементом поверхности). Это основная метрическая форма поверхности. Она инвариантна в том смысле, что не меняется при перемещении поверхности как твёрдого тела, и не зависит от преобразования декартовой системы координат. Если обозначить 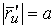 , , 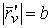 , То из (3.6) следует, что , То из (3.6) следует, что 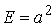 , , 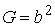 , , 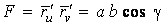 , Где G – угол между векторами , Где G – угол между векторами 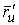 и и 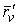 , то есть угол, под которым пересекаются координатные линии. Кроме того, , то есть угол, под которым пересекаются координатные линии. Кроме того, 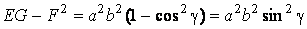 . (3.7) Следовательно, коэффициенты . (3.7) Следовательно, коэффициенты 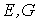 и дискриминант и дискриминант 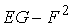 – положительны, а квадратичная форма – положительны, а квадратичная форма 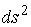 положительно определена. Коэффициент положительно определена. Коэффициент 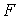 может быть и положительным, и отрицательным в зависимости от знака может быть и положительным, и отрицательным в зависимости от знака 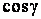 , то есть в зависимости от того, будет ли координатный угол острым или тупым. Если , то есть в зависимости от того, будет ли координатный угол острым или тупым. Если 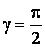 , то координатные линии ортогональны и , то координатные линии ортогональны и 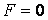 . Заметим также, что . Заметим также, что 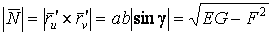 . (3.8) . (3.8) | |||
| 3.3. Угол пересечения двух линий на поверхности |  |  |  |
Рассмотрим две линии на поверхности в точке 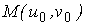 . Параметры, относящиеся к этим двум линиям, обозначим соответственно . Параметры, относящиеся к этим двум линиям, обозначим соответственно 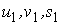 и и 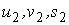 . Тогда единичные вектора касательных к этим линиям в общей точке М будут . Тогда единичные вектора касательных к этим линиям в общей точке М будут  и и  . Под углом J между линиями в точке пересечения М будем понимать угол между векторами касательных к этим линиям. Вычислим . Под углом J между линиями в точке пересечения М будем понимать угол между векторами касательных к этим линиям. Вычислим 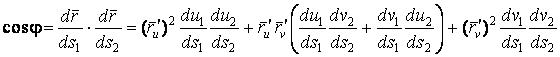 . Используя обозначения предыдущего параграфа, запишем . Используя обозначения предыдущего параграфа, запишем  . (3.9) Условие ортогональности линий – это . (3.9) Условие ортогональности линий – это 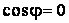 , или , или  . (3.10) . (3.10) | |||
| 3.4. Дифференциал площади поверхности |  |  |  |
Рассмотрим координатную сеть линий на поверхности и криволинейный четырёхугольник, образованный линиями с постоянными значениями координат U И U+DU, V И V+DV, пересекающимися в точках 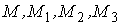 (рис. 3.1). Выделяя главные части приращений (рис. 3.1). Выделяя главные части приращений 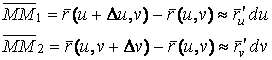 И приближенно (при малых И приближенно (при малых 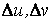 ) заменяя криволинейный четырёхугольник параллелограммом, построенным на векторах ) заменяя криволинейный четырёхугольник параллелограммом, построенным на векторах 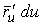 и и 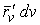 , как показано на рис. 2.1, запишем площадь параллелограмма в виде , как показано на рис. 2.1, запишем площадь параллелограмма в виде 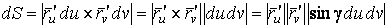 . С учётом формулы (3.7) находим . С учётом формулы (3.7) находим 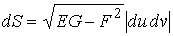 . (3.11) . (3.11) 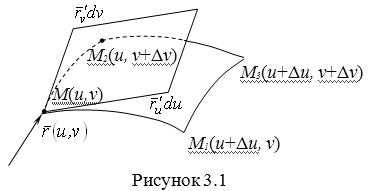 Поскольку криволинейный четырёхугольник мало отличается от параллелограмма при Поскольку криволинейный четырёхугольник мало отличается от параллелограмма при 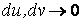 , величину , величину 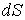 называют Дифференциалом площади поверхности Пример 1. Геликоид. Эта поверхность получается при винтовом движении отрезка прямой, параллельного плоскости называют Дифференциалом площади поверхности Пример 1. Геликоид. Эта поверхность получается при винтовом движении отрезка прямой, параллельного плоскости 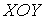 и пересекающего ось и пересекающего ось 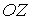 (ось винтового движения). Проекция отрезка прямой на плоскость (ось винтового движения). Проекция отрезка прямой на плоскость 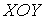 равномерно вращается около начала координат, а точка пересечения с осью равномерно вращается около начала координат, а точка пересечения с осью 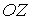 равномерно перемещается по этой оси (рис. 3.2). Запишем вектора равномерно перемещается по этой оси (рис. 3.2). Запишем вектора 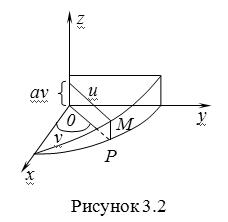 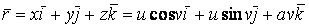 , , 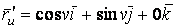 , , 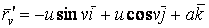 , ,  Тогда Тогда 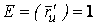 , , 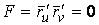 , , 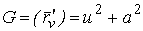 , линейный элемент , линейный элемент 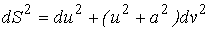 . Координатные линии здесь записываются таким образом: – линия . Координатные линии здесь записываются таким образом: – линия 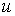 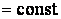 – винтовая линия; при полном обороте (на угол 2P) проекции – винтовая линия; при полном обороте (на угол 2P) проекции 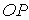 точка М поднимается на 2PА, где А – шаг винта; – линия точка М поднимается на 2PА, где А – шаг винта; – линия 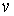 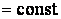 во всех точках имеет одну и ту же аппликату во всех точках имеет одну и ту же аппликату 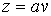 ; проекция линии на плоскость ; проекция линии на плоскость 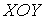 Определяется уравнением Определяется уравнением 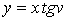 . . 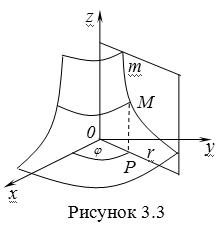 Пример 2. Поверхность вращения. Пусть в плоскости, проходящей через ось Oz , задана линия M Пример 2. Поверхность вращения. Пусть в плоскости, проходящей через ось Oz , задана линия M 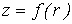 , Где Z И R - прямоугольные декартовы координаты в этой плоскости, причем ось Or лежит на пересечении этой плоскости с плоскостью XOY. Пусть теперь M вращается вокруг оси Oz. Вводя на плоскости XOY полярные координаты R,J, получаем для точки P (проекции точки M, лежащей на линии M) следующие координаты, которые при вращении линии будут изменяться вместе с углом вращения j , Где Z И R - прямоугольные декартовы координаты в этой плоскости, причем ось Or лежит на пересечении этой плоскости с плоскостью XOY. Пусть теперь M вращается вокруг оси Oz. Вводя на плоскости XOY полярные координаты R,J, получаем для точки P (проекции точки M, лежащей на линии M) следующие координаты, которые при вращении линии будут изменяться вместе с углом вращения j 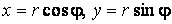 . Точка М имеет эти две координаты и ещё третью координату . Точка М имеет эти две координаты и ещё третью координату 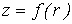 . Таким образом, радиус-вектор произвольной точки, лежащей на поверхности вращения, имеет вид . Таким образом, радиус-вектор произвольной точки, лежащей на поверхности вращения, имеет вид 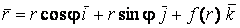 , , 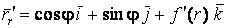 , , 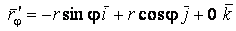 , , 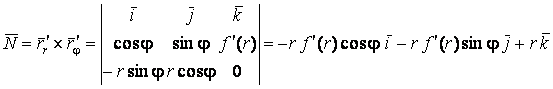 . Тогда . Тогда 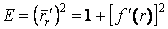 , , 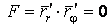 , , 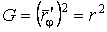 , Линейный элемент , Линейный элемент 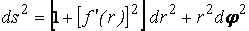 . Так как . Так как 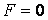 , то координатные линии образуют ортогональную сеть. Линии j=ConstНазываются меридианами (они получаются в сечении поверхности плоскостями, проходящими через ось вращения). Линии R=const называются параллелями (они получаются в сечении поверхности плоскостями, перпендикулярными оси Oz), это окружности с центрами на оси Oz. , то координатные линии образуют ортогональную сеть. Линии j=ConstНазываются меридианами (они получаются в сечении поверхности плоскостями, проходящими через ось вращения). Линии R=const называются параллелями (они получаются в сечении поверхности плоскостями, перпендикулярными оси Oz), это окружности с центрами на оси Oz. | ||||
| 3.5. Вторая квадратичная форма поверхности. Нормальные кривизны. Классификация точек поверхности |  |  |  | |
