Исходные данные к задаче представлены в таблице 1. При использовании метода замены необходимо помнить, что объекты остаются неизменными, меняется положение плоскостей:
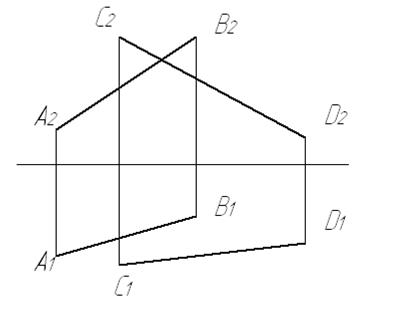
Рисунок 4
Решение:
При использовании метода замены необходимо помнить, что объекты остаются неизменными, меняется положение плоскостей:
-каждая новая плоскость располагается перпендикулярно оставшейся;
-плоскость выбирается так, чтобы проекции объекта заняли частное положение;
- при решении задачи переносятся все объекты.
Кратчайшее расстояние между прямыми – перпендикуляр, проведенный между двумя ближайшими точками прямых. Построить его можно в том случае, если спроецировать одну из прямых в точку. Тогда легко можно найти расстояние между точкой и прямой.
Алгоритм решения задачи следующий:
1 Определяем натуральную величину одного из отрезков. Для этого располагаем новую ось параллельно проекции отрезка.
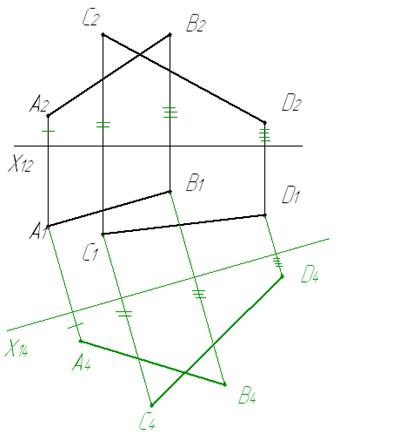
2 Спроецируем прямую так, чтобы она заняла положение проецирующей прямой. Для этого выбираем ось Х2 перпендикулярно натуральной величине отрезка.
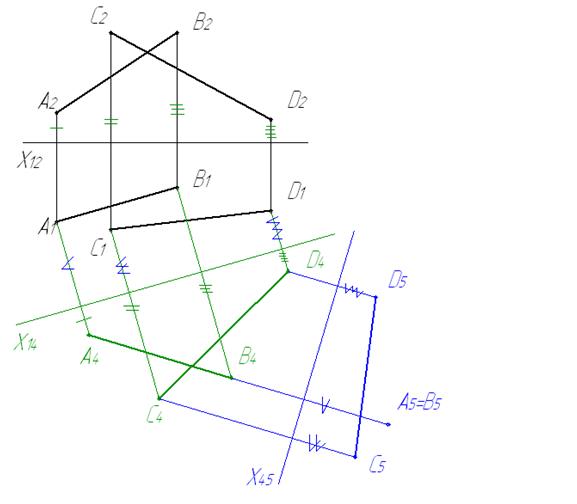
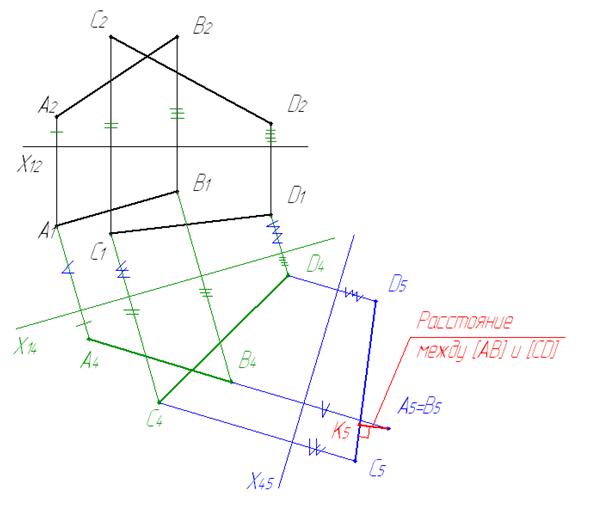
3 Определяем расстояние между двумя прямыми.