Задачи к контрольным заданиям

Строительство – 16з/3,5 - ЗАОЧНОЕ - Теоретическая механика

Фамилия, Имя	Задача С1.	Задача С2
Арькова Наталья	С1.0	С2.0
Бабенко Вадим	С1.1	С2.1
Бариева Дилара	С1.2	С2.2
Бобков Денис	С1.3	С2.3
Богданов Андрей	С1.4	С2.4
Гараев Даниил	С1.5	С2.5
Глазырин Александр	С1.6	С2.6
Глазырина Анна	С1.7	С2.7
Иссомидинов Фируз	С1.8	С2.8
Килина Надежда	С1.9	С2.9
Мансуров Александр	С1.0	С2.0
Матросов Александр	С1.1	С2.1
Миннигалиев Ильнур	С1.2	С2.2
Михайлова Ксения	С1.3	С2.3
Провашинский Алекс-р	С1.4	С2.4
Чикуров Данил	С1.5	С2.5
Чурина Кристина	С1.6	С2.6
Шаймуллин Ринат	С1.7	С2.7
Шакриев Людовик	С1.8	С2.8

Пояснения: Номер варианта соответствует номеру рисунка в задачах С1 и С2.

В таблицах С1 и С2 номер варианта соответствует номеру условия.

В помощь, к каждой задаче рассмотрен подробно пример и алгоритм решения.

Задача С1

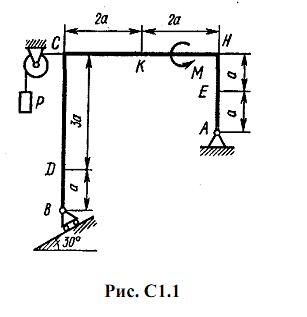
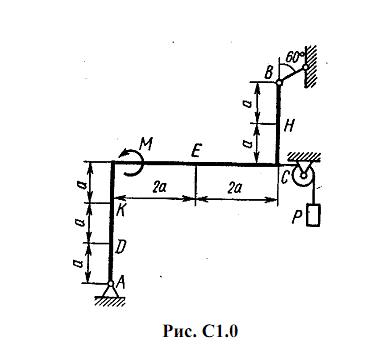
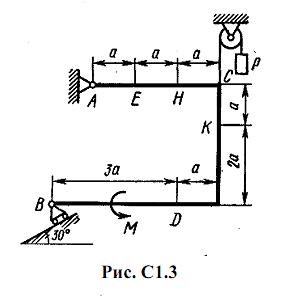
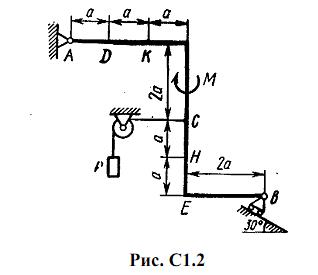
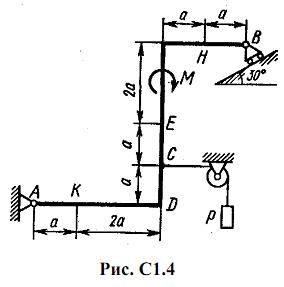
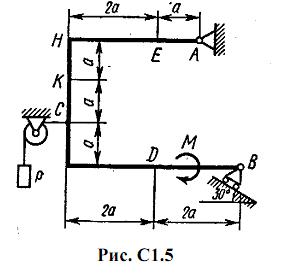
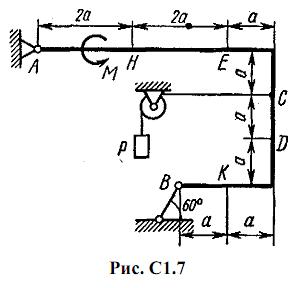
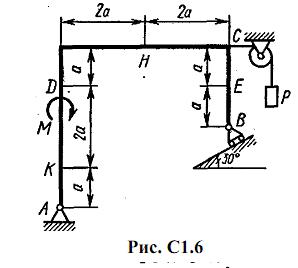
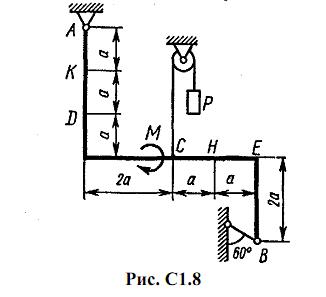
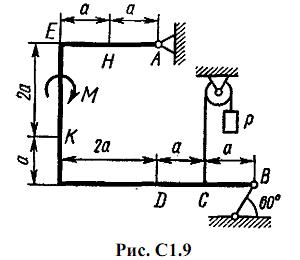
Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0-С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.

В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25 кН. На раму действуют пара сил с моментом М = 100 кН·м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действуют сила F₂ под углом 15° к горизонтальной оси, приложенная в точке D, и сила F₃ под углом 60° к горизонтальной оси, приложенная в точке E, и т. д.).

Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять a = 0,5 м.

Указания. Задача C1 – на равновесие тела под действием произвольной плоской системы сил. При её решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента какой-либо силы F часто удобно разложить её на составляющие F' и F’’ (по правилу параллелограмма), для которых плечи легко определяются; затем применить теорему Вариньона (в алгебраической форме):

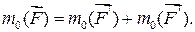
Перед выполнением задания прочтите по учебнику темы: «Основные понятия и аксиомы статики», «Связи и реакции связей», «Плоская система сил», «Пара сил».

Вопросы, на которые следует обратить внимание:

1. Сила, линия действия силы.

2. Проекция силы на ось. В каком случае проекция силы на ось равна нулю?

3. Проекция силы на плоскость, в каком случае эта проекция равна нулю. Отличие проекции силы на плоскость от проекции силы на ось.

4. Алгебраической момент силы относительно центра (точки). В каком случае момент силы относительно центра равен нулю?

5. Что называется связями, перечислите виды связей.

6. Аксиома освобождения от связей.

7. Реакция связи, ее направление и точка приложения.

8. Какая система сил называется плоской (произвольной плоской)? Сформулировать и записать уравнения: условия равновесия плоской системы сил в векторной и алгебраической (координатной) формах.

Пример C1. Жёсткая пластина ABCD (рис. C1) имеет в точке А неподвижную шарнирную опору, а в точке В - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

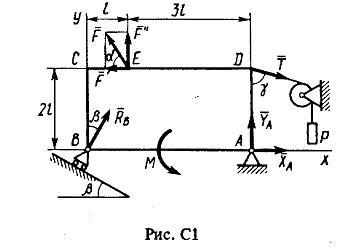
Дано: F = 25 кН, α= 60°, Р = 18 кН, γ= 75°, М = 50 кН·м, β=30⁰, l= 0,5 м.

Определить: реакции в точках А и В, вызываемые действующими нагрузками.

Решение.

Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы (рис. C1):

а) активные силы (нагрузки): силу Fи пару сил с моментом М;

б) реакции связей:

- в точке A связью является неподвижная шарнирная опора, её реакцию изображаем двумя составляющими X_А, Y_А, параллельными координатным осям;

- в точке В связью является подвижная шарнирная опора на катках, её реакция направлена перпендикулярно плоскости опоры катков;

- в точке D связью является трос, реакция троса Tнаправлена вдоль троса от пластины (по модулю Т = Р).

Получилась плоская система сил; составим три уравнения равновесия.

При вычислении момента силы Fотносительно точки А разложим силу Fна составляющие 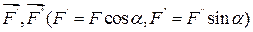и воспользуемся теоремой Вариньона в векторной форме: 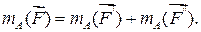Найдём проекцию:

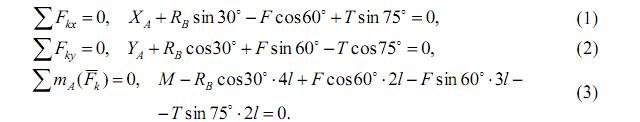
Решение системы уравнений начинаем с уравнения (3), так как оно содержит одну неизвестную R_В:

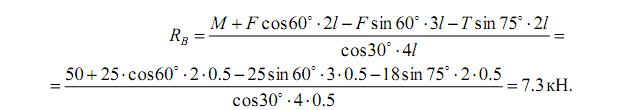
Подставляем R_В в уравнение (1), получим:

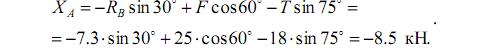
Подставляем R_В в уравнение (2), получим:

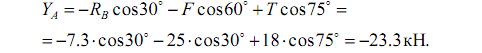
Проверка. Составим, например, уравнение 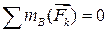(или уравнение моментов относительно любой другой точки (кроме А). Если задача решена верно, то эта сумма моментов должна получиться равной нулю.

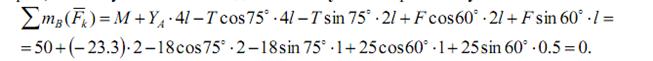Ответ: Х_А = -8,5 кН, Y_A = -23,3 кН, R_B = 7,3 кН. Знаки указывают, что составляющие реакции шарнира X_А и Y_А направлены противоположно показанным на рисунке C1.

В примерах выполнения последующих задач решение уравнений и

проверка не приводятся, но это необходимо делать при выполнении каждой

задачи контрольной работы.

Задача С2

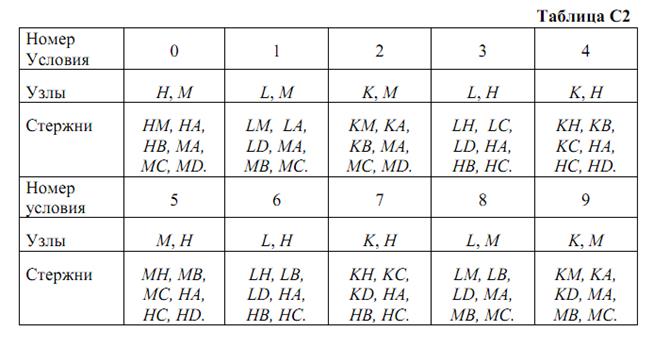
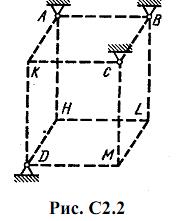
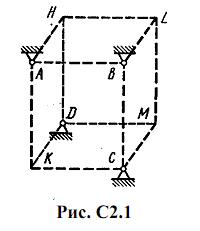
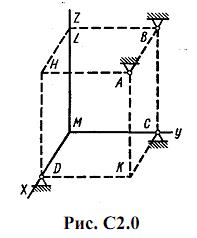
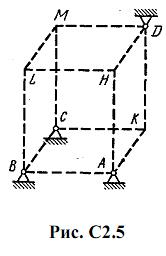
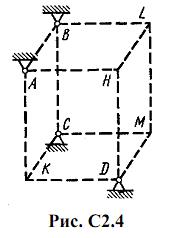
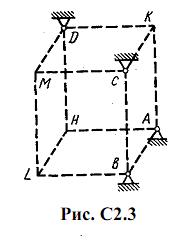
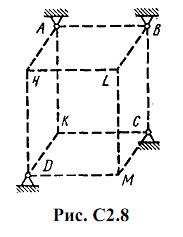
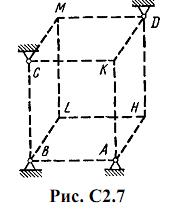
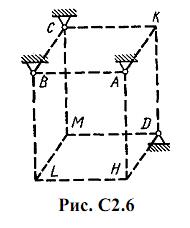
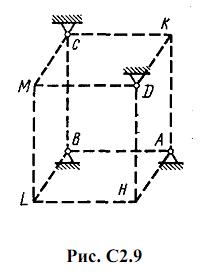
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам А, В, С, D (рис. С2.0-С2.9, табл. С2). Стержни и узлы (узлы расположены в вершинах H, К, L или M прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила P=200 Н; во втором узле приложена сила Q=100 Н. Сила Pобразует с положительными направлениями координатных осей х, y, z углы, равные соответственно α₁=45⁰, β₁=60⁰, γ₁=60⁰, а сила Q – углы α₂=60⁰, β₂=45⁰, γ₂=60⁰; направления осей х, у, z для всех рисунков показаны на рис. С2.0.

Грани параллелепипеда, параллельные плоскости ху, – квадраты. Диагонали других боковых граней образуют с плоскостью ху угол φ=60⁰ , а диагональ параллелепипеда образует с этой плоскостью угол θ=51⁰.

Определить усилия в стержнях.

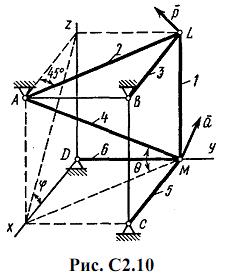
На рис. С2.10 в качестве примера показано, как должен выглядеть чертеж С2.1, если по условиям задачи узлы находятся в точках L и М, а стержнями являются LM, LA, LB; МА, МС, MD. Там же показаны углы φ и θ; при решении своей задачи на рисунке следует указать заданные значения этих углов.

Указания. Задача С2 – на равновесие пространственной системы сходящихся сил. При её решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня.

Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, N₁, N₂ и т.д.).

Перед выполнением задачи С2 дополнительно к теории, указанной к задаче С1, разберите по учебнику тему “Система сходящихся сил”.

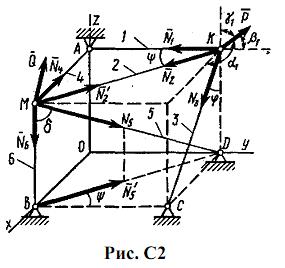
Пример С2. Конструкция состоит из невесомых стержней 1, 2, …, 6, соединенных друг с другом (в узлах К и М) и с неподвижными опорами А, В, С, D шарнирами (рис. С2). В узлах К и М приложены силы Pи Q, образующие с координатными осями углы α₁=60⁰, β₁=60⁰, γ₁=45⁰ и углы α₂=45⁰, β₂=60⁰, γ₂=60⁰ соответственно (на рисунке показаны только углы α₁, β₁, γ₁).

Дано:Р=100 Н, α₁=60⁰, β₁=60⁰, γ₁=45⁰; Q=50 Н, α₂=45⁰, β₂=60⁰, γ₂=60⁰, ψ=30⁰, φ=60⁰, δ=74⁰.

Определить:усилия в стержнях 1-6.

Решение.

1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. На узел действуют:

а) активная сила P;

б) реакции связей (стержней): N₁, N₂, N₃, которые направим по стержням от узла, считая стержни растянутыми. Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:

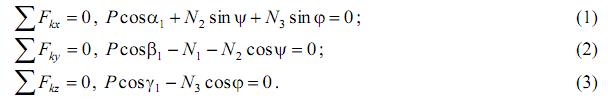
Решив уравнения (1), (2), (3) при заданных числовых значениях силы Р и углов, получим N₁=349 Н, N₂ = -345 Н, N₃ =141 Н.

2. Рассмотрим равновесие узла М. На узел действуют:

а) активная сила Q;

б) реакции связей (стержней): N₂^’, N₄, N₅, N₆. При этом по закону о равенстве действия и противодействия реакция N₂ направлена противоположно N₂.

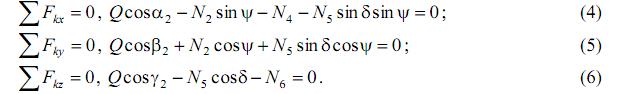Получилась пространственная система сходящихся сил. Составим её уравнения равновесия:

При определении проекций силы N₅ на оси Oх и Oу в уравнениях (4) и (5) удобнее сначала найти проекцию N₅^’ этой силы на плоскость хОу (по числовой величине 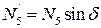), а затем найденную проекцию на плоскость спроектировать на оси Oх, Oу.

Решив систему уравнений (4), (5), (6) и учитывая, что 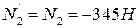, найдем, чему равны N₄, N₅, N₆. Напоминаем, что в своей задаче решение систем уравнений (1)-(3) и (4)-(6) следует выполнить подробно и с пояснениями.

После решения сделайте проверку, составив для любого узла уравнение 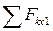, где ось x₁ направьте, например, по диагонали квадрата, расположенного в плоскости xOy. Эта сумма должна получиться равной нулю.

Ответ: N₁=349 Н; N₂ = -345 Н; N₃ =141 Н; N₄=50 Н; N₅ =329 Н; N₆ =-66 Н.

Знаки показывают, что стержни 2 и 6 сжаты, остальные – растянуты.