Пайданылған әдебиеттер

1.Әбілқасымова А. және т.б. Математиканы оқытудың териясы мен әдістемесі. А, Білім. 1998 ж

2. Бидосов Ә. Математиканы оқыту методикасы. (Жалпы методика). А, Мектеп. 1989ж

3. Рахымбек Д. және т.б. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. Ш, 2003

24-лекция.

Математикалық есептер

Жоспары:

1. Есептің математиканы оқытудағы орны және міндеттері

2. Математикалық есеп және оның түрлері;

3. Есепті шығарға қойылатын талаптар

1. Есептің математиканы оқытудағы орны және міндеттері

Математикада ғылым ретінде есептен пайда болған және есеп арқылы дамиды. Тарихқа жүгінсек, ең көне математикалық ескерткіштер Ринд және Мәскеу папирустарында есептер қарастырылып, оларды шығару жолдары берілген. Есеп шығару мұқтаждығын мүмкіндіктер теориясы, ойындар теориясы, информатика теориясы т.б. дамыды.

Мектеп математикасын есепсіз құру мүмкін емес.

Ресейдегі алғашқы “Арифметика” авторы Л.Ф.Магницкий арифметикалық төрт амалды қосуға арналған есептер жүйесін құрастырған. “Мақсатты түрде құрылған есептер әдістемесін” ұсынушы атақты педагог-математик С.И.Шохор-Троцкий үйдің “барлық төрт бұрышына есеп қойылуы керек” деген. Осы кезеңдегі көрнекті әдіскер-ғалым П.М.Эрдинев: “Барлық әдістеме есеп шығару әдістемесіне шоғырлануы керек”, – дейді.

Математикалық есеп оқушылардың ұғымдарды, теорияны және математика әдістерін меңгерудің тиімді де, айырбасталмайтын құралы болып табылады. Оқушылардың ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктіліктері мен дағдыларының қалыптасуында, математиканың практикамен байланысын көрсетуде есептің алатын орны өте зор.

Математиканы оқытудағы басты мақсаттарға жетуге есеп – басты қызметші болып табылады. Сондықтан математика сабақтарының жарты уақыты есеп шығаруға арналады. Әрбір мектеп бітіруші оқушы орта есеппен 15000-дай есеп шығарады екен. Ал солардың көпшілігі жоғары және арнаулы орта оқу орындарына тусу емтихандарында математикадан берілген тапсырмаларды шығара алмай жатады. Бұл әлі де мектеп математикасын оқытуда есеп шығаруға көңіл аз бөлініп отырғандығының дәлелі.

Есептің негізгі міндеттері: оқыту, тәрбиелеу, дамыту және бақылау болып табылады. Барлық есептер оқыту міндетін орындайды. Басқаша айтқанда, кез келген есепті шығарғанда оқушы математикалық білім алады, шығару біліктілігі қалыптасады, дағдыға ие болады, яғни математикалық білім деңгейі жоғарылайды. Көбінесе әр есеп өзінің мазмұны арқылы тәрбиелік міндетін атқарады. Мысалы, қоғам дамуының әр түрлі кезеңдеріне байланысты, есеп мазмұны да өзгеріп отырады. Бір кезеңдерде есептер жинағы көпестердің сауда-саттығын, арзанға сатып алу, керісінше қымбатқа сату, құмарлық ойындарында ұту т.с.с. мазмұнды болды. Қазіргі оқулықтарда есеп мазмұны оқушылардың жоғарғы моральдық қасиеттерін қалыптастыруға, ғылыми көзқарастарын дамытуға, интернационалдық және патриоттық рухта тәрбиелеуге негізделген. Оқушыларды есеп мазмұны арқылы ғана тәрбиелеп қоймайды, оларды есеп шығаруға үйретуде тәрбиелеу болып саналады. Есеп шығару оқушылардың сөйлеу мәдениетіне, мінез-құлқының қалыптасуына, табандылыққа, шыншылдыққа, бастаған істі аяғына дейін жеткізу, қиындықты жеңе білу сияқты қасиеттерінің тәрбиеленуіне ықпалын тигізетіні аян.

Есеп оқушылардың логикалық ойлау, кеңістікті елестету, жеке бас қабілеттерін дамытуға бірден-бір себепші болатын басты құрал болып табылады. Оқушылардың білімін, біліктілігін және дағдысын анықтауды бақылау міндеттері де көбінесе есепке жүктеледі.

2.Математикалық есеп және оның түрлері

Есеп шығару – ерекше жұмыс, дәлірек айтсақ ой жұмысы. Ал кез келген жұмысты дұрыс атқару үшін, оның неден тұратыны және оны орындау үшін қандай құрал, әдіс керек екендігін алдын ала анықтап алу қажет. Кез келген есеп шарттардан және талаптардан құралады.

Есеп: Тікбұрышты үшбұрыштың катеті 5м-ге тең, ал оның гипотенузадағы проекциясы 3м. Гипотенузаны және екінші катетті тап. Есеп шарттарын былай бөліп көрсетуге болады.

а) Тікбұрышты үшбұрыш; ә) бір катеті 5м-ге тең; б) белгілі катеттің гипотенузадағы проекциясы 3м-ге тең. Есеп талабы: а) гипотенузасын және; ә) екінші катетті табу керек. Есеп шартында ұғымдар, қатыстар, теориялар қамтылады. Есеп талабы “дәлелде”, “есепте”, “сал”, “зертте”, “қанша болады” т.с.с. сөздермен айтылады. Есеп шығару дегеніміз не? Мысалдар қарастырайық:

а) 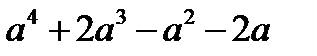(1)

көпмүшелігін көбейткіштерге жікте. Шығару:

1) Қосудың ауыстырымдылық және терімділік заңдары негізінде берілген (1) көпмүшелігін былай жазуға болады:

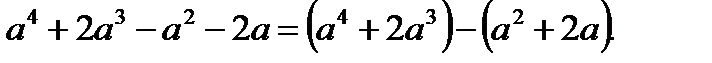(2)

2) Ортақ көбейткішті жақша алдына шығару ережесі бойынша (2)-ні басқаша жазсақ:

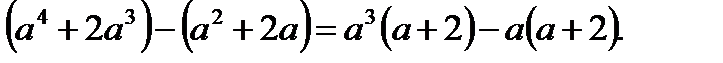(3)

3) Осы ережені тағы бір қолдансақ, (3)-ден

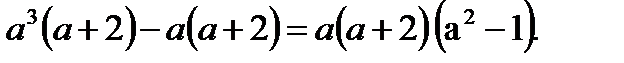(4)

4) Қысқаша көбейту формуласын пайдалансақ

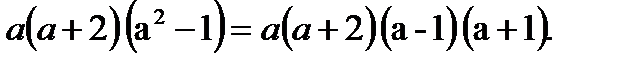
Сонымен

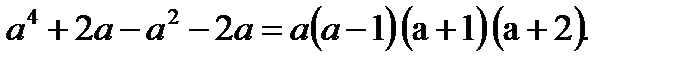
Есеп талабына жауап қайтарылады, есеп шығарылады.

ә) Үшбұрыш қабырғалары 13, 14, 15 болса, оған сырттай сызылған шеңбердің радиусын тап.

Шығару: 1) Герон формуласы бойынша

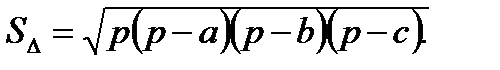
2) 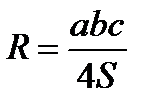формуласы бойынша

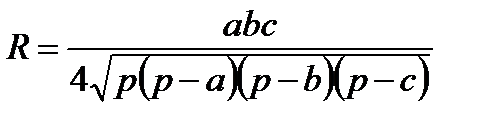
шығады.

3) Сан мәндерін орнына қойсақ

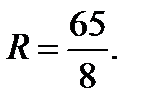
Көрсетілген есептерді шығару кезінде, бұрыннан белгілі қандай да болмасын заңдылықтарды есеп шартына қолдана отырып, есептің талабына жауап ізденіліп отыр. Яғни, есеп шығару дегеніміз – математиканың жалпы заңдылықтарын (анықтамалар, аксиомалар, теоремалар, заңдар, формулалар), есеп шартына немесе оның салдарына белгілі бір ретпен қолдана отырып, есеп талабына жауап беру болып табылады. Сонымен есеп шығару, оның шартына белгілі бір математикалық ережелерді сәйкес түрде қолдана отырып, талабына қарай жылжитын ой қозғалысы. Есеп қарастырылатын объектілеріне байланысты – практикалық және математикалық болып екіге бөлінеді. Яғни есепте қарастырылатын объектінің бірі нақты шын зат болатын болса, ол практикалық есеп. Мысалы, Жер радиусы 6370 км, ал одан 4 км жоғары биіктікте ұшып бара жатқан тікұшақтан қаншалықты алыс жер көруге болады? Есепте қарастырылатын объектілер таза математикалық болса, ол математикалық есеп. Мысалы, М нүктесінен жүргізілген қиюшы шеңберді А және В нүктелерінде қияды, сол нүктеден жүргізілген жанама шеңберді С нүктесінде жанайды. 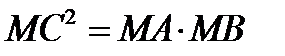болатындығын дәлелде.

Теоремаға байланысты стандартты және стандартты емесесеп түрлері белгілі. Дайын ережелердің көмегімен шығарылатын есеп стандарттық есеп делінеді де, ал шығару жолдары дайын ережелер арқылы табыла қоймайтын есеп – стандарттық емес есеп болады. Мысалы. 1. Егер 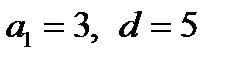болса, арифметикалық прогрессияның алғашқы алты мүшесін жаз (стандарттық есеп). 2. Арифметикалық прогрессияның төртінші мүшесі 4-ке тең. Прогрессия айырымының қандай мәнінде оның алғашқы үш мүшесінің қос-қостан алған көбейтінділерінің қосындысы ең кіші мәнге ие болады (стандартты емес)? Есеп талабына қарай: а) есептеу, ә) дәлелдеу, б) зерттеу, в) салу есептеріне бөлінеді. Есептеуге арналған есептерге: өрнек мәнін табу, функцияның мәнін есептеу, кесіндінің ұзындығын, фигураның ауданын табу, бұрыш шамасын анықтау т.с.с. жатады.

Қандай да болмасын ұйғарымның ақиқаттылығына көз жеткізу немесе ұйғарымның жалғандығын тексеру не белгілі бір құбылыстың дұрыстығын түсіндіру – дәлелдеу есептері.

Теоремалардың барлығын да дәлелдеу есептеріне жатқызуға болады.

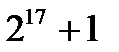“ саны жай сан ба, құрама сан ба?”

“Қандай трапецияның диагоналы оның орта сызығын тең үш бөлікке бөледі”. “а және b-ның қандай мәндерінде

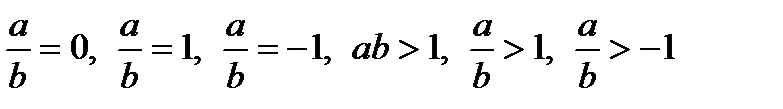
теңдіктері орынды” т.с.с. есептері зерттеуге арналған есептер. Зерттеу көптеген есептер шығару кезінде кездеседі: нүктелердің геометриялық орны, теңдеулер мен теңсіздіктердің шешім сандарының қаншалықты болуы т.с.с.

Белгілі бір құралдар жәрдемімен берілген шарттарды қанағаттандыратын фигуралар салу – салу есептерін құрайды. Есеп шығаруға кіріспес бұрын, оқушыларды есеп түрін анықтап алуға үйрету – басты талаптардың бірі болып табылады.

Өзінің алға қойған дидактикалық мақсаттарына қарай есептерді үш түрге бөлуге болады:

1)танымдық есептер:бұлар арқылы жаңа білім алынады; 2) машықтану есептері: бұлар арқылы орнықты білім дағдылар қалыптасады; 3) шығармашылық ойлауды қажет ететін дамыту есептері.Таным есептерін жаңа материалдар өтуде, оқытудың проблемалық және эвристикалық әдістерін қолдануда шығару керек. Бұл дидактика талаптарына сай келеді, сондықтан математиканы оқып-үйрену барысында кеңінен қолданылады. Алайда мектеп математикасында ең көп тараған есеп түрлері жаттығу есептері болып табылады, олар математикалық білімдерді қолдануда сапалы және берік дағдылар қалыптастыра отырып, математикалық теорияларды саналы түрде меңгеруге ықпал етеді.

Жаттығу және танымдық есептерді шығарумен шектелу, оқушылардың эвристикалық, шығармашылық ойлауын дамытуды толық қамтамасыз ете алмайды. Сондықтан бұл мақсатты жүзеге асыруға математикалық, логикалық, интуициялық, тапқырлық т.б. қабілеттер араласатын арнайы іріктелген есептер шығарып отырудың маңызы аса зор.

Шешу кезінде қандай ойлау түрінің басым болуына байланысты есептерді алгоритмдік, жартылай алгоритмдік және эвристикалық деп шартты түрде үшке бөлуге болады. Танымдық есептер негізінен жартылай алгоритмдік, дамытушы-эвристикалық есептерге жатады. Формула немесе ереже бойынша шығарылатын есептер алгоритмдік және жартылай алгоритмдік болып келеді.

3. Есеп шығаруға қойылатын негізгі талаптар

Есеп шығаруға төмендегідей талаптар қойылады:

а) Қатесіз шығару; ә) негіздеу (дәлелдеу), б) толық шығару; в) мүмкіндігінше тиімді жолмен шығару; г) есепті қаттау (оформление).

а) “Есеп қатесіз шығарылу керек”.

Бұл негізгі талап. Оқушылар есеп шығару кезінде алгоритмдік, логикалық, сызбалық, терминологиялық, шындықты бұрмалау сияқты қателер жіберуі мүмкін. Енді оқушылар жиі жіберетін қателіктерді көрсетелік.

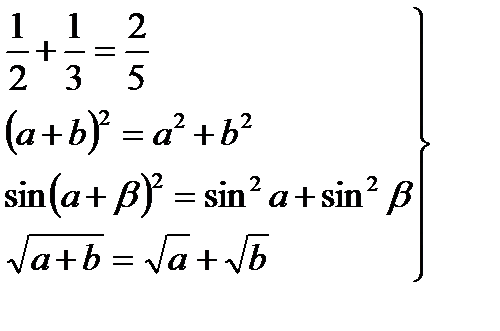– алгоритмдік қателіктер.

5=–5 екендігін дәлелдеу. Екі жағын квадраттаймыз, сонда 25=25

немесе

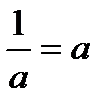
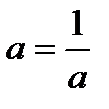
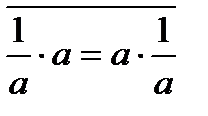
1=1 – логикалық қателік.

Бүйір жақтары квадраттар болатын алты бұрышты дұрыс призманың ішінен төменгі табанының қабырғасы мен жоғарғы табанының оған қарсы жатқан қабырғасы арқылы жазықтық жүргізіңдер. Осы қима тік төртбұрыш ретінде салынса, ол сызбалық қате.

“Бүйір жағының апофемасы”, “шеңбердің ауданы” т.с.с. – терминологиялық қателіктер.

Есеп: “Моторлы қайық өзен ағысымен 42 км және ағысқа қарсы 20 км жол жүріп және оған 5 сағ уақыт жұмсады. Егер өзен ағысының жылдамдығы 2 км/сағ болса, қайықтың өз жылдамдығы қандай?”.

Есеп 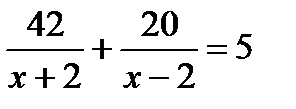теңдеуін құру арқылы шығарылды. Теңдеу түбірлері 2/5 және 12 есеп жауабы ретінде алынса, онда шындықты бұрмалау қателігі жіберілгені. Себебі, қайық жылдамдығы өзен жылдамдығынан артық болуы тиіс, яғни 2/5 есеп шартын қанағаттандырмайды. Жауабы: 12 км/сағ.

ә) Есеп шығару кезеңінің әр сатысы міндетті түрде негізделіп, дәлелденіп отыруы қажет. Яғни әрбір жаңа ой қорытындысы қандай тұжырымнан туындалады, не себепті олай деп пайымдауға хақымыз бар сұрақтарға мұқият жауап берілуі керек.

Мысал. Қыры а-ға тең кубтың төменгі табанының іргелес қабырғаларының ортасынан және жоғарғы табанының олармен бір жағында жатпайтын екі іргелес қабырғаларының орталары арқылы жазықтық жүргізіліген. Қиманың ауданын тап.

Шешуі: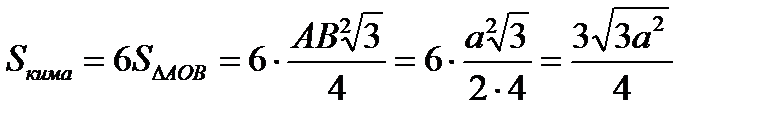

шешуі дұрыс болғанмен, қимадағы алтыбұрыш неге дұрыс екендігін дәлелдеп көрсету керектігі туындайды (15-сурет).

Немесе “дұрыс үшбұрышты пирамиданың бүйір қырлары табан жазықтығымен өзара тең α бұрышын жасайды. Егер пирамиданың бүйір қыры b болса, онда оның биіктігі неге тең болатынын тап”.

Осы пирамиданың төбесі табанға қалай проекцияланатынын дәлелдемей есепті әрі қарай шығару туралы сөз болмағанда болар еді.

б) Теңдеудің бір шешімі дұрыс табылды делік, ал оның әлі екі шешімі бар. Бірден түсінікті, есеп толық шығарылған жоқ, немесе кейде иррационал теңдеулерді шешкенде бөгде түбірлер пайда болуы мүмкін. Егер табылған шешімдердің бәрін теңдеу түбірі десек, есеп толық шығарылмағаны. Зерттеулерге арналған есептерде (әсіресе, геометриялық) мүмкін болатын барлық жағдайлар қарастырылғанда ғана, есеп толық шығарылды деп айта аламыз.

в) Есеп мүмкіндігінше тиімді, ұтымды жолмен шығарылғаны жөн. Мысал ретінде 11-сынып геометриясындағы (А.В.Погорелов) есепті қарастырайық. “Үшбұрышты пирамиданың бүйір қырлары өзара перпендикуляр, олардың әрқайсысы b-ға тең. Пирамида көлемін табыңдар” (16-сурет).

Берілгені: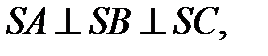

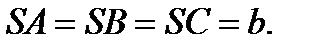
Табу керек:V_{пирамида} – ?

Шешуі:Пирамиданы аударып, табаны ретінде SBC үшбұрышын қарастырсақ, есеп әлдеқайда оңай шығарылады:

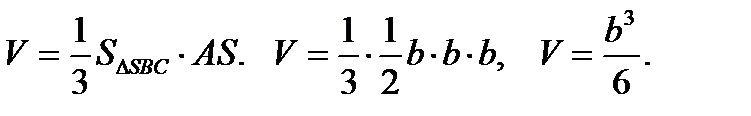
Мысал. 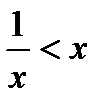теңсіздігінің шешімін табу ұсынылса, әдетте

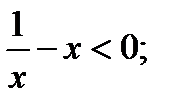
шығару былай жүргізіледі:

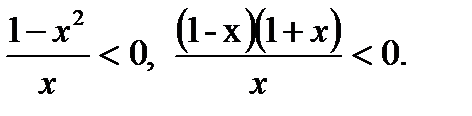
одан әрі интервалдар әдісі қолданылады. Есепті сызбалық тәсілмен шығару, тиімді жолдың бірі болар еді (17-сурет).

Жауабы: (-1;0) (1;+∞)

г) Есеп шығару кезеңдерін дұрыс қаттау да есепке жүктелетін талаптардың бірі болып саналады. Есеп шығару кезеңдері қысқа да нұсқалы, түсінікті, сызбалар қатесіз, дәл т.б. болуы қажет. Геометриялық есептер шығаруда есеп мазмұнына сәйкес ақылға қонымды сызба салынуы керек. Есеп шарттары, талабы айқын көрсетілуі тиіс. Шығару жолдары қысқа түрде, қажет символикаларды пайдаланып жазылуы керек. Әр жаңа тақырыпқа есептер шығарылғанда, мүмкін болатын жазу үлгісі беріліп, ілгеріде соның мұқият сақталуын қадағалаған жөн. Логарифмдік теңдеуді шығару кезеңдерінің жазу үлгісін ұсыналық:

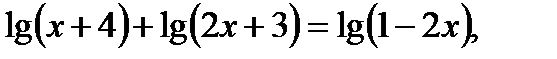
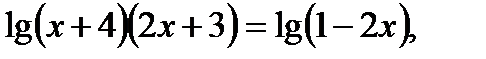
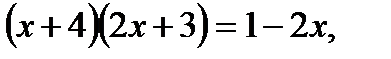
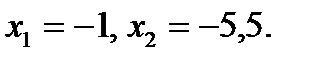
Тексеру 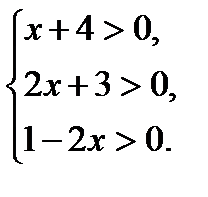(1)

(1)-ге қойсақ, 1) 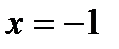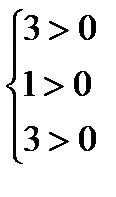– шын

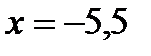
2) 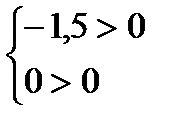– жалған

Жауабы: х=-1

Сұрақтар:

1. Есептің математиканы оқытудағы орны және міндеттері

2. Математикалық есеп және оның түрлері;

3. Есепті шығарға қойылатын талаптар