Первый этап: Определение разности абсолютных давлений в резервуарах

а. Открыв продувочные 9 и рабочие 8 вентили дифференциального манометра выравниваем давление в резервуарах А и Б, сравняв его с атмосферным.

б. Закрываем вентили 7, 8, 9.

в. При помощи ручного насоса создаем разность давлений в резервуарах А и Б, делая 10 оборотов маховика насоса.

В левом резервуаре А создается давление 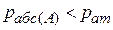, в правом Б – 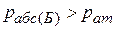(рис. 9).

г. Открываем рабочие вентили 8. Разность уровней в коленах дифманометра 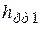, отсчитываемая с помощью визиров 11. Разность абсолютных давлений в резервуарах определяем по формуле:

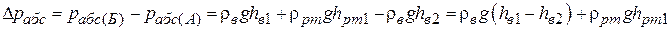
Если h_в1=h_в2, то формула упрощается до вида

,

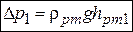где 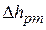– разность уровней ртути в коленах дифманометра;

r_рт – плотность ртути (r_рт = 13600 кг/м³);

r_в – плотность воды (r_в = 1000 кг/м³).

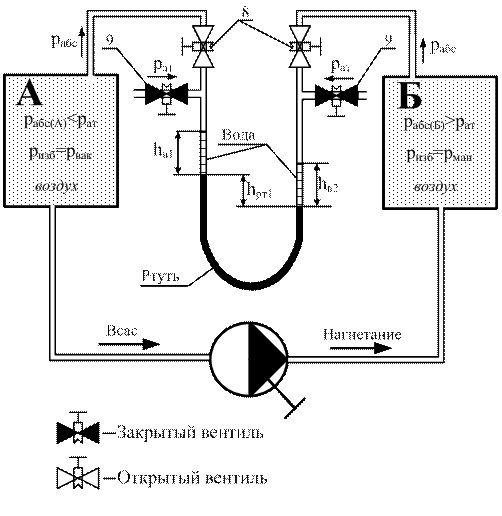Рис. 9. Схема к определению разности абсолютных давлений в резервуарах

Второй этап: Определение манометрического давления в резервуаре Б:

а. Закрываем левый рабочий вентиль 8 и открываем левый продувочный вентиль 9.

б. Разность уровней в коленах дифманометра 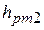отсчитываем опять с помощью визиров 11 (рис. 10). Манометрическое давление в резервуаре Б определяем по формуле:

.

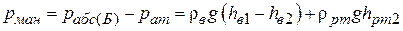При h_в1=h_в2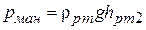

в. Разность между 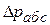и 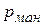дает величину вакуумметрического давления в резервуаре А.

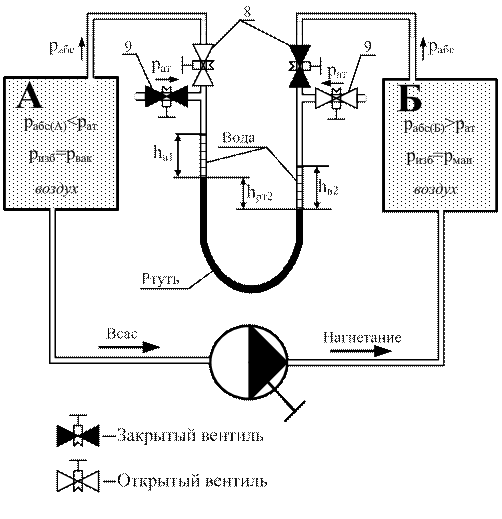Рис. 10. Схема к определению манометрического давления в резервуаре Б

Третий этап: Определение вакууметрического давления в резервуаре А:

а. Закрываем левый продувочный вентиль 9 и снова открываем левый рабочий вентиль 8. Устанавливается первоначальная разность уровней.

б. Закрываем правый рабочий вентиль 8 и открываем продувочный 9. Устанавливается разность уровней 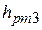, которая покажет нам величину вакуумметрического давления в левом резервуаре (рис.11). Вакууметрическое давление в резервуаре А определяем по формуле:

.

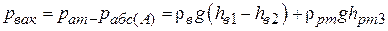При h_в1=h_в2 .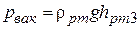

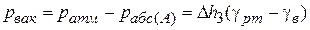
в. Разность 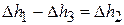дает нам представление о манометрическом давлении в правом резервуаре.

г. Весь опыт повторить, начиная с первого этапа, делая 15 оборотов маховика насоса.

Рис. 11. Схема к определению вакууметрического давления в резервуаре А

Результаты поместить в табл. 2.

Таблица 2

Экспериментальные данные и обработка результатов

Номера опытов

Разность уровней

Определение давления в CИ

Давления р, рман, рвак

hрт1

hрт2

hрт3

Разность абсолютных давлений

Маномет­рическое давление

Вакууммет­рическое давление

кгс/см2

мм вод. ст

мм рт. ст

Таблица 3

Размерность давления

Единицы давления в системах
СИ	СГС	МКГСС	Внесистемные единицы давления
Паскаль (Па)	Дина на квадратный сантиметр (дин/см2)	кгс/м2	физическая (нормальная) атмосфера (атм); техни­ческая атмосфера (ат); миллиметр ртутного столба (мм рт. ст.)

Таблица 4

Связь между единицами давления

Единица	Па	дин/см2	кгс/м2 (мм.вод.ст)	кгс/см2	атм	мм рт. ст
1 Па			0,102	1,02 10-5	9,87	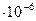7,5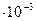
1 дин/см2	0,1		1,02	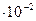1,02	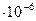9,87	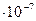7,5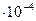
1 кгс/м2	9,81	98,1		10	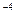9,87	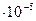7,36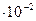
1 кгс/см2	9,81 104	9,81 10-5	10	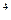	0,968	7,36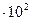
1 атм	1,01	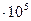1,01	1,03	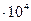1,03		7,6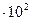
1 мм рт.ст.	1,33	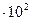1,33	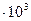13,6	1,36	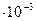1,32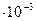

ЛАБОРАТОРНАЯ РАБОТА № 3

«ИССЛЕДОВАНИЕ РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ
В КРУГЛОЙ ТРУБЕ»

Цель работы:

1. Определение значений числа Re при ламинарном и турбулентном движении.

2. Определение критического значения числа Re_кр

Общие сведения

Рядом исследователей (Хагеном в 1839 г., 1854 г., Д.И. Менделеевым в 1880 г.) было отмечено существование принципиально различных режимов движения жидкости. Исследования англичанина Рейнольдса (1883 г.) позволили выяснить сущность этих различий.

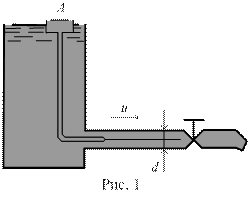
Установка О. Рейнольдса представляла резервуар (см. рис. 1) из которого по стеклянной трубе диаметром d вытекала вода, среднюю скорость υ которой можно было регулировать. В эту трубу из сосуда А по трубке малого диаметра подавалась краска. В результате опытов было установлено:

1) при υ < υ_к краска, перемещаясь с водой, двигается или тонкой струйкой или отдельными слоями. Такое движение было названо ламинарным;

2) при υ > υ_к краска равномерно распределяется по всему объему жидкости. Движение частиц жидкости в этом случае носит неустановившийся характер и называется турбулентным.

Скорость υ_к, при которой в данной трубе происходила смена режимов движения, была названа критической.

О. Рейнольдс установил, что в трубах различного диаметра для жидкостей с различной вязкостью смена режимов осуществляется при одном и том же значении безразмерного комплекса критерия Рейнольдса Re определяемого по формуле:

,

где d – диаметр трубопровода;

n – кинематический коэффициент вязкости жидкости.

Скорость, при которой происходит переход турбулентного режима в ламинарный, называется нижней критической скоростью 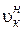, а число Рейнольдса, соответствующее критической скорости называется критическим числом 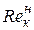и принимает значение 2320:

.

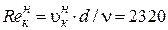В случаях, когда живое сечение потока отличается от круглого, а так же при наличии близко расположенных местных сопротивлений (вентилей, поворотов, золотников, клапанов и т.д.) может быть меньше 2320.

Но учитывая, что 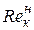найденное для 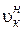всегда меньше или равно 2320, это значение принимается при расчетах за критическое.

Таким образом, для Re < 2320 движение принято считать ламинарным, а для Re > 2320 – турбулентным.

При различных режимах движения имеют место различные зависимости между потерями напора и средними скоростями движения. При ламинарном движении потери напора пропорциональны первой степени скорости, с при турбулентном – скорости в степени m, причем 1,75 < m < 2.