Дніпропетровський національний університет імені олеся гончара
Форма №3
| Предметом дослідження кібернетики є: | а | б | в | г | в | |
| а)процеси управління в неживій природі; | ||||||
| б)процеси управління в економічних системах; | ||||||
| в)процеси управління в складних динамічних системах; | ||||||
| г) всі відповіді вірні. | ||||||
| Емерджентність – це: | а | б | в | г | г | |
| а)властивість системи підтримувати деякі параметри в допустимих межах; | ||||||
| б)визначення поведінки складного об’єкта як результату об’єднання властивостей систем, з яких він складається; | ||||||
| в)всі відповіді вірні; | ||||||
| г) ефект взаємодії, що не є сумою локальних ефектів. | ||||||
| Концепція «чорної скрині» полягає в тому, що: | а | б | в | г | а | |
| а)досліджується система, внутрішня структура якої невідома, або остання не є предметом вивчення; | ||||||
| б)система розглядається як абсолютно замкнена, що не має взаємодії з зовнішнім середовищем; | ||||||
| в)дослідження системи виконується у відповідності з принципами системного підходу; | ||||||
| г) всі відповіді вірні. | ||||||
| Одиниця вимірювання інформації «біт» – це: | а | б | в | г | г | |
| а)) ступінь невизначеності системи, яка може знаходитися тільки у двох станах; | ||||||
| б)невизначеність, що міститься в одній спробі, що має два рівноймовірних результати; | ||||||
| в)кількість ентропії системи , що складається з двох елементів; | ||||||
| г) всі відповіді вірні. | ||||||
| Хто з вчених писав про кібернетику «…И обеспечивает гражданам возможность наслаждаться миром»: | а | б | в | г | б | |
| а)Н.Вінер; | ||||||
| б)А.Ампер; | ||||||
| в)Платон; | ||||||
| г) Трентовський. | ||||||
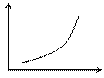 Яким умовам задовольняє виробнича функція, графік якої зображено на малюнку? Яким умовам задовольняє виробнича функція, графік якої зображено на малюнку? | а | б | в | г | а | |
| а)а)f '(x) > 0 і f ''(x) > 0; | ||||||
| б)б)f '(x) > 0 і f ''(x) < 0; | ||||||
| в)f '(x) < 0 і f ''(x) > 0; | ||||||
| г) f '(x) < 0 і f ''(x) < 0; | ||||||
Яка з наведених виробничих функцій є неявною функцією від 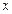 та та 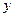 ? ? | а | б | в | г | б | |
а)а) 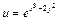 ; ; | ||||||
б) 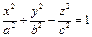 | ||||||
в) 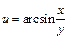 | ||||||
г) 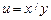 | ||||||
| Яка з наведених функцій задає рівняння еліпса: | а | б | в | г | а | |
а) 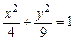 ; ; | ||||||
б) 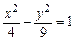 ; ; | ||||||
в) 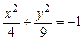 ; ; | ||||||
г) 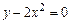 . . | ||||||
Яка з наведених виробничих функцій є неявною функцією від 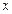 та та 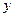 ? ? | а | б | в | г | г | |
а) 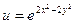 ; ; | ||||||
б) 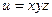 ; ; | ||||||
в) 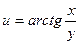 | ||||||
г) 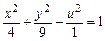 . . | ||||||
Гранична ефективність ресурсу  виробничої функції виробничої функції 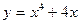 : : | а | б | в | г | а | |
| а) зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)спадає на 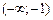 та зростає на та зростає на 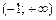 ; ; | ||||||
| г) немає вірної відповіді. | ||||||
| а | б | в | г | |||
| а) | ||||||
| б) | ||||||
| в) | ||||||
| г) | ||||||
Гранична ефективність ресурсу 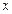 виробничої функції виробничої функції 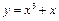 : : | а | б | в | г | г | |
| а)зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)зростає на 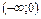 та спадає на та спадає на 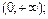 | ||||||
г) спадає на 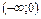 та зростає на та зростає на 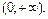 | ||||||
Виробнича функція 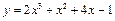 | а | б | в | г | а | |
| а)зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)зростає на 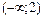 та спадає на та спадає на 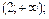 | ||||||
г) спадає на 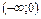 та зростає на та зростає на 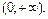 | ||||||
Виробнича функція 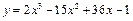 | а | б | в | г | в | |
| а)зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)зростає на 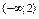 та та 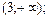 | ||||||
г) спадає на 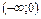 та зростає на та зростає на 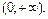 | ||||||
Виробнича функція 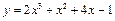 | а | б | в | г | а | |
| а)зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)зростає на 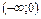 та спадає на та спадає на 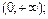 | ||||||
г) спадає на 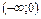 та зростає на та зростає на 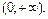 | ||||||
Гранична ефективність ресурсу 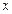 виробничої функції виробничої функції 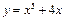 | а | б | в | г | г | |
| а)зростає на усій числовій прямій; | ||||||
| б)спадає на усій числовій прямій; | ||||||
в)зростає на 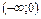 та спадає на та спадає на 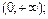 | ||||||
г) спадає на 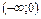 та зростає на та зростає на 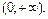 | ||||||
Скільки точок перегину має виробнича функція 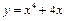 | а | б | в | г | а | |
| а)ні одної; | ||||||
| б)одну; | ||||||
| в)дві; | ||||||
| г) більше двох. | ||||||
Скільки точок перегину має виробнича функція 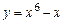 : : | а | б | в | г | а | |
| а)ні одної; | ||||||
| б)одну; | ||||||
| в)дві; | ||||||
| г) більше двох. | ||||||
Для диференційованої функції 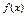 достатні умови опуклості (опуклості доверху): достатні умови опуклості (опуклості доверху): | а | б | в | г | г | |
| а)f '(x) > 0; | ||||||
| б)f '(x)< 0 ; | ||||||
| в)f ''(x) > 0 ; f '(x) < 0; | ||||||
| г) f ''(x) < 0 | ||||||
Для диференційованої функції 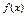 достатні умови вгнутості (опуклості донизу): достатні умови вгнутості (опуклості донизу): | а | б | в | г | в | |
| а) f '(x) > 0; | ||||||
| б)f '(x)< 0 ; | ||||||
| в)f ''(x) > 0 ; | ||||||
| г) f ''(x) < 0, f '(x) < 0. | ||||||
Значення граничної ефективності 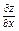 функції функції 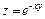 у точці у точці 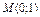 дорівнює: дорівнює: | а | б | в | г | а | |
| а)(-1); | ||||||
| б)2; | ||||||
| в)1; | ||||||
| г) 0; | ||||||
Для яких виробничих функцій зміна граничної ефективності ресурсу 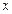 при збільшенні витрат ресурсу при збільшенні витрат ресурсу 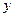 дорівнює дорівнює 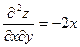 | а | б | в | г | в | |
а) 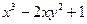 ; ; | ||||||
б) 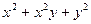 ; ; | ||||||
в) 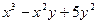 ; ; | ||||||
г) 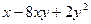 . . | ||||||
Для яких виробничих функцій зміна граничної ефективності ресурсу 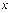 при збільшенні витрат ресурсу при збільшенні витрат ресурсу 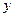 дорівнює дорівнює 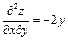 | а | б | в | г | г | |
а) 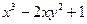 ; ; | ||||||
б) 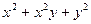 ; ; | ||||||
в) 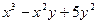 ; ; | ||||||
г) 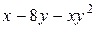 . . | ||||||
Вкажіть точки екстремуму непереривної на усій числовій прямій функції 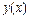 , якщо , якщо 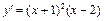 : : | а | б | в | г | б | |
а) 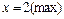 ; ; | ||||||
б) 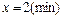 ; ; | ||||||
в) 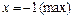 ; ; | ||||||
г) 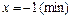 . . | ||||||
Значення граничної ефективності 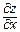 ресурсу ресурсу 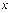 виробничої функції виробничої функції 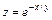 у точці у точці 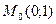 дорівнює: дорівнює: | а | б | в | г | а | |
| а)(-1) ; | ||||||
| б)2; | ||||||
| в)1; | ||||||
| г) 0. | ||||||
Граничні ефективності ресурсів 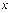 та та 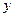 виробничоїфункції виробничоїфункції 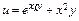 у точці у точці 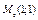 дорівнюють: дорівнюють: | а | б | в | г | в | |
а) 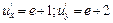 ; ; | ||||||
б) 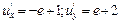 ; ; | ||||||
в) 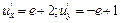 ; ; | ||||||
г) 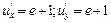 . . | ||||||
Граничні ефективності ресурсів 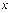 та та 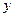 виробничої функції виробничої функції 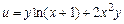 у точці у точці 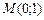 дорівнюють: дорівнюють: | а | б | в | г | а | |
а) 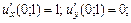 | ||||||
б) 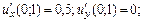 | ||||||
в) 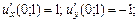 | ||||||
г) 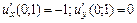 . . | ||||||
Граничні ефективності ресурсів 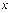 та та 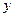 виробничої функції виробничої функції 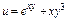 у точці у точці 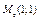 дорівнюють: дорівнюють: | а | б | в | г | в | |
а) 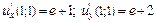 ; ; | ||||||
б) 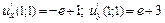 ; ; | ||||||
в) 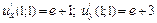 ; ; | ||||||
г)  | ||||||
| Визначник не зміниться, якщо: | а | б | в | г | б | |
| а) замінити елементи першого стовпчика на їх алгебраїчні доповнення; | ||||||
| б)до першого рядка додати другий рядок; | ||||||
| в)змінити місцями перший та другий стовпчики; | ||||||
| г) другий рядок помножити на два та додати до нього перший рядок . | ||||||
| Визначник не зміниться, якщо: | а | б | в | г | б | |
| а)два рядки змінити місцями; | ||||||
| б)до першого рядка добавити другий; | ||||||
| в)перший рядок помножити на два та додати до нього другий рядок; | ||||||
| г) немає вірної відповіді. | ||||||
| Визначник не зміниться, якщо: | а | б | в | г | а | |
| а)від першого рядка відняти третій рядок; | ||||||
| б)замінити елементи першого стовпчика на їх мінори; | ||||||
| в)елементи першого стовпчика помножити на два; | ||||||
| г) другий рядок помножити на три та додати до нього перший рядок. | ||||||
| Визначник дорівнює нулю, якщо: | а | б | в | г | а | |
| а)перший рядок дорівнює різниці двох інших рядків; | ||||||
| б)він містить рядок, у якому усі елементи дорівнюють нулю крім одного; | ||||||
| в)він містить два стовпчики, при зміні яких місцями визначник змінює знак; | ||||||
| г) він містить рядок, у якому сума елементів дорівнює нулю. | ||||||
Нехай матриця A має розмірність т´п , а матриця B — розмірність п´k (m 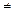 k). Тоді: k). Тоді: | а | б | в | г | а | |
а)розмірність матриці-добутку C=AB буде дорівнювати т´k, елементи її 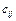 обраховуються за формулою обраховуються за формулою 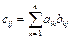 ; ; | ||||||
б)розмірність матриці-добутку C=AB буде дорівнювати n´k, елементи її 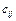 обраховуються за формулою обраховуються за формулою 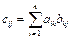 ; ; | ||||||
| в)розмірність матриці-добутку C=AB буде дорівнювати n´n; | ||||||
| г) добуток AB не визначений. | ||||||
| Якщо визначник системи п лінійних рівнянь з п невідомими дорівнює нулю, то: | а | б | в | г | в | |
| а)система не має розв’язків; | ||||||
| б)система має нескінченну множину розв’язків ; | ||||||
| в)система або несумісна, або має нескінченну множину розв’язків; | ||||||
| г) система завжди має хоча б один розв’язок. | ||||||
| Нехай n та p відповідно означають кількість випробувань та ймовірність “успіху” в одному випробуванні у схемі Бернулі, причому n достатньо велике. Тоді має місце твердження: | а | б | в | г | а | |
а)якщо 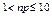 , то ймовірність к “успіхів” можливо знайти використовуючи теорему Пуасона; , то ймовірність к “успіхів” можливо знайти використовуючи теорему Пуасона; | ||||||
б)якщо 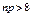 , то ймовірність к “успіхів” можливо знайти використовуючи локальну теорему Муавра-Лапласа; , то ймовірність к “успіхів” можливо знайти використовуючи локальну теорему Муавра-Лапласа; | ||||||
в)ймовірність к “успіхів” можливо знайти використовуючи формулу 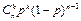 ; ; | ||||||
г) середнє число “успіхів” дорівнює 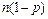 . . | ||||||
| П’ять чотирьохмірних векторів: | а | б | в | г | б | |
| а)можуть бути як лінійно незалежні, так і лінійно залежні; | ||||||
| б)завжди лінійно залежні; | ||||||
| в)завжди лінійно незалежні; | ||||||
| г) лінійно залежні тільки тоді, коли серед них є нульовий вектор. | ||||||
| Для ймовірності події має місце властивість: | а | б | в | г | б | |
| а)ймовірність суми двох довільних подій дорівнює сумі ймовірностей цих подій; | ||||||
| б)ймовірність добутку двох подій не завжди дорівнює добутку ймовірностей цих подій; | ||||||
| в)ймовірність різниці двох подій дорівнює різниці ймовірностей цих подій ; | ||||||
| г) ймовірність добутку несумісних подій дорівнює добутку ймовірностей цих подій. | ||||||
| Фермер приїхав до міста, щоб отримати кредит в одному з банків. Відомо, що ймовірність того, що будь-який банк надасть йому кредит, дорівнює 0,2. Фермер планує звернутися в три банки з метою, вразі згоди, ознайомитися з умовами кредитування. Має місце твердження: | а | б | в | г | а | |
| а) ймовірність того, що усі банки відмовлять фермеру надати кредит більша ніж 0,5; | ||||||
| б)ймовірність того, що два банки згодні надати фермеру кредит, більша ніж 0,1; | ||||||
| в)ймовірність того, що хоча б один банк згодиться надати фермеру кредит, більша ніж 0,4; | ||||||
| г) немає вірної відповіді. | ||||||
| На полиці розташовані папки зі звітами про доходи двох приватних підприємств та трьох страхових компаній. Податковий інспектор навмання бере з полиці дві папки. Подія А –"обрані папки належать страховим компаніям", а подія В – "обрані папка страхової компанії та папка підприємства". | а | б | в | г | а | |
| а)події А та В несумісні; | ||||||
| б)події А та В незалежні; | ||||||
| в)ймовірність того, що хоча б одна з подій А та В відбудеться, більша суми ймовірностей цих подій; | ||||||
| г) немає вірної відповіді. | ||||||
| Якщо фірма невчасно виконує ремонт приладу, то вона платить штраф. Ймовірність цієї події дорівнює 0,1. За тиждень фірмі потрібно зробити ремонт трьох приладів. | а | б | в | г | б | |
| а)ймовірність того, що вона не заплатить штраф, менша ніж 0,7; | ||||||
| б)ймовірність того, що вона заплатить штраф двічі, більша ніж 0,02; | ||||||
| в)ймовірність, що вона тільки один раз заплатить штраф, більша ніж 0,3. | ||||||
| г) немає вірної відповіді. | ||||||
| Фермер приїхав до міста, щоб отримати кредит в одному з банків. Відомо, що ймовірність того, що будь-який банк надасть йому кредит, дорівнює 0,2. Фермер планує звернутися в три банки з метою вразі згоди ознайомитися з умовами кредитування. Має місце твердження: | а | б | в | г | б | |
| а)ймовірність, що усі банки відмовлять фермеру, менша 0,5; | ||||||
| б)ймовірність того, що два банки згодні надати фермеру кредит, менша 0,1; | ||||||
| в)ймовірність, що тільки один банк згоден надати фермеру кредит менша 0,3; | ||||||
| г) немає вірної відповіді. | ||||||
| Відомо, що серед клієнтів банка, що беруть кредит, 30% просять кредит на невелику суму, 50% – на середню та 20% на велику. У банку було обслуговувано два клієнта, які звернулися за кредитом. Відомо, що серед клієнтів банка, що беруть кредит, 30% просять кредит на невелику суму, 50% – на середню та 20% на велику. У банку було обслуговувано два клієнта, які звернулися за кредитом. | а | б | в | г | а | |
| а)ймовірність, що обидва вони звернулися за кредитом на невелику суму, більша ніж 0,08; | ||||||
| б)ймовірність, що тільки один з них звернувся за кредитом на невелику суму, більша ніж 0,5; | ||||||
| в)ймовірність, що один з них звернувся за кредитом на невелику суму, а другий на середню, більша ніж 0,4; | ||||||
| г) немає вірної відповіді. | ||||||
| Підприємець хоче отримати кредит в одному з трьох банків. Відомо, що ймовірність того, що будь-який банк надасть йому кредит, дорівнює 0,1. Має місце твердження: | а | б | в | г | г | |
| а)ймовірність, що усі банки відмовлять підприємцю, більша 0,8; | ||||||
| б)ймовірність того, що тільки два банки згодні надати підприємцю кредит, дорівнює 0,095; | ||||||
| в)ймовірність того, що тільки один банк згоден надати підприємцю кредит, більша ніж 0,4; | ||||||
| г) немає вірної відповіді. | ||||||
| Відомо, що серед клієнтів банка, які відкривать депозит, або беруть кредит, ймовірність того, що такий клієнт відкриє депозит, дорівнює 0,6, а ймовірність того, що він хоче взяти кредит – 0,4. У банку було обслуговувано два клієнта, кожен з яких виконав одну з цих операцій. | а | б | в | г | а | |
| а)ймовірність, що обидва вони відкрили депозит, більша ніж 0,3 | ||||||
| б)ймовірність, що тільки один з них відкрив депозит, більша ніж 0,5; | ||||||
| в)ймовірність, що хоча б один з них відкрив депозит, більша ніж 0,9; | ||||||
| г) немає вірної відповіді. | ||||||
| На полиці розташовані папки зі звітами про доходи одного приватного підприємства та трьох страхових компаній. Податковий інспектор навмання бере з полиці папку. | а | б | в | г | в | |
| а)ймовірність, що обрана папка належить страховій компанії, дорівнює 0,25; | ||||||
| б)ймовірність, що обрана папка страхової компанії менша 0,4; | ||||||
| в)ймовірність, що обрана папка підприємства, дорівнює 0,25; | ||||||
| г) немає вірної відповіді. | ||||||
| Функція розподілу випадкової величини: | а | б | в | г | в | |
| а)приймає значення у проміжку [-1,1]; | ||||||
| б)визначена на проміжку [0, 1]; | ||||||
| в)неперервна зліва; | ||||||
г) приймає значення у проміжку [0, 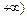 . . | ||||||
| Ймовірність того, що клієнт вчасно поверне отриманий від банка кредит, дорівнює 0,8. Банк за день надав кредити трьом клієнтам. | а | б | в | г | б | |
| а)ймовірність того, що серед цих клієнтів тільки один не поверне вчасно кредит, більша 0,4; | ||||||
| б)ймовірність того, що серед цих клієнтів тільки два не повернуть вчасно кредит, менша, ніж 0,1; | ||||||
| в)ймовірність того, що усі клієнти вчасно повернуть кредит, менша ніж 0,5; | ||||||
| г) немає вірної відповіді. | ||||||
| У коробці декілько деталей, серед яких є браковані. Робітник бере дві деталі. Подія А - {серед деталей одна бракована}, подія В - {серед деталей немає бракованих}. Тоді: | а | б | в | г | в | |
| а) ймовірність того, що серед деталей не більше однієї бракованої, дорівнює добутку ймовірностей подій А та В; | ||||||
| б)події А та В сумістні; | ||||||
| в)ймовірність того, що серед деталей не більше однієї бракованої, дорівнює сумі ймовірностей подій А та В; | ||||||
| г) немає вірної відповіді. | ||||||
| Ймовірність, що клієнт отримує відправлену йому SMS, дорівнює 0,9. Менджер банка відправив SMS трьом клієнтам. Тоді: | а | б | в | г | б | |
| а)ймовірність того, що усі ці клієнти отримують відправлені SMS, більша ніж 0,8. | ||||||
| б)ймовірність того, що тільки два клієнти отримують відправлені SMS, менша ніж 0,25; | ||||||
| в)ймовірність, що тільки один клієнт отримують SMS, більша ніж 0,1. | ||||||
| г) немає вірної відповіді. | ||||||
Нехай 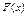 та та 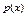 відповідно функція розподілу та функція щільності розподілу випадкової величини . Ймовірність, що випадкова величина попаде до проміжку [а, в] дорівнює: відповідно функція розподілу та функція щільності розподілу випадкової величини . Ймовірність, що випадкова величина попаде до проміжку [а, в] дорівнює: | а | б | в | г | а | |
а)різниці 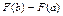 ; ; | ||||||
б)різниці 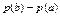 ; ; | ||||||
в) 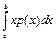 ; ; | ||||||
| г) ймовірності, що випадкова величина попаде до проміжку [0, b-а ]; |
