Взаимное расположение двух прямых в пространстве. Расстояние между прямыми

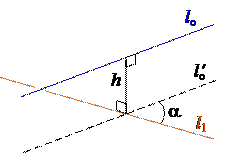Напомним, что углом между скрещивающимися прямыми называется угол между параллельными им прямыми, проходящими через одну точку. Другими словами, если прямые l_o и l₁ скрещиваются, то мы должны совершить параллельный перенос прямой l_o, так чтобы получилась прямая l_o¢ , пересекающаяся с l₁, и измерять угол между l_o¢ и l₁.

Две скрещивающиеся прямые имеют единственный общий перпендикуляр. Его длина называется расстоянием между прямыми.

Пусть две прямые в пространстве заданы своими каноническими уравнениями:

l_o: = = , l₁: = = . (35)

Тогда сразу можем сделать вывод, что (a₁, a₂, a₃)½½ l_o, (b₁, b₂, b₃)½½ l₁, A_o(x_o, y_o, z_o)Î l_o, A₁(x₁, y₁, z₁)Î l₁. Составим матрицу

x₁– x_o y₁– y_o z₁– z_o

A = a₁ a₂ a₃,

b₁ b₂ b₃

и пусть D = detA.

Теорема 8. 1.Угол между l и p вычисляется по формуле

cos a = = . (36)

2.Прямые l_o и l₁ скрещиваются Û D ≠ 0.

3. Прямые l_o и l₁ пересекаются Û D = 0 и не коллинеарен .

4.l_o½½ l₁ Û rank A = 2 и ½½ .

5.l_o= l₁ Û rank A = 1.

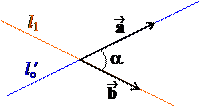Доказательство. 1.Угол a между прямыми l_o и l₁ может быть равен углу b между их направляющими векторами , , а может быть смежным с ним. В первом случае

cos a = cos b = ,

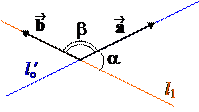а во втором случае

cos a = – cos b =½ cos b½ = .

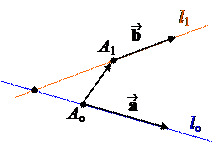Эта формула подойдет и к первому случаю. Обратите внимание, что на чертеже изображена не прямая l_o, а параллельная ей прямая l_o¢ .

2, 3.Очевидно, что прямые l_o и l₁ не параллельны тогда и только тогда, когда их направляющие векторы и не коллинеарны. При этом, прямые лежат в одной плоскости и пересекаются Û векторы , , компланарны Û их смешанное произведение равно нулю: = 0. А в координатах это произведение точности равно D .

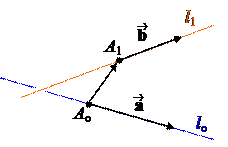Соответственно, если D ≠ 0, то векторы , , не компланарны, а значит, прямые l_o и l₁ не лежат в одной плоскости Þ они скрещиваются.

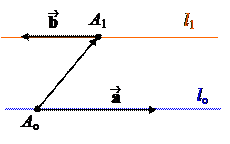4, 5.Если l_o½½ l₁ или l_o= l₁, то ½½ . Но в первом случае вектор неколлинеарен и , и поэтому первая строка в матрице Aнепропорциональна второй и третей строкам. Значит, rank A = 2.

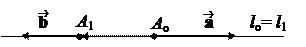Во втором случае все три вектора , , коллинеарны друг другу, и поэтому, все строки

в матрицеA пропорциональны. Значит, rank A = 1.

И обратно, если ||, то прямые l_o и l₁ параллельны или совпадают; при этом, вторая и третья строки матрицы A пропорциональны. Если, при этом, rank A = 2, то первая строка матрицы непропорциональна второй и третьей, а значит, вектор неколлинеарен и Û l_o|| l₁. Если же rank A = 1, то все строки в матрицеAпропорциональны, а значит, все три вектора , , коллинеарны друг другу Û l_o= l₁.

Теорема 9. Пусть две прямые l_o и l₁ в пространстве заданы своими каноническими уравнениями (35). Тогда

1. если l_o½½ l₁ , то расстояние между l_o и l₁ находится по формуле

h = , (37)

2. если l_o и l₁ скрещиваются, то расстояние между ними находится по формуле

h = . (38)

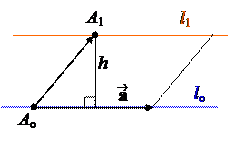
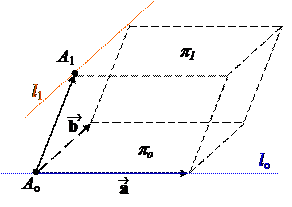Доказательство. 1.Пусть l_o½½ l₁. Отложим вектор от точки A_o, и на векторах и построим параллелограмм. Тогда его высота h будет расстоянием между l_o и l₁. Площадь этого параллелограмма: S =½ ´½ , а основание равно ½ ½. Поэтому

h = S/½ ½ = (37).

2.Пусть l_o и l₁ скрещиваются. Проведем через прямую l_o плоскость p_o½½ l₁, а через прямую l₁ проведем плоскость p₁½½ l_o.

Тогда общий перпендикуляр к l_o и l₁ будет общим перпендикуляром к p_o и p₁. Отложим векторы и из точки A_o и на векторах , и построим параллелепипед. Тогда его нижнее основание лежит в плоскости p_o, а верхнее – в плоскости p₁. Поэтому высота параллелепипеда будет общим перпендикуляром к p_o и p₁, а ее величина h будет расстоянием между l_o и l₁. Объем параллелепипеда равен ½ ½, а площадь основания – ½´½ Þ

h = V/S_осн = (38).

Следствие. Расстояние от точки A₁(x₁, y₁, z₁) до прямой l, заданной уравнением

l: = =

вычисляется по формуле (37).

Примеры решения задач.

1. Даны координаты вершин A(1,– 6), B(–3, 0), C(6, 9) треугольника ABC. Составить уравнение окружности описанной вокруг треугольника.

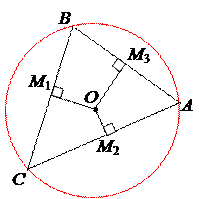Решение. Для того, чтобы составить уравнение окружности нам необходимо знать ее радиус R и координаты центра О(a, b). Тогда уравнение выглядит так:

(x–a)² +(y–b)² = R² .

Центр окружности, описанной вокруг треугольника находится на пересечении серединных перпендикуляров к сторонам этого треугольника. Находим координаты середин M₁(x₁, y₁), и M₃(x₃, y₃) сторон BC и AB соответственно:

x₁= = = , y₁= = = , M₁ .

Аналогично M3(–1,–3).

Пусть l₃ – прямая, являющаяся серединным перпендикуляром к AB , а l₁ – к BC. Тогда = (– 4, 6) ^ l₃ и l₃ проходит через M₃ . Поэтому ее уравнение:

– 4(x+1) + 6(y+3) = 0.

Аналогично = (9, 9) ^ l₃ . Поэтому уравнение l₁:

9(x - ) + 9(y - ) = 0

x + y – 6 = 0.

Имеем О = l₁ I l₃. Поэтому, чтобы найти координаты точки О необходимо решить совместно уравнения l₁ и l₃ :

x + y – 6 = 0 ,

– 4x + 6y +14 = 0.

Прибавим ко второму уравнению первое, умноженное на 4:

x + y – 6 = 0,

10y – 10 = 0.

Отсюда y = 1, x = 5, O(5, 1).

Радиус равен расстоянию от О до любой из вершин треугольника. Находим:

R =½½= = .

Значит уравнение окружности:

(x – 5)² + (y –1)² = 65.

2.В прямоугольном треугольнике ABC известныуравнение одного из катетов 3x – 2y + 5 = 0, координаты вершины C(–5,–5) и координаты середины O(–3/2,–3) гипотенузы AB. Найти координаты

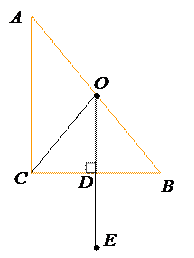вершин A, B и координаты точки E, симметричной O относительно стороны BC. Найти координаты точки пересечения медиан треугольника ABC .

Решение. Пусть катет, уравнение которого нам дано, – это СВ. Он задан общим уравнением вида

ax + by + c = 0.

В данном уравнении геометрический смысл

коэффициентов a и b – это координаты вектора нормали (a, b). Поэтому (3,-2)^ВС.

Составим уравнение перпендикуляра l = ODк стороне СВ и найдем координаты точки D. Вектор будет параллелен OD, т.е. он является направляющим вектором этой прямой. Кроме этого, нам известны координаты точки О на этой прямой. Составляем параметрическое уравнение l :

x = – + 3t, (*)

y = – 3 - 2t .

Имеем D = l I BC. Поэтому, для того, чтобы найти координаты этой точки мы должны решить совместно уравнения l и BC. Подставляем x и y из уравнения l в уравнение BC :

3(– + 3t) –2(–3 -2t)+5 = 0,

– + 9t +6 +4t+5 = 0,

13t = –, t_D= –.

Подставляем найденное t в уравнение l и находим координаты точки D(–3,–2). Для того, чтобы найти координаты E вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это О, вектор скорости – это . Отрезок ОE вдвое длиннее отрезка ОD. Если за время t_D= – мы прошли путь от О до D, то путь от О до E мы пройдем за время t_E= 2t_D= –1. Подставляя это значение в (*), находим E(– 4,5;–1).