Декартова система координат (ДСК) на плоскости. Федеральное государственное образовательное учреждение высшего профессионального образования

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

Федеральное государственное образовательное учреждение высшего профессионального образования

"Мурманский государственный технический университет"

Кафедра высшей математики

и программного обеспечения ЭВМ

Аналитическая геометрия на плоскости. Элементы линейной алгебры. Аналитическая геометрия в пространстве

Часть 1

Методические рекомендации к выполнению контрольных
работ по дисциплине "Математика"
для студентов I курса вечерне-заочного факультета

Мурманск

УДК 514.2 + 512.64 + 514.144.2 (075.8)

ББК 22.151.5 + 22.143 Я73

М 33

Составители: Л.Г. Мостовская, доцент кафедры высшей математики
и программного обеспечения ЭВМ Мурманского государственного технического университета;

Е.Е. Великая, ст. преподаватель той же кафедры

Методические рекомендации рассмотрены и одобрены кафедрой
15 февраля 2006 г., протокол № 4

Рецензент - В.С. Кацуба, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Оригинал-макет подготовлен в авторской редакции

Электронная верстка Т.В. Бекреневой

Oacute; Мурманский государственный

Технический университет, 2007

Оглавление

Введение.. 4

Методические указания к изучению тем "Аналитическая геометрия на плоскости" И "Элементы линейной алгебры. Аналитическая геометрия в пространстве". 5

Справочный материал по теме
"Аналитическая геометрия на плоскости". 6

1. Декартова система координат (ДСК) на плоскости. 6

2. Полярная система координат (ПСК) 7

3. Прямая линия на плоскости. 7

4. Кривые второго порядка. 8

Примерный вариант и образец выполнения
контрольной работы № 1. 11

Справочный материал по темам
"Элементы линейной алгебры.
Аналитическая геометрия в пространстве". 19

1. Матрицы.. 19

2. Линейные операции над матрицами. 20

3. Определители. 21

4. Решение системы трех линейных алгебраических уравнений
с тремя неизвестными методом Крамера. 22

5. Решение системы трех линейных алгебраических уравнений
при помощи обратной матрицы.. 23

6. Векторы. Операции над векторами. 24

7. Уравнение плоскости в пространстве. 27

8. Уравнения прямой в пространстве. 27

Примерный вариант и образец выполнения
контрольной работы № 2. 28

Варианты контрольнЫХ работ. 39

Варианты контрольной работы № 1. 39

Варианты контрольной работы № 2. 41

Рекомендуемая литература.. 45

Введение

Основной формой обучения студентов-заочников математике является самостоятельная работа студентов, которая включает изучение теоретического материала, решение типовых задач с проверкой правильности решения, выполнение контрольных работ.

В настоящих рекомендациях содержатся краткие теоретические сведения, рекомендации к выполнению контрольной работы 1 по теме "Аналитическая геометрия на плоскости" и контрольной работы 2 по теме "Элементы линейной алгебры. Аналитическая геометрия в пространстве", список литературы.

В результате изучения указанных тем студенты I курса должны:

• освоить метод координат на плоскости и научиться решать простые геометрические задачи с использованием уравнений прямой и уравнений кривых второго порядка;

• ознакомиться с основами линейной алгебры (действия над матрицами, вычисление определителей), научиться решать системы линейных алгебраических уравнений методом Крамера и с помощью обратной матрицы;

• знать основы векторной алгебры (линейные операции над векторами, скалярное, векторное и смешанное произведения векторов и их приложения);

• освоить метод координат в пространстве, научиться решать задачи
с использованием средств аналитической геометрии.

В предлагаемых методических рекомендациях даны варианты контрольных работ, справочный материал, необходимый для их выполнения,
а также примеры решения контрольных работ.

Методические указания к изучению тем
"Аналитическая геометрия на плоскости"
И "Элементы линейной алгебры.
Аналитическая геометрия в пространстве"

В таблице приведены наименования тем в соответствии с содержанием контрольных работ и необходимая литература. Перед выполнением контрольных работ рекомендуется изучить соответствующий теоретический материал и решить указанные в таблице задачи.

Таблица 1

Номер конт-рольной работы	Номер задачи	Наименования тем	Литература
		Декартовы координаты точек на плоскости. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнения прямой линии на плоскости. Условия параллельности и перпендикулярности прямых на плоскости	[1], гл. III, § 9.1, 9.2, 10.1, 10.2, 10.3; [2], гл. 3, § 1 - 2, 5, 6; [3], ч. 1, гл.I, № 16 - 20, 74, 76, 99, 100, 102, 105, 111 - 114, 119, 121; [4], гл. 3, № 21, 24, 25, 29, 39, 86 - 88, 91, 94, 95, 122
		Уравнения линий на плоскости в декартовых координатах	[1], гл. III, § 10.1; [2], гл. 3, § 5; [3], ч. 1, гл. I, № 44, 47, 48, 150; [4], гл. 3, № 52, 55, 60 - 67, 136, 148, 159
	3, 4	Кривые второго порядка: окружность, эллипс, гипербола, парабола. Приведение уравнения второго порядка к каноническому виду. Точки пересечения линий на плоскости	[1], гл. III, § 9.3, 11; [2], гл. 3, § 7, 8; [3], ч. 1, гл. I, № 134, 136, 144, 145, 149, 155 - 157, 169, 170, 187 - 195; [4], гл. 3, № 126, 128, 139, 141, 150 - 152, 156
		Полярные координаты точки на плоскости. Связь между декартовыми и полярными координатами. Уравнения линий на плоскости в полярных координатах	[1], гл. III, § 9.1, 10.1; [2], гл. 3, § 3, 5; [3], ч. 1, гл. I, № 29, 30, 33 - 35, 49 - 51; [4], гл. 3, № 44, 45, 53(5), 54
		Матрицы. Операции над матрицами	[1], гл. I, § 1; [2], гл. 10, § 1; [3], ч. 1, гл. IV, № 399 - 403, 414, 415
		Определители. Обратная матрица. Решение систем линейных алгебраических уравнений по формулам Крамера и с помощью обратной матрицы	[1], гл. I, § 2, 3.1, 3.2, 4.1, 4.3; [2], гл. 10, § 2 - 4; [3], ч. 1, гл. I, № 210, 211, 217, 219, 225 - 227; [4], гл. 7, № 20 - 25, 38 - 43

Окончание табл. 1

Номер конт-рольной работы	Номер задачи	Наименования тем	Литература
		Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов	[1], гл. II, § 5 - 8; [2], гл. 9, § 1 - 4, 6 - 8; [3], ч. 1, гл. II, № 244, 248, 256 - 266, 284; [4], гл. 10, № 37, 47, 48, 51, 72, 73, 77, 83 - 84
		Плоскость и прямая линия в пространстве	[1], гл. IV, § 12.1 - 12.6; [2], гл. 9, § 11 - 13; [3], ч. 1, гл. III, № 288, 289, 302, 307, 314, 325, 333, 334, 341; [4], гл. 10, № 104, 113, 119, 131, 132, 141, 151, 153

Примечание. Ссылки на литературу в таблице даны в соответствии
с номерами в списке рекомендуемой литературы.

Справочный материал по теме
"Аналитическая геометрия на плоскости"

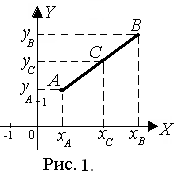
Декартова система координат (ДСК) на плоскости

Расстояние |АВ| между двумя точками А(х_А; у_А) и В(х_В; у_В) (рис. 1):

|AB| = 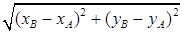. (1)

Деление отрезка в заданном отношении. Если точка С делит отрезок АВ в отношении λ, начиная от точки A (рис. 1),

т. е. 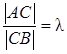, то координаты точки C:

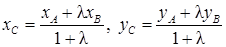. (2)

Если точка С делит отрезок АВ пополам,
т.е. 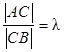=1, то координаты точки C:

. (3)

В ДСК уравнение линии имеет вид F(х, у) = 0 или у = f(х).