Задание. Используется Comsol 3.5, модуль Convection and Diffusion

Используется Comsol 3.5, модуль Convection and Diffusion.

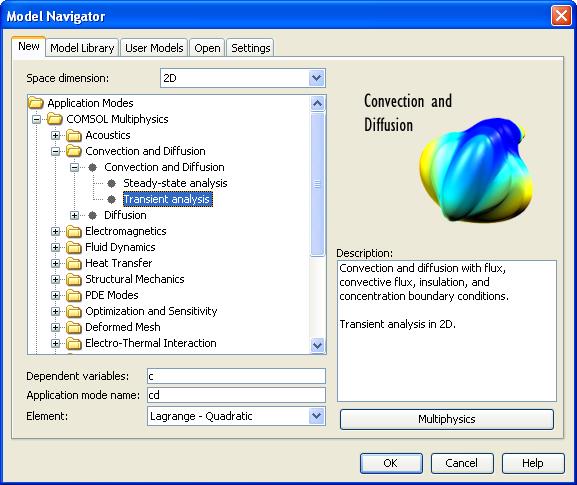
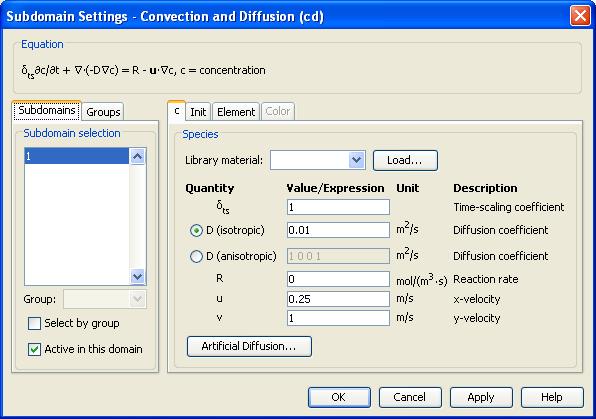
Рис. Настройки объемного домена.

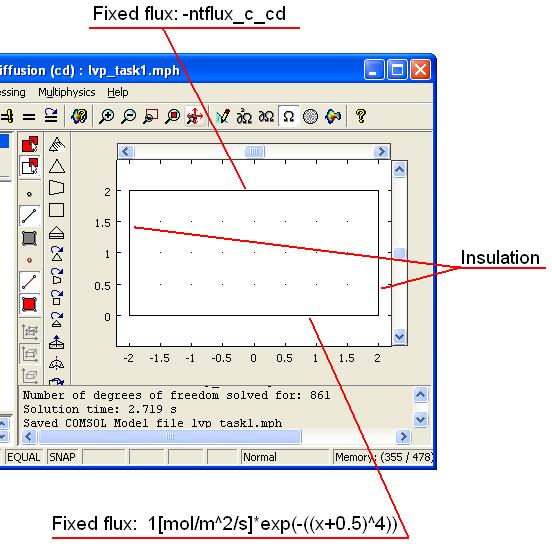
Рис. Граничные условия

	Тип элементов	Степень элементов
Мохова	квадратный неупорядоченный	квадратичный
Красильников Криворуко	треугольный неупорядоченный	квадратичный
Козуб Тейницкий	треугольный неупорядоченный	линейный
Келадзе	квадратный упорядоченный	квадратичный
Дмитриева Лелеков	квадратный упорядоченный	линейный

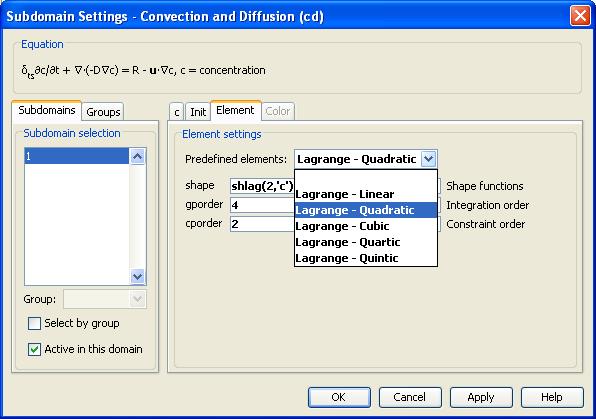
Рис. Выбор степени элементов (линейный или квадратичный).

Что необходимо получить:

В данной задаче определить, при каком размере элемента возникают отрицательные значения концентраций перед фронтом. Для этого после решения построить линейные графики концентрации на оси Y (т.е. на линии x=0). Считать решение устойчивым, если в момент времени t=0,1 на оси симметрии нет отрицательных значений концентрации c. С точностью в 10% определить критическое значение числа Пекле Pe, при котором начинают возникать отрицательные концентрации (Pe=Vh/D). Указать количество степеней свободы в задаче с критическим значением числа Пекле (в меню: Mesh->Mesh statistics->Number of degrees of freedom).

Построить линейные графики концентрации на оси симметрии в разные моменты времени при значении числа Пекле больше критического и меньше критического.

Построить контурные графики концентрации в момент времени t=1 при значении числа Пекле больше критического и меньше критического.