Определение теоретического значения коэффициента Пуассона

Из молекулярно - кинетической теории известно, что внутренняя энергия одного мо­ля равна

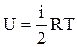
где i - число степеней свободы данного газа. Число степеней свободы определяет число независимых координат, полностью описывающих положение молекулы газа в пространстве. Для идеального одноатомного газа необходимы три координаты, опи­сывающие поступательное движение такой молекулы в пространстве. Следовательно ему приписывают три степени свободы.

Молекула двухатомного идеального газа рассматривается как совокупность двух материальных точек-атомов, жестко связанных недеформируемой связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две сте­пени свободы вращательного движения. Таким образом, двухатомный идеальный газ обладает пятью степенями свободы. Трехатомные и многоатомные нелинейные моле­кулы имеют шесть степеней свободы: три поступательных и три вращательных. Есте­ственно, что жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.

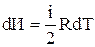подставляя это выражение в (4)

получим

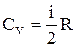(10)

С учетом (10) выражение (7) примет вид

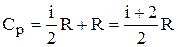(11)

С учетом (10) и (11) получим теоретическое значение коэффициента Пуассона

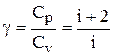(12)

II. Теория метода и описание установки

Величину γ можно определить с помощью установки (рис.1),

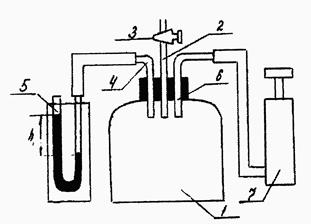состоящей из стеклянного баллона 1,герметично зарытого пробкой, через пробку в баллон пропущена трубка 2, на верхнем конце которой имеется кран 3, соединяющий полость баллона с атмосферой. Через трубку 4, пропущенную через пробку в баллон, полость баллона соединяется с V-образным манометром 5. Через трубку 6 полость баллона соединяется с насосом 7.

Рис.1

В баллон при закрытом кране накачивается воздух. Давление воздуха в баллоне повысится и станет равным

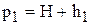
где h₁ - избыток давления воздуха в баллоне над атмосферным давлением Н. Величи­на h₁ измеряется манометром. Открывают на короткое время кран 3, чтобы давление в баллоне сравнялось с атмосферным (р₂ ⁼ Н ), после чего закрывают кран.

Пусть масса воздуха поcле накачивания насосом в сосуде объемом V равна m. При открывании крана часть воздуха выходит. Обозначим массу вышедшего воздуха через Δm, тогда масса оставшегося воздуха

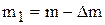
Масса воздуха m₁, которая заключается в объеме V, занимала перед открытием крана меньший объем Vi. Так как процесс кратковременный и заметного теплообмена между газом и стенками баллона нет, то его можно считать адиабатическим. Соглас­но уравнению Пуассона (для массы газа равной m₁) получим

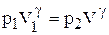(13)

Вследствие адиабатического расширения температура газа понизилась, а затем в результате теплообмена, температура его через небольшой промежуток времени станет равной комнатной. При этом давление газа поднимается до величины

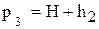
Начальное и конечное состояние газа наблюдается при одинаковой температу­ре. Поэтому на основании закона Бойля-Мариотта получим

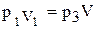(14)

Решая уравнения (13) и (14) относительно у, получим

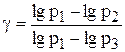(15)

Разложим lg p₁ или lg p₃ в ряд Тейлора, ограничившись в этом случае двумя первыми членами:

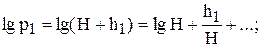
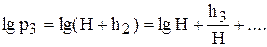
Подставляя эти значения в формулу (15), получим окончательно

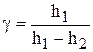. (16)

III. Порядок выполнения работы и обработки

результатов измерений

1. Кран ставят так, чтобы полость насоса соединялась с баллоном.

2. Дейст­вуя насосом осторожно, нагнетают воздух в сосуд до тех пор, пока разность уровней воды в манометре достигнет 200-250 мм.

3. При накачивании воздух, сжимаемый под поршнем насоса нагревается, следовательно, необходимо выждать 2-3 мин. пока, благодаря теплообмену температура в баллоне не станет равной комнатной

4. После этого производят первый отсчет разности уровней в манометре h₁; (в мм водяного столба).

5. Открывают кран, и в тот момент, когда уровни жидкости в обоих коленах манометра сравняются, быстро закрывают кран.

6. Выждав 2-3 мин., пока газ, охлаж­денный при адиабатическом расширении, нагреется до комнатной температуры, производят второй отсчет разности уровней в манометре h₂.

_7. Опыт следует повторить не менее пяти раз, изменяя в каждом случае ве личину h_1.

8. Для каждой пары значений h₁ и h₂ по формуле (16) вычисляют величину γ коэффициента Пуассона.

9. Найти среднее арифметическое значение результатов измерений γ.

10. Вычислить теоретическое значение γ_теор. по формуле (12), считать i==5. т.к. воздух более чем на 99% состоит из двухатомных молекул.

11. Найти относительную погрешность измерений коэффициента Пуассона у по формуле

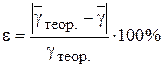
12. Вычислить абсолютную погрешность .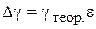

13. Результаты измерений и вычислений записать в таблицу 1.

Таблицу 1

№ опыта	h1, мм	h2, мм	γ		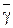γ теор.		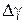Ε,%

14. Записать окончательный результат в виде

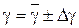
Контрольные вопросы

1. Уравнение состояния идеального газа.

2. Первое начало термодинамики, его применение к основным изопроцессам иде­ального газа.

3. Удельная и молярная теплоемкости, их связь между собой.

4. Уравнение Майера.

5. Коэффициент Пуассона, как он выражается через теплоемкости С_p и С_v, а также через число степеней свободы.

Литература

1. Трофимова, Т.И.. Курс физики [Текст]: учеб.пособ./Т.И.Трофимова.- М: Академия, 2004.- 560с.

2. Савельев, И.В. Курс общей физики [Текст]: в 5-ти кн.: учеб.пособ. / И.В. Савельев.- М.: Астрель: АСМ, 2005. кн.3:Термодинамика и молекулярная физика – 208 с.