Теория метода и описание установки. Адиабатическим называется процесс изменения объёма газа,проходящий без теплообмена с окружающей средой

Адиабатическим называется процесс изменения объёма газа,проходящий без теплообмена с окружающей средой. При адиабатическом процессе изменяются все три параметра, определяющие состояние газа.

Как известно, изменение объёма V связано с изменением давления p. В случае адиабатического процесса эта зависимость выражается уравнением Пуассона

PV g = const.

(3.1)

Показатель адиабаты g является важной термодинамической величиной, характеристикой газа. Он равен отношению теплоёмкости газа при постоянном давлении C_p к теплоёмкости этого же газа при постоянном объёме C_V, то есть

.

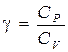(3.2)

Теплоёмкостью называется количество теплоты, необходимое для нагревания тела или системы на один градус:

.

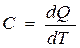(3.3)

Величина теплоёмкости газа зависит от условий, при которых происходит его нагревание. По первому закону термодинамики полученное системой количество теплоты

dQ = dU + dA,

(3.4)

где dU – приращение внутренней энергии термодинамической системы; dA – работа, совершённая системой против внешних сил. Уравнение 1-го закона термодинамики (3.4) записано здесь для бесконечно малых величин.

Внутренняя энергия газов при давлениях порядка атмосферного (» 10⁵ Па) прямо пропорциональна абсолютной температуре газа и числу i степеней свободы молекул газа:

,

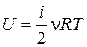(3.5)

где n – количество газа (число молей).

Газ совершает работу только при изменении объёма:

dA = рdV,

(3.6)

поэтому, если нагревать газ при постоянном объёме, то всё тепло, сообщаемое газу извне, полностью идёт на увеличение внутренней энергии. Если же нагревать газ при постоянном давлении, то газ расширяется, при этом сообщаемое газу тепло идёт не только на увеличение внутренней энергии, но и на совершение работы изобарического расширения. Поэтому теплоёмкость газов при p = const больше, чем при V = const. Для идеального газа справедливо следующее соотношение между молярными теплоёмкостями:

,

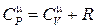(3.7)

причём теплоёмкость прямо пропорциональна числу степеней свободы молекул газа и не зависит от температуры:

,

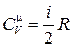(3.8)

где R = 8,31 Дж/(моль×К) – универсальная газовая постоянная.

В случае адиабатного процесса dQ = 0, и, как следует из первого закона термодинамики (3.4), работа газа совершается за счёт изменения его внутренней энергии:

dA = – dU.

(3.9)

При расширении газ совершает положительную работу, следовательно, внутренняя энергия газа уменьшается, и, в соответствии с (3.5), уменьшается температура газа. При адиабатическом сжатии наоборот: работа газа отрицательна, а приращение внутренней энергии положительно. Поэтому при адиабатическом сжатии температура газа увеличивается.

Показатель адиабаты можно определить экспериментально, если осуществить ряд газовых процессов в воздухе, заключённом в сосуде. Очевидно, как следует из выражений (3.2), (3.7) и (3.8), по измеренному значению g можно также найти число i степеней свободы молекул газа. Соответствующую формулу для вычисления i по экспериментально определённому значению g нужно вывести при подготовке к лабораторной работе.

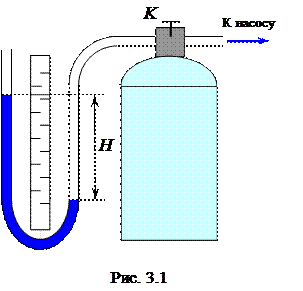Применяемый в данной работе прибор Клемана – Дезорма схематически изображён на рис. 3.1. Он представляет собой стеклянный баллон, плотно закрытый пробкой, через которую пропущены трубки. Одна из трубок имеет кран K, позволяющий устанавливать и прерывать сообщение баллона с атмосферой. Другая трубка соединена с водяным U-образным манометром с одной стороны и с ручным воздушным насосом с другой. Нагнетая насосом воздух в баллон и быстро выпуская его, можно осуществить процесс, близкий к адиабатическому.

Теперь перейдём непосредственно к описанию методики определения показателя адиабаты. Известно, что любое состояние газа характеризуется определёнными значениями параметров р, V и T. Процесс – это переход из одного состояния в другое, т.е. изменение параметров. В координатах р, V состояние газа изображается точкой, а газовый процесс – линией. На рис. 3.2 представлены два процесса: адиабатический 1®2, и изохорный 2®3. Покажем, что показатель адиабаты g можно определить, осуществив три состояния газа и записав последовательно уравнения процессов.

1. Газ в состоянии 1, полученном после нагнетания воздуха в сосуд и установления комнатнойтемпературы T₁, имеет параметры: р₁ = р_ат + H, где H – избыточное давление в сосуде над атмосферным давлением р_ат; V₁ – объём единицы массы воздуха в сосуде. На графике этому состоянию соответствует точка 1.

Примечание. Здесь все давления выражаются в метрах водяного столба. Фактически избыточное давление равно rgH, где r – плотность воды. Поскольку в дальнейшем мы придём к отношению давлений, то множитель rg сократится.

2. Если теперь на короткое время соединить сосуд с атмосферой, открыв кран K (см. рис. 3.1), то воздух в баллоне расширится и перейдёт в состояние 2 с давлением р₂ = р_ат. Единица массы газа займёт объём V₂ > V₁, температура понизится до некоторого значения T₂ < T₁ (рис. 3.2, точка 2). Переход газа из состояния 1 в состояние 2 можно считать адиабатическим процессом, поскольку за время расширения газ в сосуде не успевает обменяться теплом с окружающей средой.

Для адиабатического перехода из состояния 1 в состояние 2 справедливо уравнение Пуассона (3.1):

.

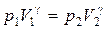(3.10)

3. Воздух, оставшийся в сосуде, сохраняя объём постоянным (V₃ = V₂), постепенно нагревается до комнатной температуры (T₃ = T₁), и давление повышается до значения р₃ = р_ат + h (точка 3 на рис. 3.2).

Газ в состояниях 3 и 1 имеет одну и ту же комнатную температуру. Значит, эти состояния можно связать уравнением Бойля – Мариотта:

р1V1 = р3V3.

(3.11)

Из уравнений (3.10) и (3.11) легко получить связь между начальным давлением р₁ и конечным давлением р₃

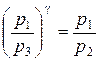(3.12)

и, логарифмируя последнее равенство, определить показатель степени

.

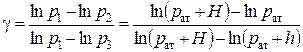(3.13)

Учитывая, что H и h много меньше р_ат (давление атмосферы соответствует 10 м водяного столба, а H не превышает 300 мм), и используя формулу приближённых вычислений: ln(1+x) » x (при x << 1), можно получить расчётную формулу для показателя адиабаты:

.

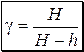(3.14)

Эта формула даёт правильный результат, если процесс расширения 1®2 действительно адиабатический, и за время расширения теплота не проникает сквозь стенки сосуда. Практически это условие можно выполнить, если провести расширение очень быстро. Однако здесь возникает другая проблема – процесс становится существенно неравновесным, так как температура и давление не успевают выравниваться в объёме сосуда, и применять уравнения (3.10) и (3.11) не совсем корректно.

Анализ ситуации с теплообменом показывает: чем дольше длится процесс расширения газа, тем большее количество теплоты проникает из комнаты в сосуд, и тем меньше будет понижение температуры при переходе газа в сосуде из состояния 1 в состояние 2 (см. рис. 3.2). Поэтому при последующем изохорном нагревании (процесс 2®3) давление поднимется на меньшую величину h', чем при адиабатическом процессе: h' < h, и рассчитанное по формуле (3.14) значение g будет заведомо меньше теоретического. При t ® ¥ процесс расширения становится изотермическим, h' ® 0, а показатель g ®1. С увеличением времени t, в течение которого сосуд сообщается с атмосферой, значение h' уменьшается по экспоненциальному закону:

h' = h0e–at.

(3.15)

Здесь h₀ – значение величины h в уравнении (3.14), которое получилось бы при мгновенном переходе из состояния 1 в состояние 2, когда dQ действительно равно нулю. После логарифмирования получим линейную зависимость

lnh' = lnh0– at,

(3.16)

где a – коэффициент, зависящий от параметров лабораторной установки. Проведя измерения h' при разных t, можно построить график зависимости lnh'(t) (рис. 3.3), и определить по нему lnh₀, продолжая линию графика до пересечения с осью ординат (см. рис 3.3). Затем по логарифму найти h₀, и вычислить показатель g₀ по формуле (3.14).

Задание 1. Определение показателя адиабаты атмосферного воздуха

С учётом теплообмена

В этом случае, чтобы использовать уравнение (3.16) и график на рис. 3.3, нужно обеспечить одинаковые начальные условия: давление р₁ и температуру Т₁. Будем считать, что второе условие заведомо выполняется, а для выполнения первого условия следует накачивать воздух в баллон до одного и того же значения H. Достаточно приемлемые результаты получаются, если производить накачивание каждый раз с атмосферного давления, в медленном темпе, с одинаковым числом качков насоса.

1. Откройте кран K (см. рис. 3.1) и, выждав около минуты, закройте его.

2. Создайте в баллоне избыточное давление, накачивая воздух в баллон. Следите при этом за показаниями манометра и считайте число качков.

3. Дождитесь, пока температура в сосуде не сравняется с температурой в лаборатории. Определите по манометру величину H₀ и запишите в табл. 3.1.

4. Откройте кран K одновременно с включением секундомера и через время t₁ быстро закройте его. Значение времени t₁ задаёт преподаватель. Его нужно записать в табл. 3.1 числом (например, 4,0 с вместо t₁)

5. Выждите, пока давление в баллоне не стабилизируется, определите по манометру величину h', запишите в табл. 3.1 в столбец с t = t₁.

Таблица 3.1

Параметры	Время расширения, с
t1	t2	t3	t4	t5
h'						h0 =
lnh'						lnh0 =
H0 » const						áH0ñ =

6. Проведите аналогичные измерения по пп. 1–5, оставляя кран открытым в течение времени t_n = nt₁, где п = 2, 3, 4, 5. Значения t_n, h', H₀ записывайте в табл. 3.1. Последний столбец таблицы заполняется после расчётов и построения графика (см. рис. 3.3)