Тема: Множества и их спецификация.
Практическая работа №1.
Задание №1.
Даны множества:
А = {–1; 0; 1},
В = [–2; 0) – полуинтервал на числовой оси,
С = [–0.5; 2] - отрезок на числовой оси.
Найти:
АÈВ, АÈВÈС, АÇВ, ВÇС, АÇВÇС, A \ B, B \ A, A \ C, C \ A, (А \ В) \ С, А \ (В \ С), А Å B, A Å B Å C.
Изобразить на плоскости: А ´ В, А ´ С, В ´ С. Найти 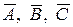 , считая универсальным множеством множество всех вещественных чисел.
, считая универсальным множеством множество всех вещественных чисел.
Решение:
Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:
АÈВ = {[–2; 0]; 1}
АÈВÈС = [–2; 2]
Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:
АÇВ = {–1}
ВÇС = [–0.5; 0)
АÇВÇС = Æ – пустое множество
Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому
А \ В = {0; 1}
В \ А = {[–2; –1); (–1; 0)}
А \ С = {–1}
С \ А = {[–0.5; 0); (0; 1); (1; 2]}
(A \ B) \ C = Æ
A \ (B \ C) = {0; 1}
Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, а абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:
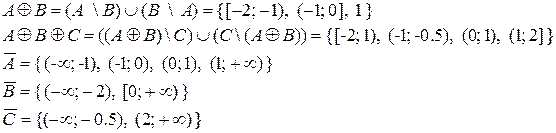

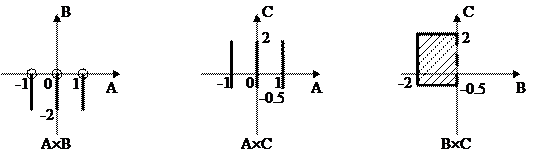 Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что
Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что 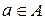 и
и 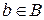 , поэтому:
, поэтому:
Задание№2
Для заданного семейства множеств 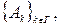 где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е.
где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е. 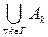 и
и 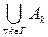 (по всем возможным индексам
(по всем возможным индексам 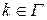 ).
).
{Ak}kÎℝ, где для всякого вещественного индекса k множество
Аk={ (x, y): |x|+|y| ≤ |γ| и x, yÎℝ }.
Решение: рассмотрим множества Аk для некоторых фиксированных индексов k.
При k=0 множество А0={ (x, y): |x|+|y| ≤ 0}={(0;0)} – центр вещественной плоскости.
При k=0.5 и k= –0.5 А0.5=А‑0.5={ (x, y): |x|+|y| ≤ 0.5} – ромб в центре вещественной плоскости с диагоналями, равными 1 и направленными вдоль осей координат.
При k=2 и k= –2 А2=А‑2={ (x, y): |x|+|y| ≤ 2} – ромб с диагоналями, равными 4 и т. д..
При увеличении абсолютной величины индекса k диагонали ромба, расположенного в центре вещественной плоскости, увеличиваются и при |k|→+ 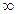 ромб А
ромб А 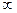 занимает всю вещественную плоскость. Таким образом, объединение по всем вещественным индексам k равно
занимает всю вещественную плоскость. Таким образом, объединение по всем вещественным индексам k равно 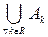 = ℝ ´ ℝ = ℝ2 – вся вещественная плоскость, а пересечение по всем вещественным индексам k равно
= ℝ ´ ℝ = ℝ2 – вся вещественная плоскость, а пересечение по всем вещественным индексам k равно 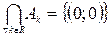 – центр вещественной плоскости.
– центр вещественной плоскости.
Задание№3
Докажите тождество, используя только определения операций над множествами: 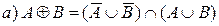
Решение: (1) Пусть 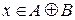 , тогда
, тогда 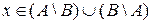 . Отсюда следует, что 1)
. Отсюда следует, что 1) 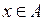 и
и 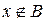 или 2)
или 2) 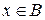 и
и 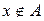 . В первом случае из того, что
. В первом случае из того, что 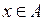 следует, что х принадлежит также объединению множества А с любым другим множеством, в том числе и множеством В, т.е.
следует, что х принадлежит также объединению множества А с любым другим множеством, в том числе и множеством В, т.е. 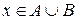 . Но в то же время
. Но в то же время 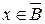 и, следовательно, х принадлежит также объединению
и, следовательно, х принадлежит также объединению 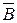 с любым другим множеством, в том числе и множеством
с любым другим множеством, в том числе и множеством 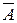 , т.е.
, т.е. 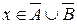 . Таким образом,
. Таким образом, 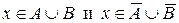 , т.е.
, т.е. 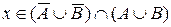 . Аналогично во втором случае: из того, что
. Аналогично во втором случае: из того, что 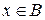 следует, что х принадлежит также и
следует, что х принадлежит также и 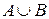 . И в то же время, поскольку
. И в то же время, поскольку 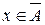 , то х принадлежит также объединению
, то х принадлежит также объединению 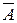 , с любым другим множеством, в том числе и множеством
, с любым другим множеством, в том числе и множеством 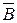 , т.е.
, т.е. 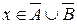 . И также как в первом случае имеем:
. И также как в первом случае имеем: 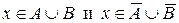 , тем самым
, тем самым 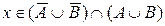 .
.
(2) Пусть теперь 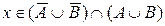 . Тогда
. Тогда 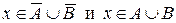 , отсюда
, отсюда 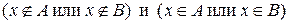 . Следовательно, если
. Следовательно, если 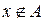 , то
, то 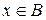 , т.е.
, т.е. 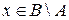 . Если же
. Если же 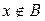 , то
, то 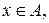 и значит
и значит 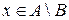 . Таким образом,
. Таким образом, 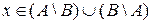 , что равносильно тому, что
, что равносильно тому, что 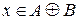 . Из (1) и (2) следует справедливость тождества.
. Из (1) и (2) следует справедливость тождества.
Задание№4
Докажите тождество, используя диаграммы Эйлера-Венна.
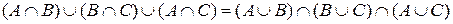
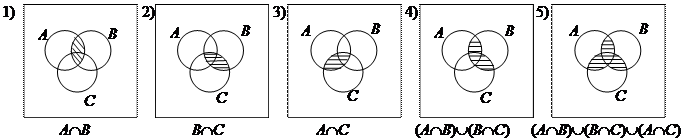
Решение: Изобразим диаграмму для левой части тождества по шагам:
Теперь диаграмму правой части по шагам:
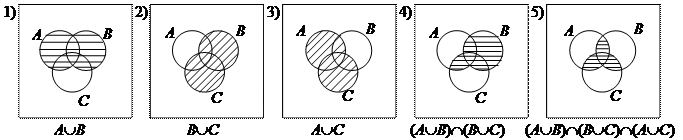
Ввиду того, что заштрихованные области, полученные на последнем шаге для левой и правой части тождества, одинаковы, можно заключить, что исходное выражение верно.
Задания для самостоятельного решения:
Задание №1
Для заданных множеств А, В и С найдите:
АÈВ, АÈС, ВÈС, АÈВÈС, АÇВ, АÇС, ВÇС, АÇВÇС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразите на плоскости А´В, А´С, В´С. Найдите 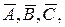 считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
Задание №2
Для заданного семейства множеств 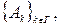 где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е.
где Г – заданное индексное множество, найдите объединение и пересечение всех множеств семейства, т.е. 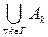 и
и 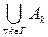 (по всем возможным индексам
(по всем возможным индексам 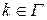 ).
).
Задание №3
Докажите тождества, используя только определения операций над множествами.
Задание №4
Докажите тождество, используя диаграммы Эйлера – Венна.
Варианты заданий:
Вариант№1
1. А = (0; 2] – полуинтервал на числовой оси
В = [1; 5] – отрезок числовой оси
С = (–1; 2) – интервал на числовой оси
2. 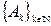 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
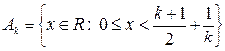
3. 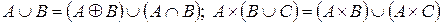
4. . (А \ В) 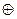 (В \ С)
(В \ С) 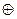 (В \ А)
(В \ А) 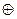 (С \ В) = А
(С \ В) = А 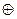 С
С
Вариант№2
1. А = {0, 1, 2, 3}– четырехэлементное множество
В = [–3; 3] – отрезок числовой оси
С = (-2; 2) – интервал на числовой оси
2. 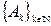 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
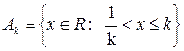
3. 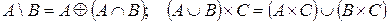
4. (А \ В) 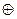 (В \ С)
(В \ С) 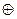 (С \ А) = (В \ А)
(С \ А) = (В \ А) 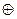 (С \ В)
(С \ В) 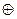 (А \ С)
(А \ С)
Вариант №3
1. А = (–1; +∞)– интервал на числовой оси
В = (–∞; 10] – полуинтервал на числовой оси
С = [–5; +15] – отрезок числовой оси
2. 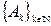 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
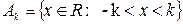
3. 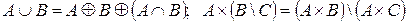
4. (А 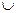 В)
В) 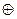 (С
(С 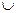 D) = В
D) = В 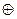 С, если А
С, если А 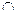 В = D и C
В = D и C 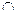 D = A
D = A
Вариант №4
1. А = (–∞; 2]– полуинтервал на числовой оси
В = [–3; 3] – отрезок числовой оси
С = (0; 4) – интервал на числовой оси
2. 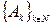 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
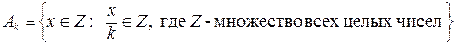
3. 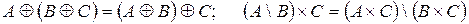
4. 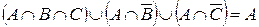
Вариант №5
1. А = (–2; 3) – интервал на числовой оси
В = [0; 4] – отрезок числовой оси
С = {2; 3} – двухэлементное множество
2. 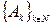 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
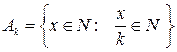
3. 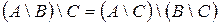
Если 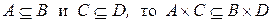
4. 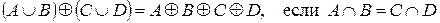
Вариант №6
1. А = [–5; 4]– отрезок числовой оси
В = (-∞; ∞)– интервал на числовой оси
С = (–1; 0] – полуинтервал на числовой оси
2. 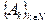 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
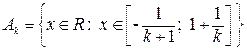
3. 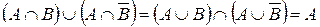
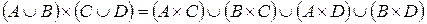
4. 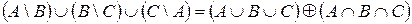
Вариант №7
1. А = (2; 5]– полуинтервал на числовой оси
В = (0; 1)– интервал на числовой оси
С = {–2; -1; 0} – трехэлементное множество
2. 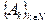 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
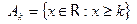
3. 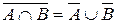
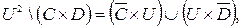 где U – универсальное множество
где U – универсальное множество
4. 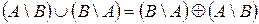
Вариант №8
1. А = (–1; 1)– интервал на числовой оси
В = [1; 2] – отрезок числовой оси
С = (–∞; 1] - полуинтервал на числовой оси
2. 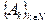 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
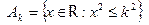
3. 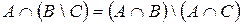
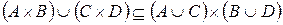
4. 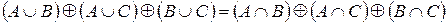
Вариант №9
1. А = (5; 15] – полуинтервал на числовой оси
В = [5; 10] – отрезок числовой оси
С = {4; 5; 6} – трехэлементное множество
2. 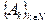 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
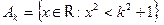
3. 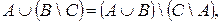 если
если 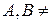 Æ
Æ
если 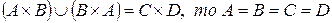
4. 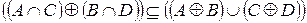
Вариант №10
1. А = (0; 3) – интервал на числовой оси
В = [–1; 3] – отрезок числовой оси
С = (–1; 0] - полуинтервал на числовой оси
2. 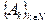 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
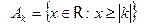
3. 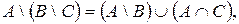
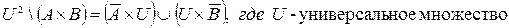
4. 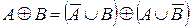
Вариант №11
1. А = [–5; 2) – полуинтервал на числовой оси
В = [–5; 5] – отрезок числовой оси
С = (–1; 1) - интервал на числовой оси
2. 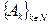 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
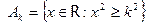
3. 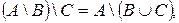
Если 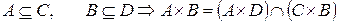
4. 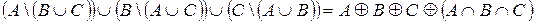
Вариант №12
1. А = (0; 5) – интервал на числовой оси
В = {-2, 0; 1; 2} – четырехэлементное множество
С = [–1; 1] - отрезок числовой оси
2. 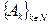 , где ℕ – множество всех натуральных чисел и " kÎℕ
, где ℕ – множество всех натуральных чисел и " kÎℕ
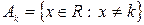
3. 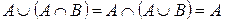
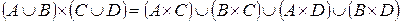
4. 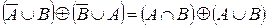
Вариант №13
1. А = (–∞; ∞) – интервал на числовой оси
В = [0; +∞) – полуинтервал на числовой оси
С = (–∞; 5) - интервал на числовой оси
2. 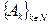 , где ℕ– множество всех натуральных чисел и " kÎℕ
, где ℕ– множество всех натуральных чисел и " kÎℕ
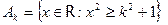
3. 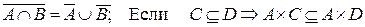
4. 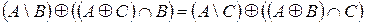
Вариант №14
1. А=[– 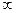 ; 3) – полуинтервал на числовой оси
; 3) – полуинтервал на числовой оси
В=[3; 10] – отрезок числовой оси
С=(3; + 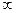 ) – интервал на числовой оси
) – интервал на числовой оси
2. {Аk}kÎℝ, где ℝ – множество всех вещественных чисел и 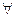 k
k 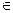 ℝ
ℝ
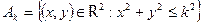
3. (A ÇB) \ C=(A \ C)Ç (B \ C)
(A ´ B) È (C ´ D) Í (A È C) ´ (B È D)
4. (A Å (A \ B)) Ç 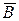 = Æ
= Æ
Вариант № 15
1. А=[–11; 1] –отрезок числовой оси
В=[–1; 3) – полуинтервал на числовой оси
С=(-2; 2) – интервал на числовой оси
2. {Аk}k 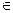 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 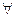 k Îℝ
k Îℝ
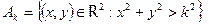
3. A \ (B Ç C) = (A \ B) È (A \ C); (A \ B) ´ C = (A ´ C) \ (B ´ C)
4. ((A È C) Å (B È D)) 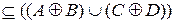
Вариант №16
1. А = (–0; 1) –интервал на числовой оси
В = {–1; 0; 1} – трехэлементное множество
С = [5; 10] – отрезок числовой оси
2. {Аk}k 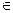 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 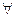 k Î ℝ
k Î ℝ
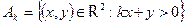
3. 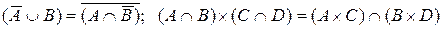
4. 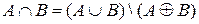
Вариант №17
1. А=(-1; 0] – полуинтервал на числовой оси
В=(0; 1) – интервал на числовой оси
С={-5;- 1; 1} – трехэлементное множество
2. {Аk}k 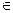 ℝ, где ℝ – множество всех вещественных чисел и
ℝ, где ℝ – множество всех вещественных чисел и 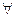 k Îℝ
k Îℝ
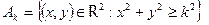
3. 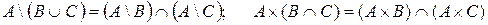
4. 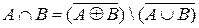
Вариант №18
1. А= {–1; 0; 1} – трехэлементное множество
В=(–1; 0.5) – интервал на числовой оси
С=[0; 1] – отрезок числовой оси
2. {Аk}kÎℝ, где ℝ – множество всех вещественных чисел и 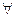 k Îℝ
k Îℝ
Ak = {xÎℝ : x2 ≥ k2 + 1 }
3. 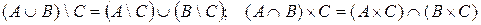
4. 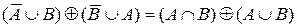
Вариант №19
1. А= [–6; +6) – полуинтервал на числовой оси
В=[–10; 2] –отрезок на числовой оси
С={-1} – одноэлементное множнство
2. {Аk}kÎℝ, где ℝ – множество всех вещественных чисел и 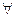 k Îℝ
k Îℝ
Ak = {x 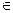 ℝ: x2 +1< k2 }
ℝ: x2 +1< k2 }
3. 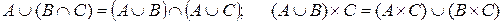
4. 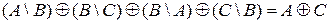
Вариант № 20
1. А= (–1; 4) – интервал на числовой оси
В=[0; 1] – отрезок числовой оси
С=(-2; 0] – полуинтервал на числовой оси
2. {Аk}kÎℝ, где ℝ – множество всех вещественных чисел и " k Îℝ
Ak = { (x, y): |x| + |y| ≥ |k|, где x, y 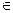 ℝ }
ℝ }
3. 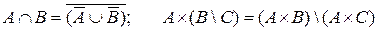
4. 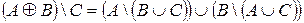
Практическая работа №2
Тема: Функции и отображения.
Задание №1
Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию ƒ ◦ g, g ◦ ƒ, обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A), ƒ –1(B), g-1(B). Найдите также неподвижные точки отображений.
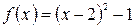 и
и 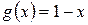 , A = [0; 3] и B = [ ‑1; 0].
, A = [0; 3] и B = [ ‑1; 0].
Решение: область определения отображения f – это множество таких значений х, для которых имеется вещественное число у такое, что у=f(x). И, так как для любого вещественного числа х найдется число у с указанным свойством, то пр1f =ℝ – множество всех вещественных чисел.
Аналогично, область определения отображения g: пр1g =ℝ.
Область значений отображения f – это множество всех образов элементов хÎпр1f. Тем самым, пр2f ={yÎ ℝ.: y ³ -1 }. А область значений отображения g – это множество всех вещественных чисел, т.е. пр2g =ℝ.
Отображение g является инъективным, поскольку для каждого уÎпр2g, имеется ровно один хÎ пр1g (или каждый образ имеет ровно один прообраз). Отображение f инъективным не является, т.к. для некоторых уÎпр2f, имеется более одного прообраза, например: для у=0 прообразами будут х=1 и х=3.
Отображение g является сюрьективным, поскольку для каждого уÎпр2g, имеется хотя бы один хÎпр1g (или каждый образ имеет хотя бы один прообраз). Отображение f также является сюрьективным, т.к. для каждого уÎпр2f, имеется хотя бы один хÎпр1f такой, что у = f(x).
Так как g одновременно инъективно и сюрьективно, то оно является биективным отображением.
Найдем композицию отображений:
(f∘g)(x) = f(g(x)) = (g(x)–2)2–1 = (1–x–2)2 –1 = (–x–1)2 – 1=(x+1)2–1,
(g∘f)(x) = g(f(x)) =1– f(x) = 1 – (x–2)2 +1 = 2 – (x–2)2.
Отображение f обратимо справа, как сюрьекция. И 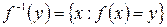 , где y³ –1. Из выражения
, где y³ –1. Из выражения 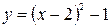 найдем x. Тогда
найдем x. Тогда 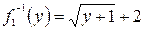 и
и 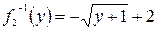 , где y³ –1.
, где y³ –1.
При этом, (f∘f ‑1)(у) = f(f ‑1(y))= 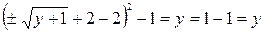 – тождественное отображение при y ³ ‑1.
– тождественное отображение при y ³ ‑1.
Отображение g обратимо как слева, так и справа, как биекция. И 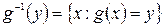 , где y любое. Из выражения
, где y любое. Из выражения 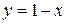 следует:
следует: 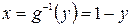 . И при этом: (g∘g‑1 )(у) = g(g‑1(y)) = 1 – ( 1– y ) = y и (g‑1∘g )(х) =
. И при этом: (g∘g‑1 )(у) = g(g‑1(y)) = 1 – ( 1– y ) = y и (g‑1∘g )(х) = 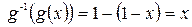 – тождественные отображения.
– тождественные отображения.
По свойствам композиции 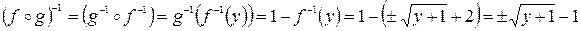
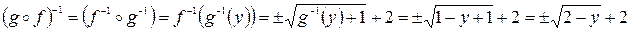
f(A) = { y = f(x), где xÎA }, поэтому f(A)=[–1; 3].
Аналогично, g(A) = { y = g(x), где xÎA } = [–2; 1].
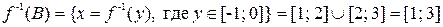
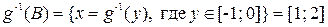
Найдем неподвижные точки. По определению это такие х, что: f(x)=x и g(x)=x. Таким образом, x = (x–2)2–1. Отсюда x2–5x+3=0 и т. к. дискриминант D=25–12=13>0, то 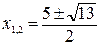 – две неподвижные точки f(x).
– две неподвижные точки f(x).
Из g(x)=x следует, что x=1–x и 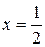 – неподвижная точка g(x).
– неподвижная точка g(x).
Задание №2
Найти композицию соответствий S 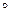 Г и множества B,C, если известно множество А={1,2,3,4}, законы R=2x+3 и G=y2, Г=(G,A,B), S=(R,B,C).
Г и множества B,C, если известно множество А={1,2,3,4}, законы R=2x+3 и G=y2, Г=(G,A,B), S=(R,B,C).
Решение:
По определению композиция это: S∘Г=(R∘G, А, С), в свою очередь, композиция законов это: R∘G={(x,z): $yÎB и (x,y)ÎG и (y,z)ÎR}. Значит, для нахождения композиции графиков нужно в график R вместо переменной x подставить график G: R 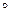 G=2y2+3. Для получения значений элементов множества В, нужно применить закон G к элементам множества А: В={12,22,32,42}={1,4,9,16}. Получение значений элементов множества С возможно двумя способами: первый – применить закон R к элементам множества В: С={2
G=2y2+3. Для получения значений элементов множества В, нужно применить закон G к элементам множества А: В={12,22,32,42}={1,4,9,16}. Получение значений элементов множества С возможно двумя способами: первый – применить закон R к элементам множества В: С={2 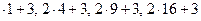 }={5, 11, 21, 35}; второй – применить композицию графиков ко множеству А.: C={
}={5, 11, 21, 35}; второй – применить композицию графиков ко множеству А.: C={ 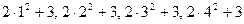 }={5, 11, 21, 35}. Результаты двух способов совпадают. Все компоненты найдены и композиция соответствий будет иметь вид: S
}={5, 11, 21, 35}. Результаты двух способов совпадают. Все компоненты найдены и композиция соответствий будет иметь вид: S 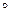 Г=(2y2+3, {1,2,3,4}, {5,11,21,35})
Г=(2y2+3, {1,2,3,4}, {5,11,21,35})
Задания для самостоятельного решения:
Задание №1
Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A), ƒ –1(B), g-1(B). Найдите также неподвижные точки отображений.
Задание №2
Найти композицию соответствий S 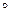 Г и множества B,C.
Г и множества B,C.
Варианты заданий:
Вариант №1
1.
- f=cos(x), g=cos(x)-0.5, A=[-
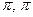 ,], B=(-
,], B=(- 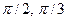 ]
] - f=(x-1)/3, g=y3, A=[-1,2], B=(1,3]
- f=x-3, g=(y+1)2, A=[1,12], B=(-4,0)
2.
- A={-2,-4,2,4}, R=x2-1, G=y+2
- A=
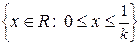 , R=x/2, G=y2/2
, R=x/2, G=y2/2
Вариант №2
1.
- f=sin(x)/2, g=2cos(x), A=[-
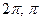 ,], B=(-
,], B=(- 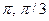 ]
] - f=2(x-1), g=(y+2)/2, A=[1,4], B=[11,0]
- f=x, g=3y2, A=(0,1], B=[-1,1)
2.
- A={0,0.1,0.2,0.3,0.4}, R=0.25x-0.75,G=y2
- A=
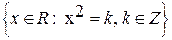 , R=x0.5, G=y2
, R=x0.5, G=y2
Вариант №3
1.
- f=2sin(x), g=1+cos(x), A=[-
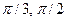 ,], B=(-
,], B=(- 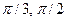 ]
] - f=x, g=(y2+2)/2, A=[-1,1], B=[5,8]
- f=
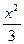 +x, g=y-2, A=[-1,1], B=(-1,1)
+x, g=y-2, A=[-1,1], B=(-1,1)
2.
- A={0,1,2,3,4}, R=x+1, G=(y+1)2
- A=
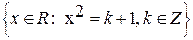 , R=x0.5, G=y2
, R=x0.5, G=y2
Вариант №4
1.
- f=sin(x)/3, g=cos(x/3), A=[-
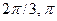 ,], B=[-
,], B=[- 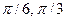 ]
] - f=x3-x, g=1-
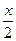 , A=(-1,4), B=[-3,6]
, A=(-1,4), B=[-3,6] - f=2x, g=y2/3, A=(-5,1), B=[0,-1)
2.
- A={1,3,5,7}, R=x-3,G=(y+5)/3
- A=
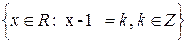 , R=x+1, G=2y2
, R=x+1, G=2y2
Вариант №5
1.
- f=sin(x/2), g=2cos(2x), A=[0,
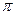 ), B=(-
), B=(- 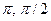 )
) - f=
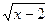 , g=y, A=[-2,4], B=(1,10)
, g=y, A=[-2,4], B=(1,10) - f=-x2, g=1/y2, A=(0,1], B=[-1,1)
2.
- A={-4,-3,-2,-1}, R=(x-1)2,G=y+1
- A=
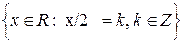 , R=2x G=y2/2
, R=2x G=y2/2
Вариант №6
1.
- f=sin2(x) g=2cos(x), A=[-
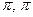 ,], B=(-2
,], B=(-2 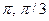 ]
] - f=x2+1, g=(y+2)/(2-y), A=[-2,2], B=[-6,0)
- f=2x/(1-x2), g=y+3, A=[0,1], B=(-2,0)
2.
- A={1/3,1/9,1/12,1/15}, R=3x, G=y2
- A=
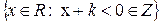 , R=1/(x+2), G=y/(1-y)
, R=1/(x+2), G=y/(1-y)
Вариант №7
1.
- f=sin(x)/2+sin2x, g=cos(x), A=[
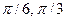 ,], B=(-
,], B=(- 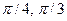 ]
] - f=1-x2/2, g=y+2, A=(0,4), B=[-3,3]
- f=
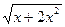 , g=y/3, A=(0,1], B=[-1,1)
, g=y/3, A=(0,1], B=[-1,1)
2.
- A={3,5,9,10}, R=2x, G=1/y;
- A=
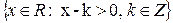 , R=x+4, G=y/(y+1)
, R=x+4, G=y/(y+1)
Вариант №8.
- f=sin(x)/2, g=2cos(x), A=[-
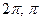 ,], B=(-
,], B=(- 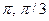 ]
] - f=2(x-1), g=(y+2)/2, A=[1,4], B=[-11,0]
- f=x, g=3y2, A=(0,1], B=[-1,1)
2.
- A={0,0.1,0.2,0.3,0.4}, R=0.25x-0.75,G=y2
- A=
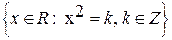 , R=x0.5, G=y2
, R=x0.5, G=y2
Вариант №9
1.
- f=sin(x)-1, g=(2cos(x))/3, A=[-
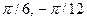 ,], B=(-
,], B=(- 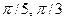 ]
] - f=x+х2, g=5y+2, A=[-3,3], B=[-4,0]
- f=x/3+1, g=(y+1)2, A=(-3,-1), B=(-1,1)
2.
- A={-21, -14, -7, 0, 7, 14, 21}, R=x/7,G=y+7
- A=
 , R=x+1, G=y/2
, R=x+1, G=y/2
Вариант №10
1.
- f=х/2+sin(x), g=cos(x)+cos(x/3), A=[
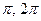 ,], B=(-
,], B=(- 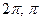 ]
] - f=2x-х/4, g=y+у2, A=(-2,2), B=[1,10]
- f=(x+4)/3, g=y2/2, A=(0,1], B=[1,2)
2.
- A={-1, 1, -2, 2, -3, 3}, R=x, G=y2
- A=
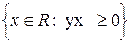 , R=2x, G=3y
, R=2x, G=3y
Вариант №11
1.
- f=sin(x)-2tg(x), g=cos(x)-cos(2)/2, A=[
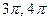 ,], B=(-
,], B=(- 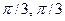 ]
] - f=(3/x)+(x/3), g=y-y2, A=[-3,3], B=[6,9]
- f=2+x, g=3y-1, A=(-2,1), B=(4,1)
2.
- A={0,5,10,15,20}, R=x-5, G=y/5
- A=
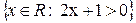 , R=2x, G=y+2
, R=2x, G=y+2
Вариант №12
1.
- f=tg(3x), g=sin(x)+1, A=[-
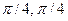 ,], B=(-
,], B=(- 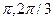 )
) - f=2x-1, g=1/(y+1), A=(0,2), B=[-3,2]
- f=x-4, g=3y/2, A=(1,1], B=(-4,4)
2.
- A={-1,-3,-5,-7,-9}, R=x+1,G=y/2
- A=
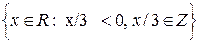 , R=x/3, G=y2
, R=x/3, G=y2
Вариант №13
1.
- f=3sin(x), g=sin(x/3), A=[-
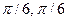 ,], B=(-
,], B=(- 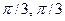 ]
] - f=3/(x-2), g=y2+3, A=[-1,0], B=(2,12)
- f=x3, g=y-7, A=(-8,8], B=[1,7]
2.
- A={-8, 8, 15, 22, 29}, R=x-1,G=y/7
- A=
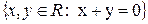 , R=3x-2, G=2y2
, R=3x-2, G=2y2
Вариант №14
1.
- f=cos(x), g=tg(x)-1, A=[-
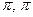 ), B=[
), B=[ 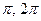 ]
] - f=1/x, g=y+4, A=[3,7], B=[-7,2]
- f=x4, g=2y-2, A=[-10,1], B=[0,5)
2.
- A={5, 3, 6, 4, 2}, R=2x-1,G=y+4
- A=
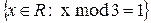 , R=x+2, G=y/3
, R=x+2, G=y/3
Вариант №15
1.
- f=(sin(x))/3, g=3cos(x), A=[-
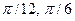 ], B=(
], B=( 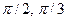 ]
] - f=x2-3, g=(y+2)2, A=[2,5], B=(-3,-1)
- f=6x-1, g=4-y2, A=(-4,4], B=[2,8)
2.
- A={1/3, 1/6, 1/9, 1/12}, R=(3x)2, G=y-3
- A=
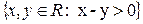 , R=4x, G=y2-2
, R=4x, G=y2-2
Вариант №17
1.
- f=sin(x)/2, g=2cos(x), A=[-
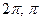 ,], B=(-
,], B=(- 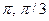 ]
] - f=2(x-1), g=(y+2)/2, A=[1,4], B=[11,0]
- f=x, g=3y2, A=(0,1], B=[-1,1)
2.
- A={0,0.1,0.2,0.3,0.4}, R=0.25x-0.75,G=y2
- A=
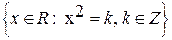 , R=x0.5, G=y2
, R=x0.5, G=y2
Вариант №18
1.
- f=sin(x)+cos(x), g=tg(x)/3, A=[-
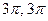 ,], B=(
,], B=( 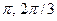 )
) - f=x2, g=
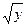 , A=[1,4], B=[3,9]
, A=[1,4], B=[3,9] - f=2+x, g=y2/3, A=[-4,4), B=[-2,2]
2.
- A={1/2, 1/3, 1/4, 1/5}, R=3x, G=y+3
- A=
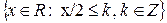 , R=2x, G=y/2
, R=2x, G=y/2
Вариант №19
1.
- f=sin(x), g=2ctg(x), A=[
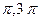 ,], B=(-
,], B=(- 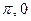 )
) - f=(x/3)+(x/5), g=4y, A=(-1,4], B=[0,9]
- f=x+1, g=y2+4, A=(-6,6], B=[-5,1)
2.
- A={-5, 5, -6, 6, -7, -8, 8}, R=x+4, G=y2
- A=
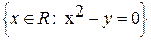 , R=x-5, G=y/3
, R=x-5, G=y/3
Вариант №20
1.
- f=tg(x)/2, g=2cos(x), A=[-
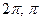 ,], B=(-
,], B=(- 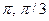 ]
] - f=x, g=y, A=[-1,1], B=(-3,3)
- f=2x/(x+3), g=y/3, A=(3,4], B=[-2,5)
2.
- A={-1, -2,-3,-5,-7,-11, -13}, R=4x,G=y/2
- A=
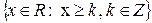 , R=(x-1)2, G=y
, R=(x-1)2, G=y
Практическая работа №3
Тема: Отношения.
Задание №1
Даны множества 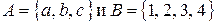 и два бинарных отношения:
и два бинарных отношения: 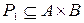 и
и 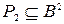 . Найдите Р1-1, Р2-1,
. Найдите Р1-1, Р2-1, 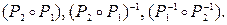 Определите, является ли отношение Р2 рефлексивным, транзитивным, симметричным, антисимметричным.
Определите, является ли отношение Р2 рефлексивным, транзитивным, симметричным, антисимметричным.
P1={(a,1); (a,3); (b,2); (c,1); (c,4)}
P2={(1,1); (1,3); (2,2); (2,1); (2,4); (3,3); (4,1); (4,4)}
Решение: По определению обратное отношение 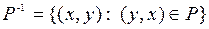 . Таким образом, Р1-1={(1,a); (3,a); (2,b); (1,c); (4,c)} и P2-1={(1,1); (3,1); (2,2); (1,2); (4,2); (3,3); (4,4); (1,4)}.
. Таким образом, Р1-1={(1,a); (3,a); (2,b); (1,c); (4,c)} и P2-1={(1,1); (3,1); (2,2); (1,2); (4,2); (3,3); (4,4); (1,4)}.
По определению композиции бинарных отношений
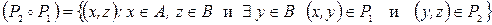
Таким образом, 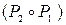 ={(a,1); (a,3); (b,2); (b,1); (b,4); (c,1); (c,3); (c,4)}.
={(a,1); (a,3); (b,2); (b,1); (b,4); (c,1); (c,3); (c,4)}.
Тогда 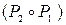 -1={(1,a); (3,a); (2,b); (1,b); (4,b); (1,c); (3,c); (4,c)}.
-1={(1,a); (3,a); (2,b); (1,b); (4,b); (1,c); (3,c); (4,c)}.
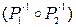 ={(1,a); (1,c); (3,a); (3,c); (2,b); (1,b); (4,b); (4,c)}
={(1,a); (1,c); (3,a); (3,c); (2,b); (1,b); (4,b); (4,c)}
Последние два множества совпадают, что и должно быть по свойствам композиции.
Отношение Р2 рефлексивно, т. к. в соответствии с определением рефлексивности 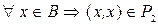 .
.
Отношение Р2 не является транзитивным, поскольку по определению транзитивности требуется, чтобы для любых пар (x, y) и (y, z), таких что (x, y) 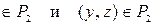 следовало бы, чтобы пара
следовало бы, чтобы пара 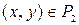 . Однако это не так. Например, пары (2,1) и (1,3) Î Р2, но пара (2,3) Ï Р2.
. Однако это не так. Например, пары (2,1) и (1,3) Î Р2, но пара (2,3) Ï Р2.
Отношение Р2 не является симметричным, т. к. по определению симметричности для любой пары (x, y) Î Р2 должно быть и (y, x) Î Р2 . Однако это не так. Например, пара (1,3)Î Р2 , но пара (3,1) Ï Р2.
Отношение Р2 антисимметрично, поскольку для любой пары (x, y) Î Р2 такой, что (y, x) Î Р2 обязательно следует, что x=y.
Задание №2
Дано бинарное отношение P Í ℕ2 и P = { (x, y): x mod y = 2 }, где «mod» – операция нахождения остатка от деления x на y.
Найдите область определения и область значений отношения Р.Является ли отношение Р рефлексивным, транзитивным, симметричным, антисимметричным? Является ли оно отношением эквивалентности или упорядоченности?
Решение: областью значений отношения Р является множество таких натуральных чисел y, что в остатке от деления на y может быть получено значение 2. В качестве такого делителя y можно взять любое натуральное число >2. Таким образом, пр2 Р = { y Î ℕ: y ³ 3 } – область значений.
Область определения отношения Р – это множество тех натуральных чисел x, для которых может быть получен остаток, равный 2, при делении на y ³ 3. Выразим x через y: x=k.y+2, где k=0,1,2,… и y ³ 3. Отсюда возможными значениями x являются числа: 2, 5, 6, 7, 8,… Таким образом, пр1 Р={2,5,6,7,8,9,…}=ℕ \ {1,3,4} – область определения.
Отношение Р не является рефлексивным, т. к. для всех x Î ℕ (x, x) Ï P. Действительно, "x Î ℕ Þ x mod x = 0.
Отношение Р не является транзитивным, т. к. существуют такие пары (x, y)ÎP и (y, z)ÎP, но (x, z)ÏP. Например, пары (7,5) и (5,3) обе 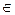 Р, но пара (7,3)ÏР, т. к. 7 mod 3 = 1.
Р, но пара (7,3)ÏР, т. к. 7 mod 3 = 1.
Отношение Р не является симметричным, поскольку существуют такие пары, что (x, y)ÎP , но (х, у)ÏР . Например , пара (7,5)ÎР , но (5,7)ÏР, т.к. 5 mod 7=5.
По определению антисимметричности для всех таких пар (х, у), что (у, х)ÎР и (х, у)ÎР обязательно следует, что х=у. Но для заданного отношения Р не существует пар (х, у) таких, что (х, у)ÎP и (у, х)ÎР, поскольку равенство (х mod y = y mod x =2) не выполняется ни при каких х, уÎℕ. Поэтому данное отношение Р является антисимметричным.
По набору свойств отношение Р не является ни отношением эквивалентности, ни отношением упорядоченности.
