Полем називається комутативне кільце, для будь-якого ненульового елемента якого існує обернений.

Зауваження. Нехай 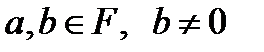. Тоді діленням елемента на елемент називається операція .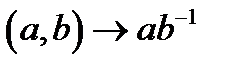

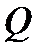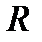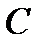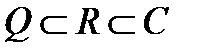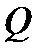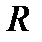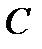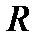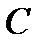Приклади: поле раціональних дробів , дійсних чисел і поле комплексних чисел . Очевидно, . Говорять, що є підполем (крім того, підполем поля ). З іншого боку, поля і називаються надполями або розширеннями поля .

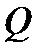Поле, що не є надполем ні для яких підполей називається простим (наприклад, поле 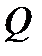- простуе).

Існують поля, що складаються із скінченного числа елементів. Такі поля називаються полями Галуа. Виявляється, число 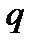елементів скінченного поля завжди є степенем деякого простого числа 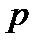: 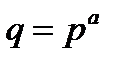. Поле Галуа, що складається з 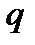елементів, позначається 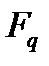або 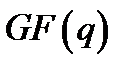. Оскільки мультиплікативна група 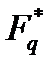поля 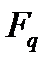складається з 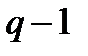елемента, то , .

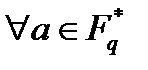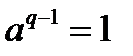Адитивна група поля 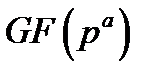має фундаментальну особливість: результат додавання будь-якого елемента поля 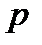раз самим із собою дорівнює нулю. Число 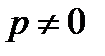називається характеристикою поля, якщо сума, що складається з 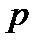одиниць дорівнює нулю і 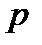- мінімальне число з такою властивістю. Характеристика поля 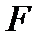позначається .

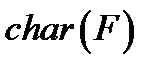Адитивній групі поля 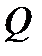такої властивості не має. У подібних випадках характеристика поля вважається рівною нулю.

11. Лінійні перетворення та матриці над полем.

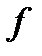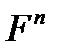
Відображення : 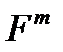називається лінійним оператором з 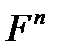у 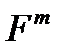, якщо виконуються наступні умови.

, , , .

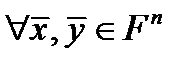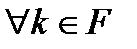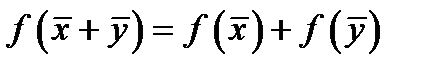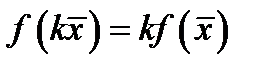Матрицею 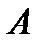розміру 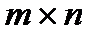над полем 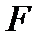називається прямокутна таблиця, що складається з 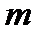рядків і 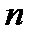стовпців і містить 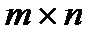елементів з .

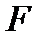Елемент 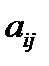матриці індексуються номером рядка 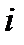та стовпця 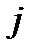, на перетину яких він знаходиться.

Транспонуванням матриці 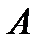розміру 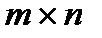називається операція побудови матриці 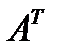(інше позначення - 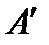) розміру 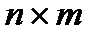, де .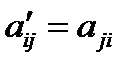

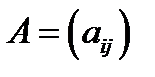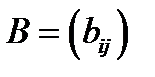Сумою матриць і розміру 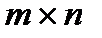називається матриця 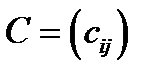, де 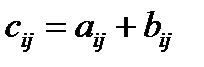. Множення матриці на константу виконується покомпонентно.

Лінійною формою над кільцем 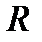з вектором змінних 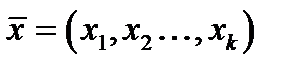і коефіцієнтами 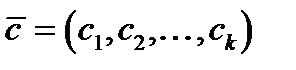, називається функція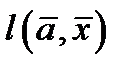 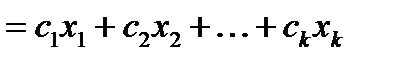. Для лінійної форми часто використовується позначення 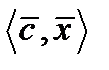. Зауважимо, що можливий випадок 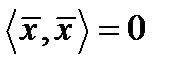, при .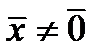

Добуток 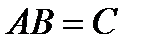матриці 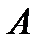розміру 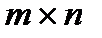на матрицю 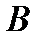розміру 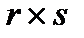визначено лише у випадку, коли 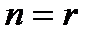і .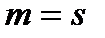

В окремому випадку множення матриці-рядка 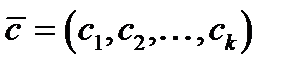на матрицю-стовпець 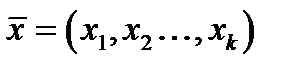, результат визначається як 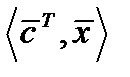(тобто, при цьому 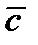розглядається як вектор).

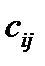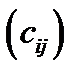
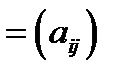
У загальному випадку елемент матриці 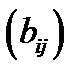визначається як 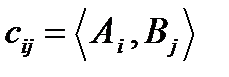, де 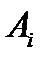- рядок матриці з номером , а 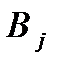- стовпець матриці 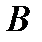з номером .

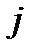Рангом матриці називається ранг системи її векторів-стовпців.

Теорема. Ранг матриці дорівнює рангу системи її векторів-рядків.

Матриця 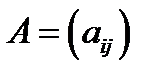розміру 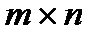називається квадратною, якщо 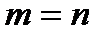. Кількість стовпців квадратної матриці називається її порядком. Діагоналлю з номером 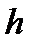квадратної матриці 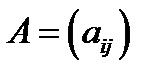порядку 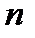називається підмножина її елементів виду 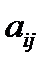, 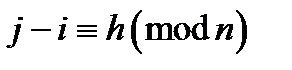. При 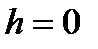, діагональ називається головною, всі інші діагоналі називаються побічними.

Множина квадратних матриць є некомутативним кільцем.

Нулем є матриця 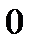, що складається з усіх нулів. Одиницею - матриця 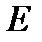, у якої всі елементи головної діагоналі дорівнюють одиниці, а інші елементи - нулю.

Множення квадратної матриці порядку 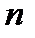на матрицю-стовпець можна розглядати як операцію над векторами. Така операція є лінійним перетворенням 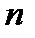- мірного векторного простору. Матриця називається оборотною, якщо вона здійснює взаємно однозначне перетворення.

Нехай 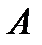- оборотна матриця. Матрицею оберненою до 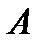називається матриця 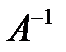, для якої виконуються умови .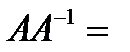

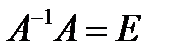12. Подільність цілих чисел. Алгоритм Евкліда.

Числа 1,2,3,…називаються натуральними. Число 0, а також числа виду 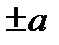, де 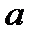натуральне число, називаються цілими числами. Відношення двох цілих чисел називається раціональним дробом і є записом результату ділення одного числа на інше. Ділення на нуль не визначено.Множина раціональних дробів є полем. Позначення .

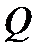Простим числом називається натуральне число, у якого є точно два нерівних натуральних дільники.

Основна теорема арифметики: кожне натуральне число єдиним, з точністю до порядку співмножників, чином представляється у виді добутку ступенів простих чисел.

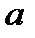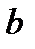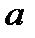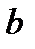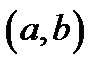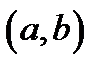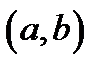
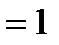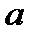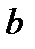Найбільшим спільним дільником двох цілих чисел і називається найбільше ціле число, що ділить як так і . Позначення: або НСД . Якщо НСД , то числа і називаються взаємно простими.

Найменшим спільним кратним натуральних чисел 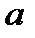і 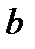називається найменше натуральне число, НОК 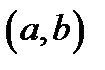, що ділиться як на 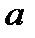так і на .

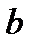Очевидно, НОК .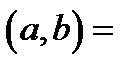

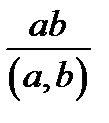Алгоритм Евклида для визначення НСД двох натуральних чисел 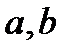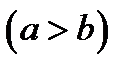. Основну роль грає операція ділення чисел з остачею, тобто представлення виду , .

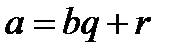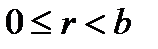Запишемо числа 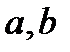. Знайдемо остачу 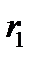від ділення 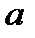на 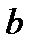, запишемо її слідом за 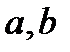: 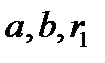. В отриманому списку розглянемо останні два числа.

Знайдемо остачу 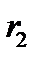від ділення першого з них на друге: 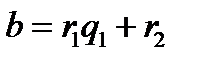, допишемо в список: . Діємо далі аналогічно, поки вперше (на -ому кроці) не виникне ситуація, коли 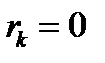. Тоді .

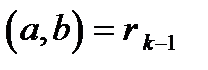13. Розширений алгоритм Евклида.

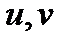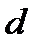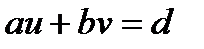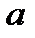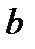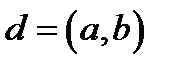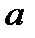Цей алгоритм призначений для пошуку лінійного представлення НСД, тобто цілочислового розв’язку , рівняння , > , , де і 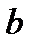також цілі.

Протокол роботи розширеного алгоритму Евкліда зручно записувати у вигляді таблиці:

Остачі						…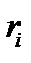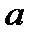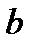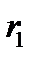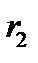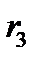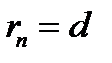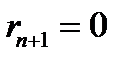
Частки						…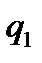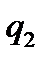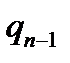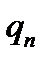
						…
						…

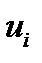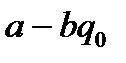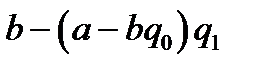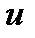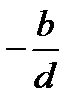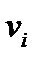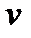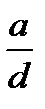Отримання нових значень компонент 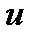наборів 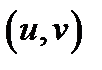показано в третьому рядку таблиці (клітинки виділені): з числа в першій клітинці віднімається число в другій клітинці, помножене на число, що стоїть справа від нього в другому рядку, результат записується в третю клітинку. Аналогічно виконуються операції для знаходження компонент 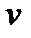у четвертому рядку.

14. Прості числа і основна теорема арифметики.

Натуральне число 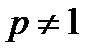називається простим, якщо воно не має додатних дільників, відмінних від 1 і 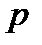. Всі інші числа називаються складеними.

Теорема (основна теорема арифметики). Будь-яке натуральне число 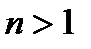або є простим числом, або його можна записати, причому єдиним чином (з точністю до порядку множників), у вигляді добутку простих чисел.

Канонічним розкладом (канонічною формою) складеного натурального числа 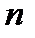називається представлення його у вигляді 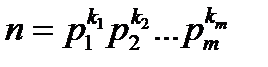.). Процес подання цілого числа 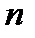у такому вигляді називають також факторизацією числа 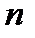. Якщо ж враховуються нульові показники степенів то такий розклад називається узагальненим канонічним розкладом.

Наслідок з основної теореми арифметики.Нехай 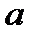і 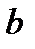– довільні натуральні числа, і нехай

,

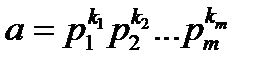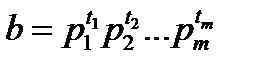
– їх узагальнені канонічні розклади ( 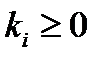, 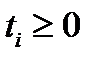). Тоді найбільший спільний дільник і найменше спільне кратне чисел 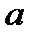і 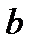відповідно мають вигляд:

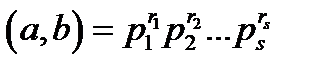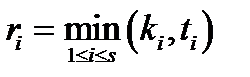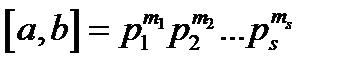, де ,

, де .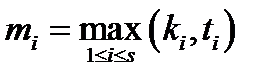

15. Многочлени над полями.

Многочлен над полем 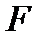- це функція виду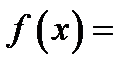 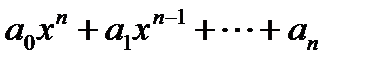, де 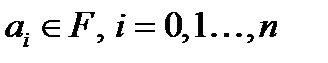, 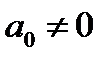. Ціле число 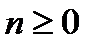називається степенем многочлена і позначається .

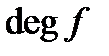Аналогічно визначається многочлен над комутативним кільцем. Множина 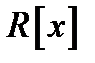усіх многочленів від однієї змінної над комутативним кільцем 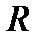також є кільцем.

Якщо 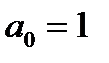, по многочлен називається зведеним (нормованим, унітарним). Многочлен 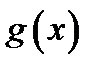називається дільником многочлена 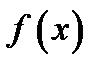, якщо існує многочлен 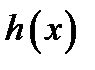, такий, що , .

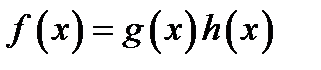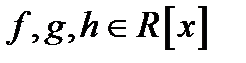Спільним дільником двох многочленів називається многочлен, що ділить обидва зазначені многочлени.

Тому дільники многочленів визначаються з точністю до константи.

Найбільшим спільним дільником 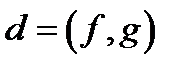двох многочленів 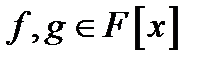називається многочлен 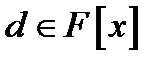, такий, що для будь-який загальний дільник 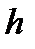многочленів 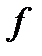і 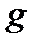ділить .

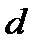Звичайно, в якості 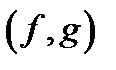вибирається нормований многочлен.

Визначення. Многочлен ненульового степеня називається незвідним, якщо він ділиться тільки на константи і сам на себе.

16. Алгоритм Евкліда для многочленів.

Операція ділення з остачею відповідає запису виду 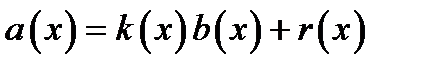, 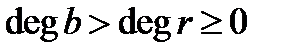. Якщо вперше на 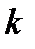-ому кроці виявляється, що 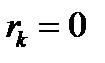, процес обчислення остач від ділення зупиняється і .

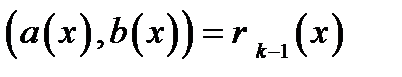17. Означення і властивості конгруенцій.

Кожне ціле число 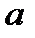можна розділити з остачею на натуральне число : , .

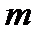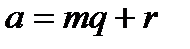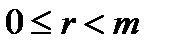Остача від ділення числа на 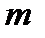називається лишком (у даному випадку – лишком числа 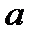за модулем 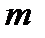). Операція, що співставляє числу 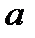його лишок за модулем 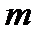, називається зведенням 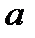за модулем .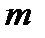