Влияние движения судна на точность гирокомпаса
Обратимся теперь к изучению работы гирокомпаса на подвижном основании. Вначале рассмотрим случай, когда объект перемещается с постоянной скоростью на постоянном курсе.
В этом случае управляющие моменты будут такими же, как при работе гирокомпаса на неподвижном основании, а гироскопические моменты дополнятся моментами, зависящими от скорости и курса судна. Для составления дифференциальных уравнений движения ЧЭ воспользуемся выражениями гироскопических моментов, полученными во втором разделе для ГК с НУ.
Тогда вместо системы (3.5) получим:
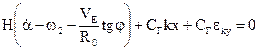
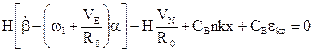(3.5)
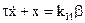
Определим положение динамического равновесия гирокомпаса в рассматриваемом случае, пока не делая никаких предложений о характере сигналов коррекции.
Полагая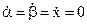 
, получим:
,
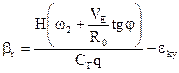(3.6)
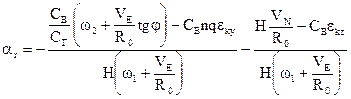
Ясно, что при отсутствии сигналов коррекции, т.е.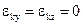 
, гирокомпас с косвенным управлением имел бы такие же девиации, как ГК с НУ. Из (3.6) видно, каким образом следует формировать сигналы коррекции для исключения девиации гирокомпаса.
Очевидно, должно быть:
; 
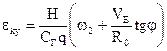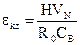(3.7)
При этом, как следует из (3.5), все гироскопические моменты, вызываемые движением судна, будут скомпенсированы.
Следовательно, на вход вычислительного устройства должны подаваться значения широты плавания, скорости и истинного курса судна.
Поскольку фактически известным является не истинный, а компасный курс, на первый взгляд его ввод приведет к неточной компенсации скоростной девиации. Однако при более тщательном рассмотрении можно убедиться, что это не так.
Действительно, перепишем второе уравнение системы (3.5) без допущения о малости координаты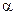 
:
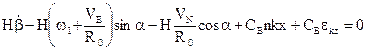(3.8)
Пусть сигнал коррекции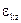 
формируется в функции компасного курса:
.
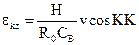Заменяя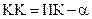 
, получим:
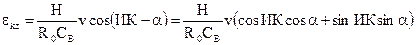
После подстановки последнего выражения в уравнение (3.8)
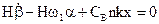(3.9)
Уравнение (3.9) подобно второму уравнению системы (3.5) для случая неподвижного основания.
Таким образом, ввод коррекции по вертикальной оси прецессии в функции компасного курса полностью исключает скоростную девиацию гирокомпаса. При этом его направляющий момент [второй член в уравнении (3.9)] не зависит от скорости судна.
В этом состоит основное преимущество гирокомпаса с КУ перед всеми обычными гирокомпасами.
Далее рассмотрим влияние на гирокомпас ускоренного движения судна. При этом будем полагать, что сигналы коррекции в соответствии с формулами (3.7) введены. Тогда движение судна влияет на гирокомпас только через индикатор горизонта, поскольку все гироскопические моменты, вызываемые скоростью судна, скомпенсированы. Так как индикатор горизонта работает как физический маятник, ускорению судна в направлении оси чувствительности соответствует сила инерции, равная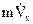 
и направленная в сторону, противоположную ускорению. Добавляя эту силу в уравнение индикатора горизонта, имеем:
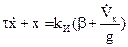(3.10)
Уравнения движения чувствительного элемента при этом остаются по форме такими же, как на неподвижном основании:
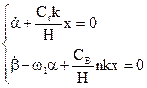(3.11)
Если время маневра мало по сравнению с периодом колебаний гирокомпаса, то можно принять, что координата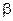 
за время маневра практически не изменяется и сохраняет свое значение 
.
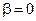В этом случае уравнение (3.10) может быть переписано в виде
Решение этого уравнения для случая равноускоренного движения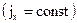 
как известно, будет
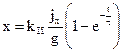
Видно, что сигнал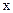 
, вызванный ускорением 
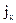, нарастает постепенно, от нуля при 
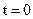до некоторого значения к моменту окончания маневра. При этом скорость нарастания сигнала зависит от постоянной времени 
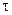. Чем больше величина 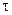, тем медленнее происходит увеличение сигнала 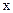. Если 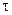достаточно велико, то за время маневра сигнал практически не успевает достичь такой величины, при которой происходит срабатывание управляющих двигателей. В этом случае чувствительный элемент остается свободным от ускорений и инерционная девиация у гирокомпаса не возникает. Однако, как мы видели при рассмотрении устойчивости колебаний, величина 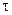не может быть чрезмерно большой. Поэтому при достаточно продолжительном времени маневра некоторый сигнал все же будет снят с индикатора горизонта.
В результате отработки двигателем этого сигнала гирокомпас начнет прецессировать вокруг вертикальной оси. Как видно из первого уравнения системы (3.11), скорость инерционной прецессии равна
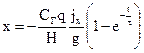
К моменту окончания маневра tм у гирокомпаса накопится инерционная погрешность
,
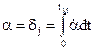которая затем начнет убывать по закону затухающих колебаний гирокомпаса.
Более строгий вывод инерционной девиации может быть получен непосредственным решением систем уравнений (3.10) и (3.11).
Перейдем теперь к методам исключения инерционной девиации у рассматриваемого гирокомпаса.
Прежде всего заметим, что поскольку уравнения движения чувствительного элемента не зависят от скорости судна, при изменении скорости положение равновесия гирокомпаса не меняется. Это значит, что в данном случае понятие апериодических переходов гирокомпаса к новому положению равновесия не имеет смысла.
В рассматриваемом приборе применяется принципиально иной метод исключения инерционных девиаций. Кардинальной мерой служит устранение самой причины их возникновения, а именно — компенсация силы инерции, приложенной к индикатору горизонта при ускоренном движении объекта. В менее точных приборах используется еще более простой способ, описанный ниже.
Для компенсации силы инерции в вычислительном устройстве гирокомпаса производится вычисление действующего ускорения. Эта операция может быть выполнена интегрированием северной составляющей скорости, снимаемой с лага (предполагается, что лаг имеет малую инерционность).
Сигнал, пропорциональный вычисленному ускорению, используется для возбуждения в индикаторе горизонта некоторой дополнительной силы, действующей на рабочее тело в направлении, противоположном силе инерции. Такую силу можно получить, например, с помощью электромагнитного устройства, смонтированного в индикаторе горизонта так, что его силовые линии концентрируются вдоль оси ОХ. В этом случае гирокомпас будет полностью освобожден от влияния ускорения.
Менее точный способ состоит в следующем. В индикаторе горизонта контактные ограничители 7 разрывают цепь индикатора горизонта при смещении чувствительного элемента 1 на некоторую малую величину (см. рис. 3.3). Эта величина достаточна, однако, для того, чтобы обеспечить нормальную работу гирокомпаса при отсутствии ускорения.
При критическом смещении чувствительного элемента индикатор горизонта самоотключается и гирокомпас теряет связь с Землей. В то же время сохраняется коррекция, компенсирующая вращение Земли и движение судна, т. е. гирокомпас превращается в своеобразный гироскоп направления. За время маневра он не успевает существенно отклониться от первоначального направления, а так как положение равновесия гирокомпаса не меняется, то после включения индикатора горизонта появляется лишь весьма незначительная затухающая ошибка.
Предполагается, что этот метод пригоден при скоростях объекта до 200 узлов.
Характерная особенность гирокомпаса с косвенным управлением состоит в том, что при непосредственной компенсации ускорения не накладываются никакие ограничения на величину периода и характер свободных колебаний гирокомпаса. Иначе говоря, колебания гирокомпаса продолжают оставаться затухающими и выключатель затухания не требуется. Период колебаний может быть выбран достаточно малым, с тем чтобы обеспечить быстрое приведение гирокомпаса в меридиан. Если же используется способ ограничителей, то желательно, напротив, увеличить период собственных колебаний, с тем чтобы снизить скорость инерциальной прецессии гирокомпаса на рабочем участке характеристики индикатора горизонта. В некоторых разработанных конструкциях гирокомпаса значение периода собственных колебаний увеличено до 180 мин.
Отметим, что большая инерционность индикатора горизонта (т. е. существенная величина постоянной времени 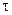) весьма эффективно устраняет влияние кратковременных ускорений, возникающих, например, при вибрациях и ударах корпуса судна.