Есептің қойылымы және негізгі ұғымдар.
V-бөлім. Сандық интегралдау
Арапайым квадратурлық формулалар
Есептің қойылымы және негізгі ұғымдар.
Бұл бөлімде 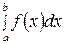 анықталған интегралды жуықтап есептеу әдістері қарастырылады, мұндағы
анықталған интегралды жуықтап есептеу әдістері қарастырылады, мұндағы 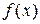 - берілген интеграл астындағы функция,
- берілген интеграл астындағы функция, 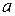 және
және 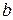 - интегралдың төменгі және жоғарғы шектері.
- интегралдың төменгі және жоғарғы шектері.
Сандық интегралдау деп интеграл астындағы функцияны жуықтаушы функциямен алмастыру арқылы анықталған интегралды есептеу процесін айтады.
Интегралды жуықтап есептеу формулаларын квадратурлық формулалар деп атайды.
Алдымен математикалық анализ курсынан белгілі анықталған интеграл ұғымын енгізейік. 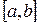 кесіндіде
кесіндіде 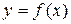 үзіліссіз функциясы берілсін.
үзіліссіз функциясы берілсін. 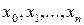 нүктелер арқылы
нүктелер арқылы 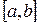 кесіндісін n қарапайым
кесіндісін n қарапайым 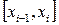
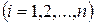 кесінділерге бөлеміз, мұндағы
кесінділерге бөлеміз, мұндағы 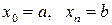 .
. 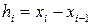 арқылы әр қарапайым кесіндінің ұзындықтарын белгілейміз. Әр қарапайым кесіндіден кез-келген
арқылы әр қарапайым кесіндінің ұзындықтарын белгілейміз. Әр қарапайым кесіндіден кез-келген 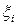
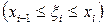 нүктесін таңдап алып, осы нүктедегі функцияның
нүктесін таңдап алып, осы нүктедегі функцияның 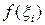 мәні мен кесінді ұзындығының көбейтіндісін анықтайық, яғни
мәні мен кесінді ұзындығының көбейтіндісін анықтайық, яғни 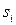 :
:
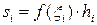 (5.1.1)
(5.1.1)
Барлық қарапайым кесінділер үшін алынған 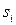 шамалардың қосындысын құрайық:
шамалардың қосындысын құрайық:
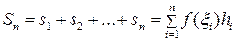 . (5.1.2)
. (5.1.2)
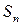 қосындысын интегралдық қосынды деп атайды.
қосындысын интегралдық қосынды деп атайды. 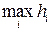 арқылы
арқылы 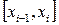
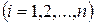 кесінділердің ұзындығының ең үлкенін белгілейік.
кесінділердің ұзындығының ең үлкенін белгілейік.
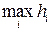 нөлге ұмтылған кезде (5.1.2) интегралдық қосындының ақырлы шегі бар және
нөлге ұмтылған кезде (5.1.2) интегралдық қосындының ақырлы шегі бар және 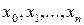 нүктелерді
нүктелерді 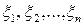 нүктелерді таңдау тәсіліне тәуелсіз болсын. Онда осы шекті
нүктелерді таңдау тәсіліне тәуелсіз болсын. Онда осы шекті 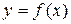 функциясның
функциясның 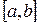 кесіндідегі анықталған интегралы деп атайды және
кесіндідегі анықталған интегралы деп атайды және 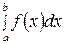 деп белгілейді, яғни
деп белгілейді, яғни
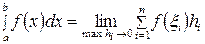 (5.1.3)
(5.1.3)
Теорема (Анықталған интегралдың бар болу туралы). Егер 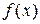 функциясы
функциясы 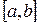 кесіндіде үзіліссіз болса, онда интегралдық қосындының шегі бар және ол
кесіндіде үзіліссіз болса, онда интегралдық қосындының шегі бар және ол 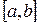 кесіндісін қарапайым кесінділерге бөлуіне,
кесіндісін қарапайым кесінділерге бөлуіне, 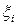 нүктесін таңдау тәсіліндеріне тәуелсіз.
нүктесін таңдау тәсіліндеріне тәуелсіз.
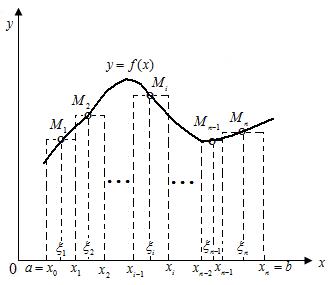
5 сурет
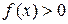 жағдайы үшін енгізілген ұғымдардың геометриялық мағынасы 5-суретінде көрсетілген.
жағдайы үшін енгізілген ұғымдардың геометриялық мағынасы 5-суретінде көрсетілген. 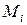 нүктелердің абциссалары ретінде -
нүктелердің абциссалары ретінде - 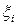 , ординаталары ретінде -
, ординаталары ретінде - 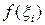 мәндері болып табылады. (5.1.1) өрнегі қарапайым тіктөртбұрыштардың (суретте штрих сызықтармен белгіленген) ауданын сипаттайды, ал (5.1.2) интегралдық қосынды осы тіктөртбұрыштар арқылы құрылған фигураның ауданын береді.
мәндері болып табылады. (5.1.1) өрнегі қарапайым тіктөртбұрыштардың (суретте штрих сызықтармен белгіленген) ауданын сипаттайды, ал (5.1.2) интегралдық қосынды осы тіктөртбұрыштар арқылы құрылған фигураның ауданын береді. 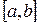 кесіндісін қарапайым кесінділерге бөліктейтін
кесіндісін қарапайым кесінділерге бөліктейтін 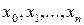 нүктелер санын көбейткен сайын және
нүктелер санын көбейткен сайын және 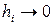 кезде, фигураның жоғарғы шекарасы (сынық)
кезде, фигураның жоғарғы шекарасы (сынық) 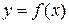 қисығымен беттеседі.
қисығымен беттеседі.
Жоғарыдан 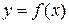 қисығымен, төменнен х осімен және
қисығымен, төменнен х осімен және 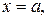
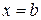 түзулермен шенелген фигураны қисықсызықты трапеция деп атайды. Осыдан анықталған интегралдың геометриялық мағынасы: ол жоғарыда сипатталған қисықсызықты трапецияның ауданы болып табылады.
түзулермен шенелген фигураны қисықсызықты трапеция деп атайды. Осыдан анықталған интегралдың геометриялық мағынасы: ол жоғарыда сипатталған қисықсызықты трапецияның ауданы болып табылады.
Интеграл астындағы функция аналитикалық түрде берілген кезде, көп жағдайда оны Ньютон-Лейбниц формуласымен есептеуге болады:
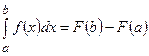
мұнда 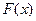 –
– 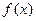 функцияның алғашқы функциясы. Бірақ екі негізгі жағдайларда бұл формуланы қолдануға келмейді: 1) интеграл астындағы функция күрделі түрде беріліп, оның алғашқы функциясын белгілі әдістермен, формулалармен есептеуге келмесе; 2) интеграл астындағы функция кесте түрінде берілсе. Бұл жағдайларда сандық интегралдау әдістері қолданылады. Олар интеграл астындағы функцияны қарапайым өрнектермен, мысалы көпмүшелікпен, жуықтауға негізделген.
функцияның алғашқы функциясы. Бірақ екі негізгі жағдайларда бұл формуланы қолдануға келмейді: 1) интеграл астындағы функция күрделі түрде беріліп, оның алғашқы функциясын белгілі әдістермен, формулалармен есептеуге келмесе; 2) интеграл астындағы функция кесте түрінде берілсе. Бұл жағдайларда сандық интегралдау әдістері қолданылады. Олар интеграл астындағы функцияны қарапайым өрнектермен, мысалы көпмүшелікпен, жуықтауға негізделген.
Сандық интегралдаудың қарапайым әдістерін қарастырайық:
