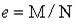Предельные состояния и расчет внецентренно растянутых и внецентренно сжатых элементов

Предельные состояния внецентренно растянутых и жестких внецентренно сжатых элементов определяются несущей способностью по прочности или развитием пластических деформаций, а гибких внецентренно сжатых - потерей устойчивости.

Расчет на прочность. Предельные состояния по прочности внецентренно растянутых (растянуто-изогнутых) и внецентренно сжатых (сжато-изогнутых) элементов конструкций при динамических воздействиях, а также элементов конструкций, выполненных из сталей высокой прочности с расчетным сопротивлением R >580 МПа, определяются достижением наибольшими фибровыми напряжениями расчетного сопротивления. Их расчет выполняется по упругой стадии работы материала по формуле:

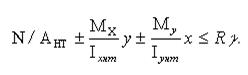
(3.37)

Для внецентренно сжатых и внецентренно растянутых элементов из пластичных сталей с пределом текучести до 580 МПа при действии статических нагрузок предельное состояние по прочности определяется с учетом развития пластических деформаций.

Развитие пластических деформаций при наличии момента и продольной силы так же, как и в изгибаемых элементах, приводит к образованию шарнира пластичности, но при этом положение нейтральной оси в процессе развития пластических деформаций смещается (рис. 3.17). При увеличении момента и продольной силы на одной из сторон стержня фибровые напряжения достигают предела текучести и затем останавливаются в своем развитии.

Напряжения в прочих фибрах (угол наклонной части эпюры напряжений) продолжают расти, пока, наконец, напряжения на другой стороне стержня не достигнут предела текучести, после чего пластичность распространяется на все фибры сечения (см. рис. 3.17). Очевидно, что разность площадей эпюр напряжений, умноженная на , равна предельной продольной силе

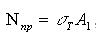
(3.38)

где A1 и A2 - площади частей сечения, показанные на рис. 3.17.

Площадь определяет одну составляющую пары изгибающего момента; такая же площадь на другой стороне сечения должна определять вторую составляющую этой пары. Отсюда предельный момент

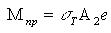(3.39)

где е - расстояние между центрами площадей A1.

Таким образом, в пластической стадии напряжения от продольной силы и момента можно условно разделить. Напряжения от продольной силы занимают среднюю часть - сечения A1= A-2A2, а напряжения от момента края на площадях A2.

При развитии шарнира пластичности соотношение предельных продольных сил, отвечающих наличию момента Nмпр и его отсутствию N0пропределяется отношением , а соотношение предельных моментов, отвечающих наличию продольной силы Mnпр и ее отсутствию M0пр, определяется отношением .

Для прямоугольного сечения связь между этими отношениями выражается параболой (рис. 3.18).

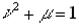(3.40)

Для двутавровых сечений эта зависимость ближе к линейной и может быть выражена:

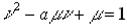(3.41)

где а - коэффициент, определяемый характером распределения материала по сечению двутавра.

Аналогичный подход может быть использован и при работе стержня на совместное действие двух моментов Мх и Му и нормальной силы.

Образование шарнира пластичности приводит к неограниченному росту перемещений. Для обеспечения эксплуатационной пригодности конструкций проверяют прочность элементов при совместном действии изгиба и осевой силы, как и изгибаемых элементов, по критерию ограниченных пластических деформаций

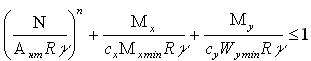
Коэффициенты п, сх и су учитывают степень развития пластических деформаций и зависят от формы сечения. Численные значения этих коэффициентов при 8=3 для некоторых типов сечения приведены в прил. 5.

Проверка устойчивости внецентренно сжатых (сжато-изгибаемых) элементов. При приложении сжимающей силы с эксцентрицитетом стержень работает как внецентренно сжатый. При одновременном приложении продольной осевой силы и поперечной нагрузки, вызывающей изгиб, стержень будет сжато-изгибаемым. Хотя в том и в другом случае по сечению развиваются напряжения одинакового вида, вызванные продольной силой и моментом, работа стержня в этих случаях несколько отличается главным образом в предельном состоянии при малых гиб-костях. Однако в целях упрощения практических методов расчета (в небольшой запас) сжато-изгибаемые стержни при рассмотрении критического состояния потери устойчивости приравниваются к внецентренно сжатым, имеющим эксцентрицитет .