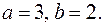Расстояние от точки до плоскости

Пусть задана точка 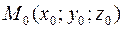и плоскость 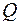своим уравнением

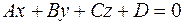. Расстояние от точки 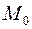до плоскости 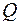находится по формуле

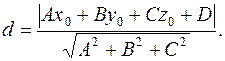(3.6)

Пример 32.Вычислить расстояние от точки 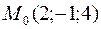до плоскости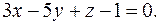

Решение. Для заданной плоскости вектором нормали будет вектор 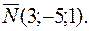Подставим в формулу (3.6)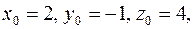

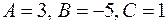и вычислим расстояние от точки 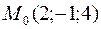до плоскости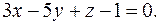

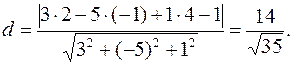
Взаимное расположение двух плоскостей

Пусть заданы две плоскости 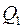и :

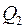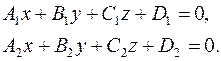
Если плоскост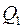и и 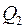перпендикулярны, то таковы же их нормали, т.е 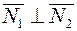(и наоборот). Но тогда 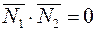, т.е. 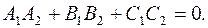Полученное равенство есть условие перпендикулярности двух плоскостей 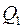и .

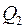Если плоскост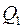и и 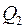параллельны, то будут параллельны и их нормал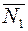и и 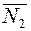(и наоборот). Но тогда координаты векторов пропорциональны: 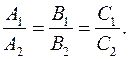Это и есть условие параллельности двух плоскосте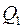й

и .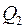

Пример 33.Перпендикулярны ли плоскост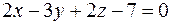и и ?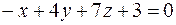

Решение. Выпишем векторы нормали к плоскостям 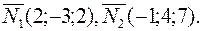Вычислим их скалярное произведение 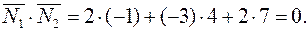Следовательно, плоскости перпендикулярны.

ПРЯМАЯ В ПРОСТРАНСТВЕ

Общие уравнения прямой

Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей:

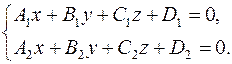(4.1)

Каждое уравнение этой системы определяет плоскость. Если плоскости не параллельны, то система определяет прямую 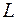как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. Уравнения (4.1) называют общими уравнениями прямой.

Канонические уравнения прямой

Пусть 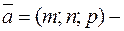направляющий вектор прямо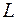й и 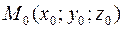- точка, лежащая на этой прямой. Вектор 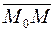, соединяющий точку 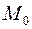с произвольной точкой 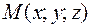прямой 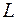, параллелен вектору 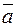. Поэтому координаты вектора 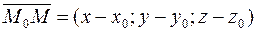и вектора 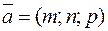пропорциональны:

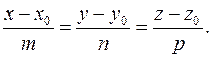(4.2)

Уравнения (4.2) называются каноническими уравнениями прямой в пространстве.

Пример 34.Написать уравнение прямой, проходящей через точку 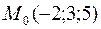параллельно вектору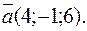

Решение. Воспользуемся уравнением (4.2):

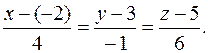Итак, получаем каноническое уравнение прямой

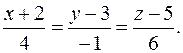
Уравнение прямой в пространстве, проходящей через две точки

Пусть прямая 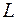проходит через точки 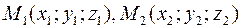. В качестве направляющего вектора 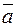можно взять вектор

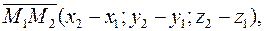т.е. 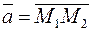(рис. 11)

Рис. 11

Следовательно, 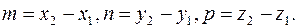Поскольку прямая проходит через точку 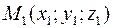, то согласно уравнениям (4.2), уравнение прямой имеет вид

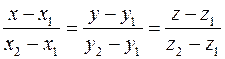(4.3)

Пример 35.Написать уравнение прямой, проходящей через точки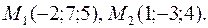

Решение. Воспользовавшись уравнением (4.3), получим:

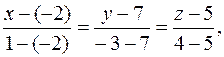или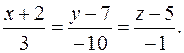

КРИВЫЕ ВТОРОГО ПОРЯДКА

Эллипс

Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек 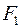и 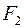этой плоскости, называемых фокусами, есть величина постоянная.

При этом не исключается совпадение фокусов. Очевидно, если фокусы совпадают, то эллипс представляет собой окружность.

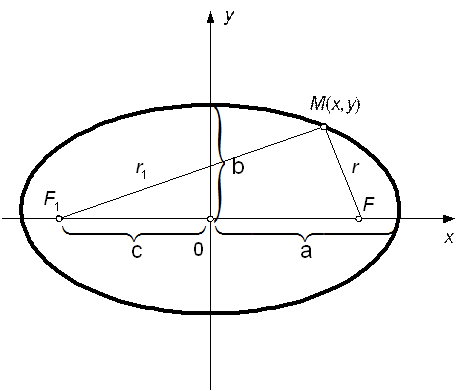
Рис. 12

Каноническое уравнение эллипса 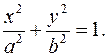(5.1)

Величины 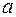и 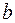называются соответственно большой и малой полуосями эллипса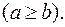

Замечание. В предельном случае, когда 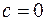эллипс представляет собой окружность радиуса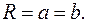

Пусть 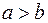, тогда фокусы 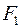и 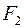находятся на оси 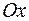на расстоянии 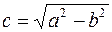от центра.

Определение. Эксцентриситетом эллипса называется величина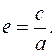

Замечание. Учитывая связь величины 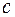с длинам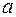и и 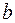большой и малой полуосей эллипса, легко получить следующее выражение для эксцентриситета :

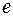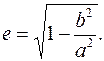
Пример 36. Написать каноническое уравнение эллипса, если известно, что:

1) расстояние между фокусами равно 8, а малая полуось 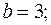2) большая полуось 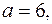а эксцентриситет 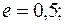3) расстояние между фокусами равно 6, а эксцентриситет 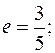4) расстояние между фокусами равно 6, а 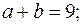5) расстояние между фокусами равно 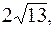а

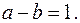
Решение.1) Так как расстояние между фокусами равно 8 имеем 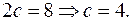Найдем большую полуось эллипса по формуле 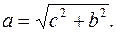Имеем 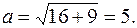Тогда каноническое уравнение эллипса имеет вид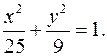

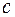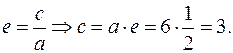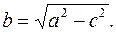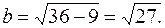2) Найдем из формулы Определим меньшую полуось эллипса по формуле Тогда Каноническое уравнение эллипса имеет вид

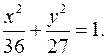
3) По условию 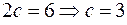. По формуле 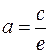найдем большую полуось эллипса 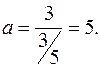Меньшая полуось 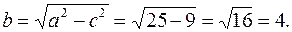Каноническое уравнение эллипса

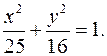
4) По условию 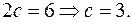Из равенства 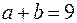выразим 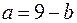и подставим в равенство 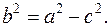Получим 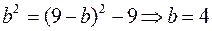и 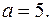Каноническое уравнение эллипса

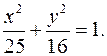
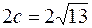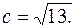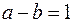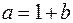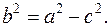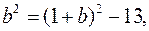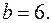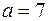5) Из условия находим Из равенства выразим и подставим в равенство Получим откуда Тогда . Каноническое уравнение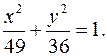

Пример 37.Эллипс проходит через точк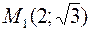и и 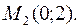Написать его каноническое уравнение.

Решение. Так как эллипс проходит через точки 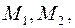их координаты удовлетворяют каноническому уравнению эллипса. Имеем

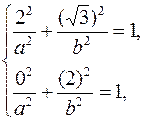
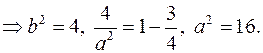
Уравнение эллипса имеет вид

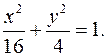
Гипербола

Определение. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек 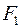и 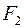, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы 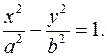(5.2)

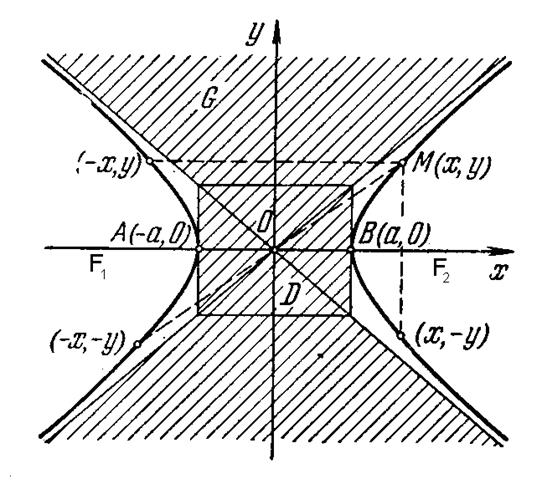
Рис.13

Гипербола, заданная уравнением (5.2), симметрична относительно осей координат (рис. 13). Она пересекает ось 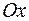в точках 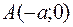и 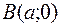− вершинах гиперболы и не пересекает ось 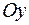. Параметр 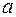называется вещественной полуосью, 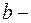мнимой полуосью. Параметр 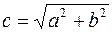есть расстояние о фокуса до центра. Отношение 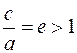называется эксцентриситетом гиперболы.

Эксцентриситет для гиперболы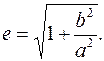

Прямые 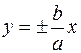называются асимптотами гиперболы.

Пример 38. Построить гиперболу 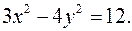Найти 1) действительную и мнимую полуоси; 2) координаты фокусов; 3) эксцентриситет; 4) уравнения асимптот.

Решение. 1) Запишем уравнение гиперболы в канонической форме 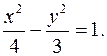Действительная полуось гиперболы 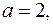мнимая полуось 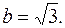2) Найдем 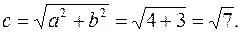Фокусы гиперболы 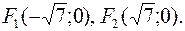3) Эксцентриситет 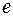найдем по формуле 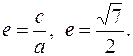4) Уравнения асимптот 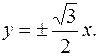Построим гиперболу.

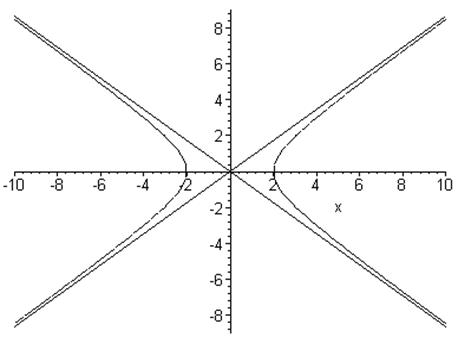
Рис. 14

Парабола

Определение. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки 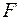равно расстоянию до некоторой фиксированной прямой этой плоскости. Указанная в определении точка 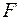называется фокусом параболы, а фиксированная прямая- директрисой параболы.

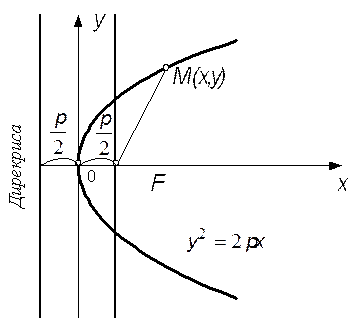
Рис. 15

Отсюда 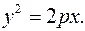Это уравнение называется каноническим уравнением параболы. Величина 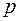называется параметром параболы.

Пример 39.Построить параболу 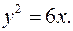Найти 1) координаты фокуса; 2) уравнение директрисы.

Решение. Из уравнения параболы получаем 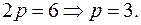Значит, парабола имеет фокус 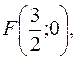а уравнение директрисы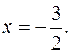

Построим параболу

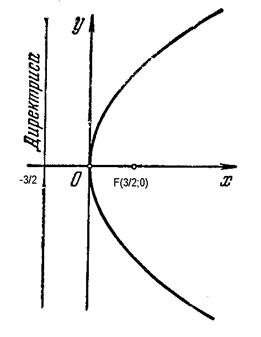
Рис. 16

Пример 40.Установить вид кривой второго порядка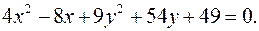

Решение. Сгруппируем слагаемые с переменной 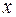и с переменной .

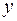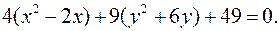Выделим полные квадраты: 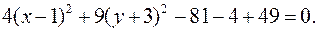Имеем 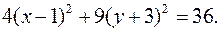Разделив обе части равенства на 36, окончательно получаем

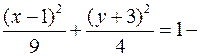уравнение эллипса с центром в точке 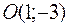и полуосями