Теоремы о связности орграфа

Теорема 1.Орграф является сильносвязным, тогда и только тогда, когда в нем существует остовный циклический маршрут (остовным маршрутом называется маршрут, проходящий через все вершины графа).

Теорема 2. Орграф является односторонним тогда и только тогда, когда в нем существует остовный маршрут.

Теорема 3. Орграф является слабым тогда и только тогда, когда в нем существует остовный полумаршрут.

ТИПЫ КОМПОНЕНТ СВЯЗНОСТИ

Сильная компонента - это максимальный (по включению) сильно связанный подграф исходного графа.

Односторонняя компонента - это максимальный (по включению) односторонне связанный подграф исходного графа.

Слабая компонента - это максимальный (по включению) слабый подграф исходного графа.

Пример:

Поскольку отношение взаимной достижимости двух вершин орграфа является отношением эквивалентности (рефлексивно, симметрично и транзитивно), то оно разбивает множество всех вершин на классы эквивалентности, т. е. такие подмножества вершин орграфа, что подграфы, порожденные этими подмножествами вершин, являются сильными компонентами.

Конденсацией называется такой орграф G*, вершины которого соответствуют сильным компонентам S₁,S₂,…, S_k орграфа G, и пара (S_i, S_j) в G* является дугой тогда и только тогда, когда в орграфе G существует хотя бы одна дуга, начало которой принадлежит компоненте S_i, конец - S_j.

Пример:

5.6

АЛГОРИТМ ПОСТРОЕНИЯ КОНДЕНСАЦИИ

1. Построить матрицу достижимости:

R = ||r_ij||, i, j = , где

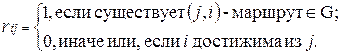
2. Построить матрицу контрдостижимости:

Q = ||qij||, i, j = , где

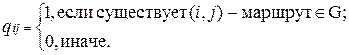
Замечание. Матрица контрдостижимости Q может быть получена с помощью транспонирования матрицы R: Q = R^Т.

3. Построить матрицу взаимной достижимости:

S = ||s_ij||, i, j = , где

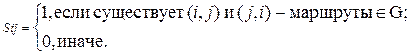
S = R * Q ( где * - оператор поэлементного умножения матриц R и Q: s_ij = r_ij * q_ij ).

4. Определить сильные компоненты: привести матрицу S к блочно-диагональному виду (перестановкой ее строк и столбцов). Вершины, составляющие каждый блок - сильные компоненты.

5. Каждой сильной компоненте поставить в соответствие одну вершину конденсации. Построить множество дуг (по определению конденсации). Полученный орграф – конденсация исходного графа.

Пример:

R

Q

S

Преобразуем матрицу S к блочно-диагональному виду:

S

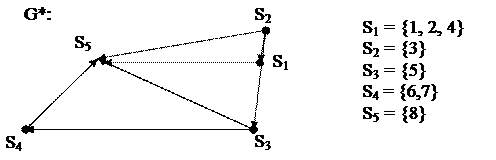
БАЗА И АНТИБАЗА

Базаорграфа G - наименьшее (относительно включения) подмножество вершин B (B Ì V), удовлетворяющее условию: любая вершина v Î V\B достижима из какой-либо вершины w Î B.

Антибаза орграфа G - наименьшее ( относительно включения) подмножество вершин B' (B'Ì V) такое, что любая вершина vÎ B' достижима из какой- либо вершины w Î V\ B'.

АЛГОРИТМ ПОСТРОЕНИЯ БАЗЫ

В орграфе всегда существует база. Вершины, полустепени захода которых равны нулю, принадлежат базе.

База бесконтурного графа состоит только из вершин, полустепени захода которых равны нулю.

Сильные компоненты орграфа, в которые не входят дуги из других сильных компонент, соответствуют вершинам с нулевыми полустепенями захода в орграфе G* и являются базовыми компонентами.

Алгоритм.

1. Построить конденсацию G* орграфа G.

2. Выделить в ней базовые компоненты; им в конденсации соответствует вершины с нулевой полустепенью захода.

3. Из каждой базовой компоненты произвольно выбрать по одной вершине.

Замечание. База определяется не единственным образом, исключая ациклический граф.

В рассмотренном выше примере база: B={v₃}.