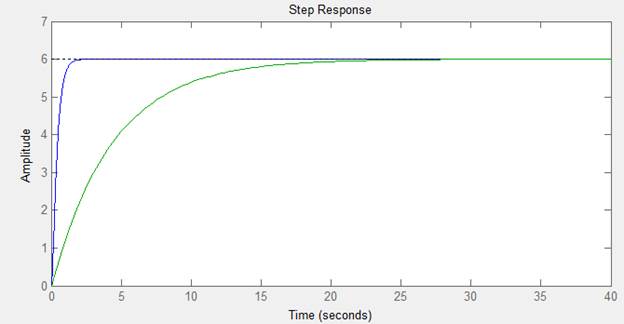
По переходной характеристике определить показатели качества (перерегулирование, время переходного процесса, колебательность).
Подготовительный этап 1.1.
Перейти от записи системы в виде передаточной функции к записи в виде уравнений состояния: – аналитический
0,04 *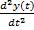 
+ 0,44 * 
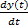+ y(t) = 6*x(t)
= 
+ 
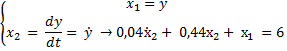
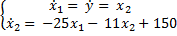
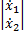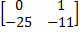
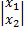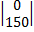
y = |0 1|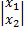
– с использованием Control System Toolbox (проверить полученный результат)
>> W = tf([6],[0.04 0.44 1])
Transfer function:
---------------------
0.04 s^2 + 0.44 s + 1
>> [A B C D] = tf2ss([6],[0.04 0.44 1])
A =
-11 -25
1 0
B =
C =
0 150
D =
1.2. Определить нули и полюса системы – с использованием Control System Toolbox.
>> W_zp=zpk(W)
W_zp =
-------------------
(s+7.791) (s+3.209)
Continuous-time zero/pole/gain model.
>> z=zero(W)
z =
Empty matrix: 0-by-1
>> p=pole(W)
p =
-7.7913
-3.2087
Построить в Simulink модель для исследования колебательного звена 2 порядка с заданными параметрами K, T и z.
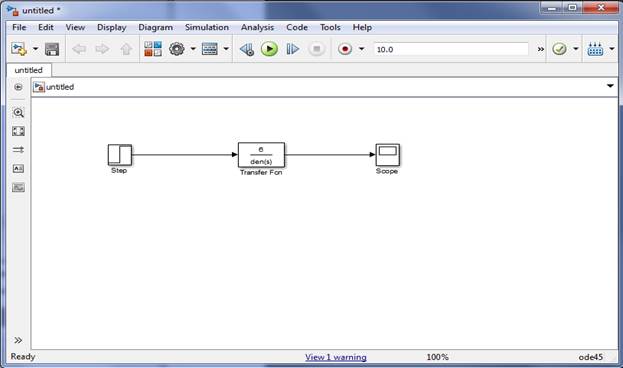
Написать скрипт на языке Matlab, который по данным переходного процесса будет определять показатели качества (перерегулирование, время переходного процесса, колебательность)
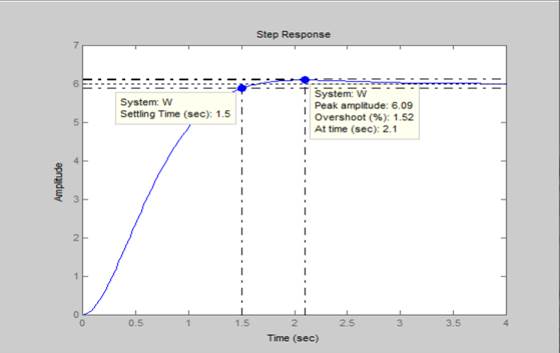
время переходного процесса 1.5 c
перерегулирование = 1.52%
Определить передаточную функцию системы, полученной из заданной путем ее замыкания через единичную отрицательную обратную связь (ООС), перейти от записи системы в виде передаточной функции к записи в виде уравнений состояния, определить нули и полюса системы.
· передаточную функцию системы ООС
>> W0=1
W0 =
>> R1=feedback(W,W0,-1)
R1 =
---------------------
0.04 s^2 + 0.44 s + 7
· в виде уравнений состояния
>> [A B C D]=tf2ss([6],[0.04 0.44 7])
A =
-11 -175
1 0
B =
C =
0 150
D =
= 
+
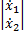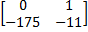
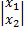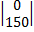
· определить нули и полюса системы
>> z=zero(R1)
z =
Empty matrix: 0-by-1
>> p=pole(R1)
p =
-5.5000 +12.0312i
-5.5000 -12.0312i
Построить в Simulink модель для исследования полученной замкнутой системы с ООС.
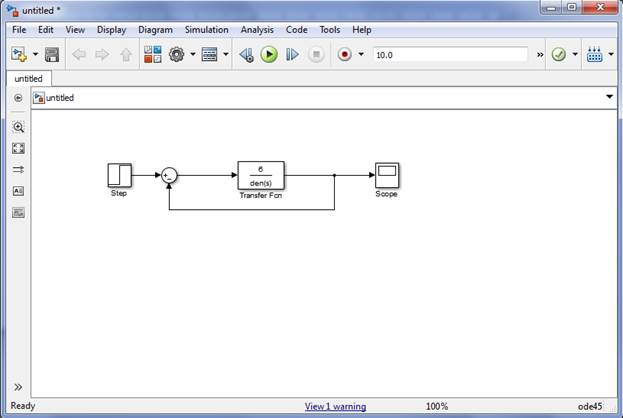
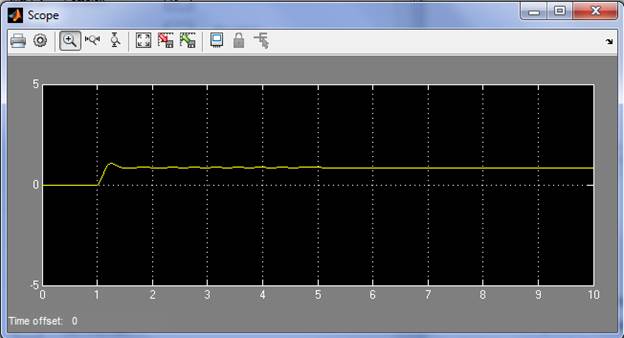
1.7. Определить передаточную функцию системы, полученной из заданной путем ее замыкания через положительную обратную связь (ПОС) с коэффициентом Kос , построить в Simulink модель для исследования полученной замкнутой системы.
>> R2=feedback(W,W0,1)
R2 =
---------------------
0.04 s^2 + 0.44 s - 5
Continuous-time transfer function.
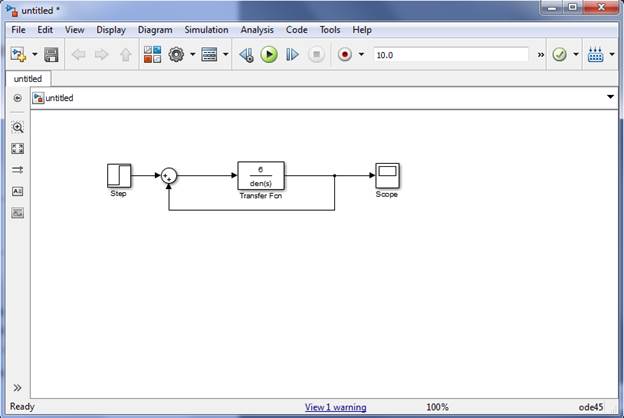
1.8. Определить значение Kос , приводящее замкнутую систему с ПОС на границу устойчивости. Cистему с ПОС на границу устойчивости когда урарнение
2. Моделирование временных характеристик звена
2.1. Построить переходную функцию звена:
– с использованием Simulink (без использования Control System Toolbox);
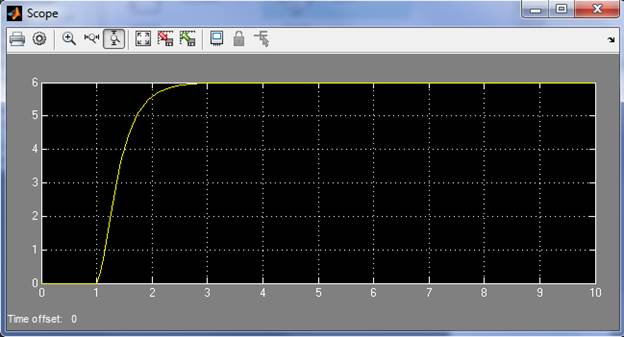
– с использованием Control System Toolbox (без использования Simulink).
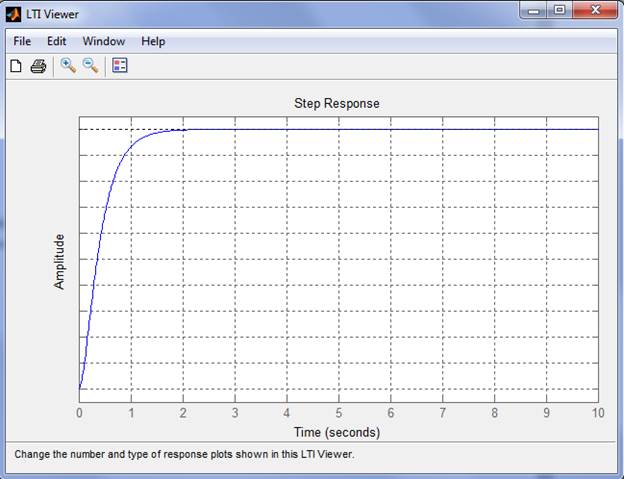
По переходной характеристике определить показатели качества (перерегулирование, время переходного процесса, колебательность).
время переходного процесса 1.38 c
перерегулирование = 0%
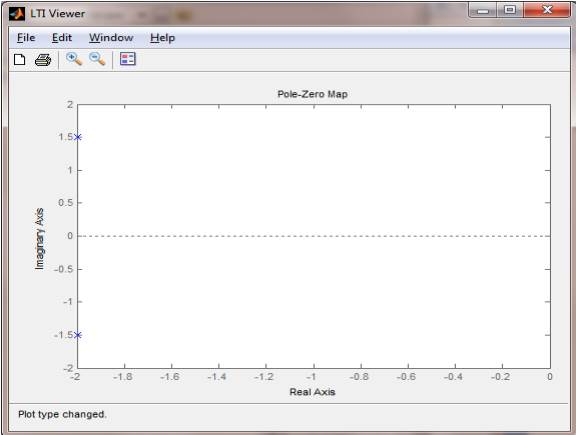
2.3. Исследовать влияние заданного параметра (K, T или z) на вид переходной функции, рассмотреть следующие значения параметра: 10% от исходного, 50% от исходного, 100% от исходного, 150% от исходного, 200% от исходного, 1000% от исходного. Для сравнения переходных функций результаты совместить на одном графике.
>> W=tf([6],[0.04 0.44 1]);
>> D1=tf([6],[0.04 0.044 1]);
>> ltiview(W,D1)
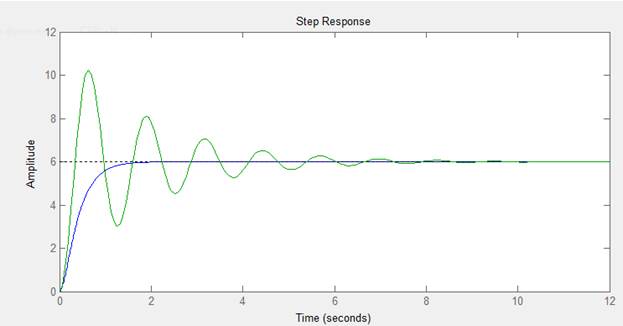
>> D2=tf([6],[0.04 0.22 1]);
>> ltiview(W,D2)
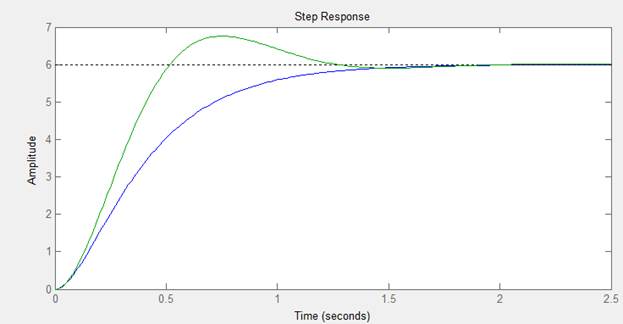
>> D3=tf([6],[0.04 0.44 1]);
>> ltiview(W,D3)
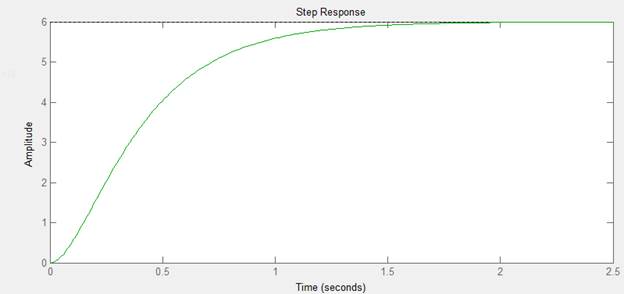
>> D4=tf([6],[0.04 0.66 1]);
>> ltiview(W,D4)
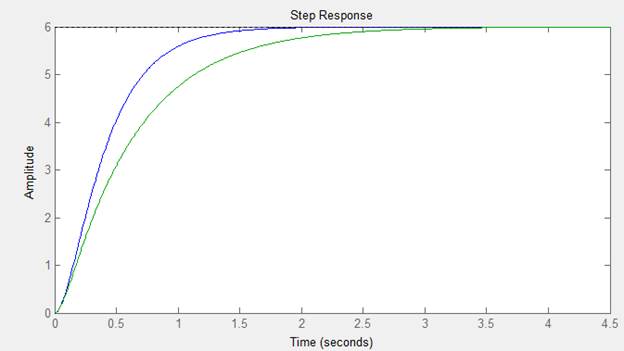
>> D5=tf([6],[0.04 0.88 1]);
>> ltiview(W,D5)
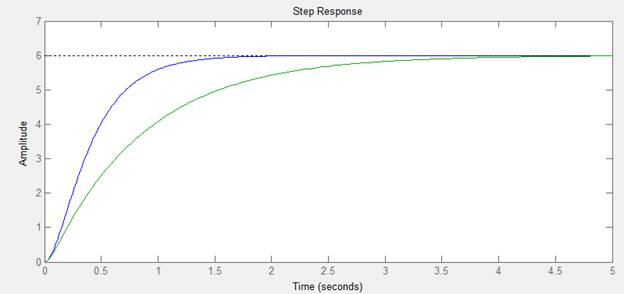
>> D6=tf([6],[0.04 4.4 1]);
>> ltiview(W,D6)
