Анализ сложной линейной электрической цепи постоянного тока
Расчётно-графическая работа № 3
Содержание
1.Краткие теоретические сведения
2. Задание на расчет
3. Примеры расчета лестничной цепи
4. Контрольные вопросы
1. Краткие теоретические сведения
Электрической цепью называют совокупность тел и сред, образующих замкнутые пути для протекания электрического тока.
Обычно физические объекты и среду, в которой протекает электрический ток, упрощают до условных элементов и связей между ними. Тогда определение цепи можно сформулировать как совокупность различных элементов, объединенных друг с другом соединениями или связями, по которым может протекать электрический ток.
Элементами электрической цепи являются источники электрической энергии, активные и реактивные сопротивления.
Связи в электрической цепи изображаются линиями и по смыслу соответствуют идеальным проводникам с нулевым сопротивлением.
Связи элементов электрической цепи обладают топологическими свойствами, т.е. они не изменяются при любых преобразованиях, производимых без разрыва связей.
Для описания топологических свойств электрической цепи используются топологические понятия, основными из которых являются узел, ветвь и контур. Пример такого преобразования показан на рис. 1.
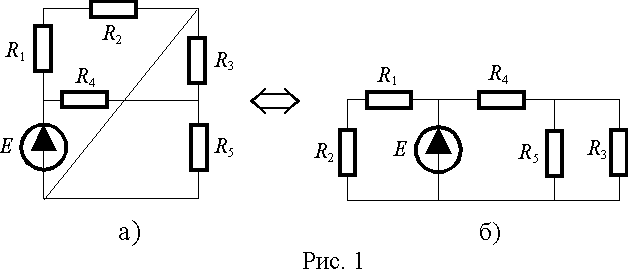
Рис. 1.
Узломэлектрической цепи называют место (точку) соединения трех и более элементов.
Ветвьюназывают совокупность связанных элементов электрической цепи между двумя узлами.
Контуром(замкнутым контуром) называют совокупность ветвей, образующих путь, при перемещении вдоль которого мы можем вернуться в исходную точку, не проходя более одного раза по каждой ветви и по каждому узлу.
По определению различные контуры электрической цепи должны отличаться друг от друга по крайней мере одной ветвью.
Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Первый закон Кирхгофа
Алгебраическая сумма токов в узле электрической цепи равна нулю:
При этом токи, направленные к узлу, обычно записываются со знаком «плюс», а токи, направленные от узла, - со знаком «минус».
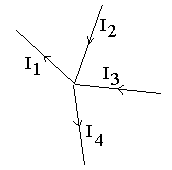-I1+ I2+ I3- I4 = 0
Рис. 2.
Второй закон Кирхгофа
Алгебраическая сумма падений напряжений в ветвях любого замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре.
Направление обхода контура выбираем произвольно (в примере против часовой стрелки).
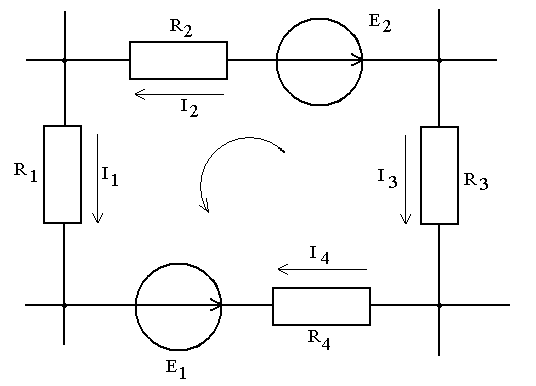I1R1+I2R2-I3R3-I4R4=E1-E2
Рис.3
Примечание: знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Сложной будем называть разветвленную электрическую цепь, содержащую несколько источников электрической энергии.
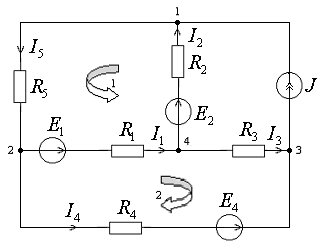
Рис. 4.
Будем считать заданными параметры источников ЭДС, источников тока и сопротивления приемников. Неизвестными являются токи ветвей, не содержащих источников тока.
Условными положительными направлениями токов задаемся произвольно.
Введем обозначения:
k – число узлов схемы
m – число ветвей, не содержащих источников тока
В рассматриваемом примере k = 4, m = 5.
Расчет и анализ сложной электрической цепи основан на уравнениях, составляемых по 1 и 2 законам Кирхгофа, в количестве, достаточном для решения системы. Все уравнения в системе должны быть независимыми.
Число независимых уравнений, составляемых по 1 закону Кирхгофа, на единицу меньше числа узлов:
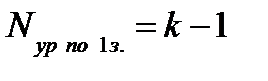
Число независимых уравнений, составляемых по второму закону Кирхгофа:
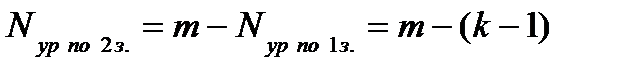
Независимость уравнений по второму закону Кирхгофа будет обеспечена, если контуры выбирать таким образом, чтобы каждый последующий контур отличался от предыдущего хотя бы одной новой ветвью.
Для контура, содержащего ветвь с источником тока, уравнение не составляется.
Направление обхода – произвольное.
Таким образом, порядок анализа сложной цепи с применением законов Кирхгофа следующий:
1) выбирают произвольно положительные условные направления токов в ветвях;
2) составляют (k-1) независимых уравнений по первому закону Кирхгофа.
3) выбирают произвольно направления обхода независимых контуров,
4) составляют m-(k-1) независимых уравнений по второму закону Кирхгофа,
5) решают совместно полученную систему уравнений.
Метод контурных токов
Введем новые условные (фиктивные) неизвестные, называемые «контурными токами».
«Контурный» ток замыкается по соответствующему контуру.
Составляются уравнения по 2-му закону Кирхгофа. Для того чтобы уравнения были независимыми, каждый последующий контур должен отличаться от предыдущих хотя бы одной новой ветвью.
Для контура, содержащего ветвь с источником тока, уравнение не составляется.
Пример выбора контурных токов показан на рисунке. Направления контурных токов выбираются произвольно. Ток источника тока J считается известным контурным током.
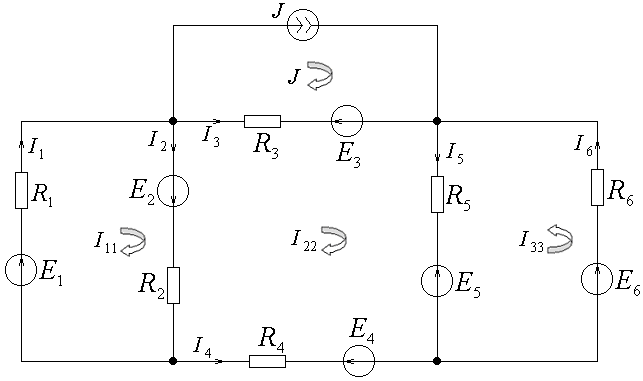
Рис. 5.
При использовании данного метода уравнения составляются только по второму закону Кирхгофа.
Метод контурных токов позволяет сократить число совместно решаемых в системе уравнений до
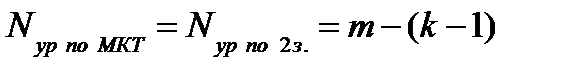
При этом учитывается, что падение напряжения на отдельных участках цепи создаются совместным действием контурных токов, проходящих через данные участки.
Уравнение для К-го контура любой схемы по методу контурных токов записывается как:
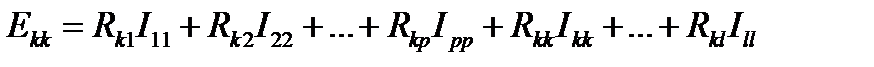
Здесь I11, I22, Ipp, Ikk, Ill,… - контурные токи 1-го, 2-го, р-го, к-го, l-го контуров,
Ekk - алгебраическая сумма ЭДС всех ветвей, составляющих к-ый контур,
Rkk - арифметическая сумма сопротивлений ветвей, составляющих рассматриваемый к-ый контур. Значения Rkk всегда положительны.
Rk1, Rk2, …, Rkp, Rkl - сопротивления ветвей, смежных между соответственно к-ым и первым, к-ым и вторым, к-ым и l-ым и т.д. контурами,
Rkp>0, если направления токов Ipp, Ikk через рассматриваемую ветвь совпадают. В противном случае Rkp<0.
Система уравнений по методу контурных токов сравнительно легко решается с помощью определителей.
После решения системы и определения контурных токов I11, I22, I33переходим к определению токов отдельных ветвей.
Ток какой-либо ветви определяется как алгебраическая сумма контурных токов через данную ветвь. Со знаком «плюс» будем записывать контурный ток, совпадающий по направлению с током данной ветви.
Баланс мощностей
Уравнение энергетического баланса:
Σ RI2 = Σ EI
Произведение записываются с «+», если направления ЭДС и тока совпадают, и с «-», если направления противоположны.
2. Задание на расчет
1. Составить уравнения по законам Кирхгофа.
2. Определить токи во всех ветвях цепи методом контурных токов.
3. Проверить баланс мощностей цепи.
4. Письменно ответить на контрольные вопросы.
Варианты схем
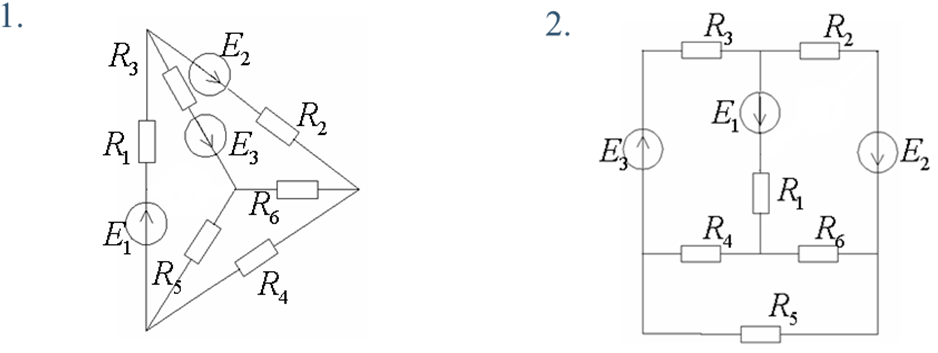
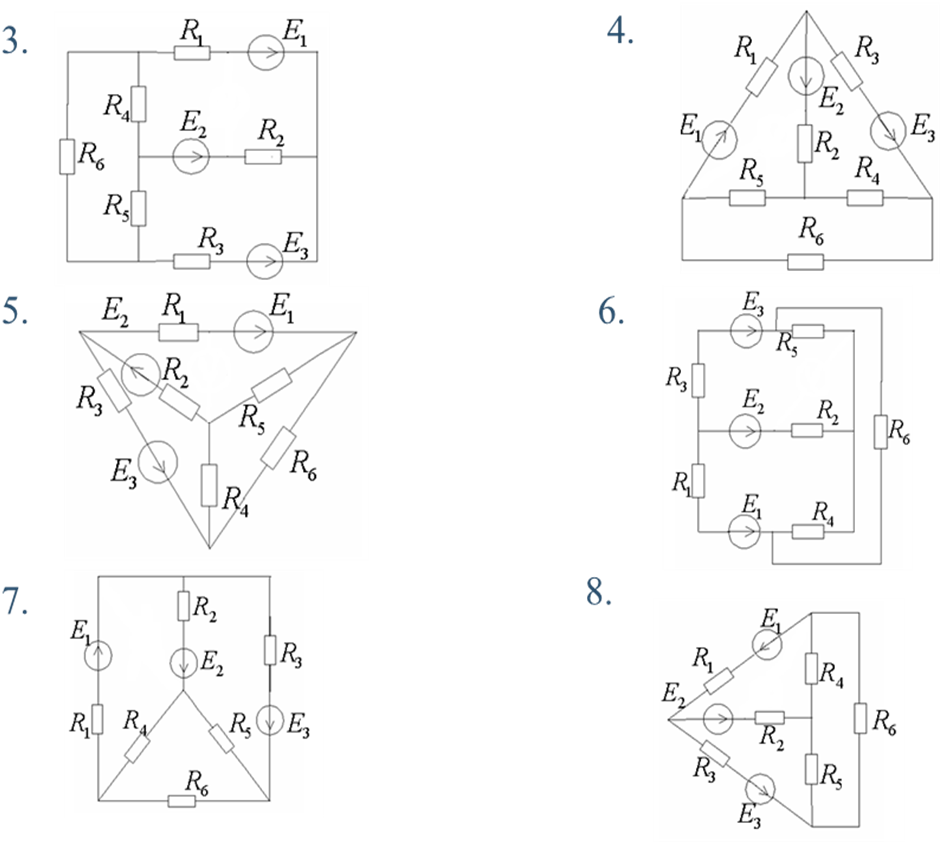
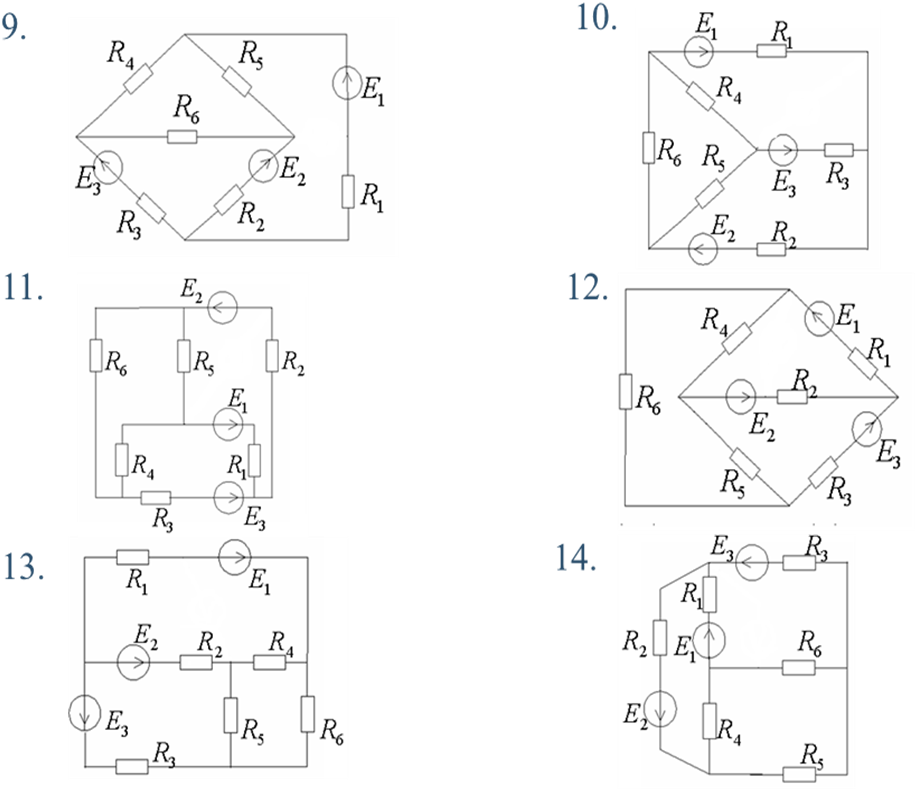
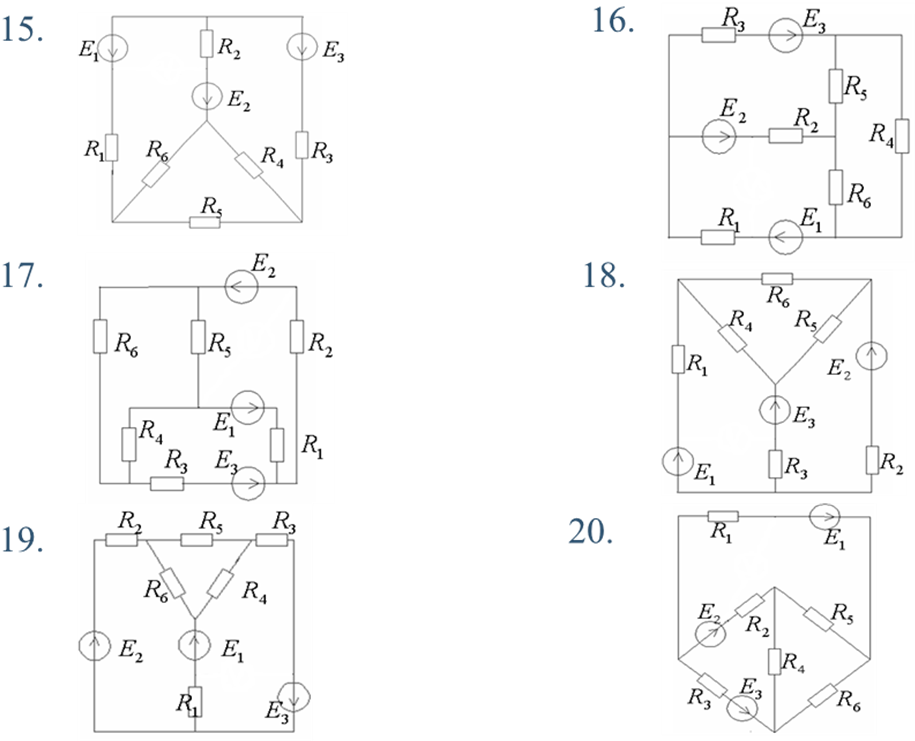
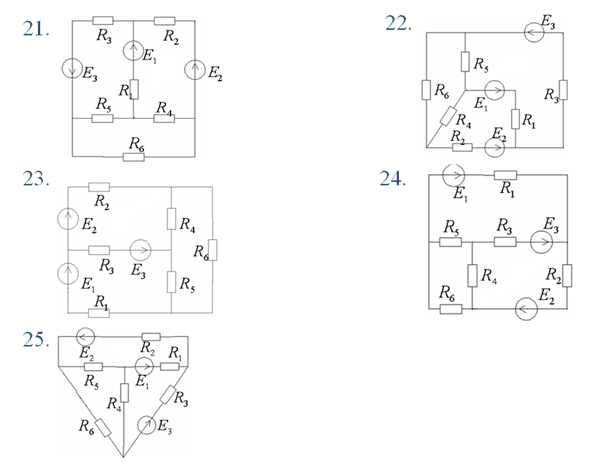
Таблица значений
| № варианта | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | E1, В | E2,В | E3, В |
| 1.5 | |||||||||
| 2.5 | |||||||||
| 3.5 | |||||||||
| 2.5 | |||||||||
| 3.5 | |||||||||
| 3.5 | |||||||||
| 1.2 | |||||||||
| 3.5 | |||||||||
| 4.2 | |||||||||
3. Пример расчета
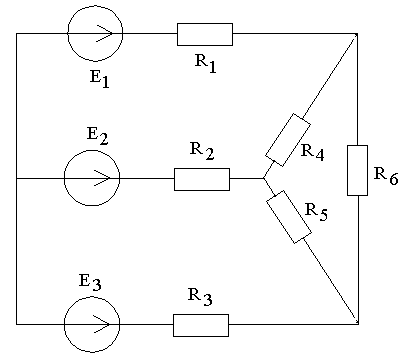 | Дано: R1=1 ОМ, R2=0,5 Ом, R3=0,4 Ом, R4=R5=R6=3 Ом, Е1=120 В, Е2=60 В, Е3=140 В 1. Составить уравнения по законам Кирхгофа; 2. Определить токи во всех ветвях цепи методом контурных токов; 3. Проверить баланс мощностей цепи. |
1. Составление уравнений по законам Кирхгофа
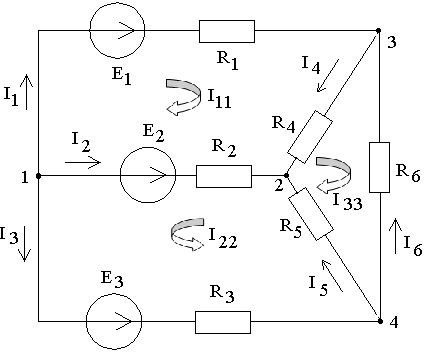
Произвольно выбираем положительные условные направления токов в ветвях и обход контура:
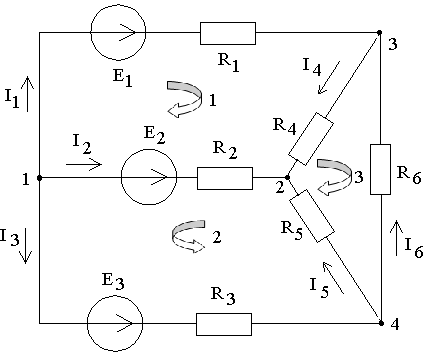
В рассматриваемом примере:
число узлов k = 4,
число ветвей m = 6;
число уравнений по первому закону Кирхгофа:
4-1=3,
число уравнений по второму закону Кирхгофа:
6-(4-1)=3.
Уравнения по первому закону Кирхгофа имеют следующий вид:
для узла 1: -I1-I2-I3=0
для узла 2: I2+I4+I5=0
для узла 3: I1-I4+I6=0
Уравнения по второму закону Кирхгофа имеют вид:
для контура 1: I1R1 - I2R2 + I4R4 = E1 - E2
для контура 2: - I2R2 + I3R3 + I5R5 = - E2 + E3
для контура 3: - I4R4 + I5R5 - I6R6 = 0
Решая полученную систему из 6 уравнений, получаем значения 6 неизвестных токов:
I1 = 6,3 А I2 = - 30,9 А
I3 = 24,6 А I4 = 12,6 А
I5 = 18,3 А I6 = 6,3 А
В результате решения значение второго тока оказалось отрицательным, значит действительное направление этого тока противоположно выбранному условному положительному направлению.
2. Определение токов во всех ветвях цепи методом контурных токов
Вводим новые неизвестные – контурные токи I11, I22, I33 и составляем уравнения для данных контуров по второму закону Кирхгофа:
E1-E2=(R1+R2+R4)I11+R2I22-R4I33
-E2+E3=(R2+R3+R5)I22+R2I11+R5I33
0=(R4+R5+R6)I33-R4I11+R5I22
Подставляя известные значения ЭДС и сопротивлений, решаем систему из трех уравнений.
Результат:
I11 =6,8 А,
I22 = 24,36 А,
I33 = -5,74 А
Определяем токи ветвей:
I1 = I11= 6,8 А I2= -I11-I22= -31,1 А
I3= I22= 24,36 А I4= I11-I33= 12,54 А
I5= I22+I33= 18,62 А I6= -I33= 5,74 А
3. Проверка баланса мощностей
R1I12+R2I22+R3I32+R4I42+R5I52+R6I62= = E1I1+E2I2+E3I3
Поставляем значения и определяем:
2365,56 = 2360,4
4. Контрольные вопросы
1. При каких условиях две цепи называют эквивалентными?
2. Что называют эквивалентным преобразованием цепи?
3. Как называются два обязательных этапа метода эквивалентных преобразований цепи?
4. Что понимается под понятием «определяющая величина»?
5. В качестве критерия правильности выполнения расчета используется соблюдение уравнений Кирхгофа. Как следует выбрать узел схемы для составления уравнения по первому закону Кирхгофа?
6. В качестве критерия правильности выполнения расчета используется соблюдение уравнений Кирхгофа. Как следует выбрать контур схемы для составления уравнения по второму закону Кирхгофа?
7. В качестве критерия правильности выполнения расчета можно использовать уравнение баланса мощностей. Как выглядит такое уравнение для рассмотренных примеров 1 и 2?