Градиенттің қасиеттері
1) 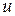 өрісінің градиенті мен
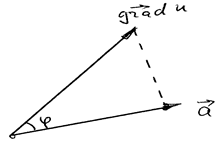
өрісінің градиенті мен 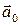 векторы арасында бұрышы
векторы арасында бұрышы 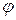 деп белгілейік, онда (3) тегі скаляр көбейтіндіні мына
деп белгілейік, онда (3) тегі скаляр көбейтіндіні мына 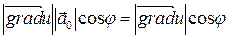 түрінде жазуға болады, бұл
түрінде жазуға болады, бұл 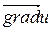 -дың
-дың 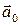 векторына проекциясы болады. Демек,
векторына проекциясы болады. Демек, 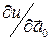
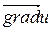 векторының
векторының 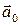 -ге проекциясымен дәл келеді:
-ге проекциясымен дәл келеді:
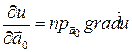 (5)
(5)
2) (5) формула бойынша 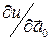
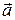 бағыты бойынша максимал болады,
бағыты бойынша максимал болады, 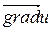 мен дәл келеді, өйткені бұл бағытта
мен дәл келеді, өйткені бұл бағытта 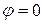 ,
, 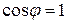 . Сондықтан
. Сондықтан 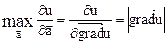 , градиент функцияның ең үлкен өсу бағытын береді, оның модулі осы бағыттағы туындыға тең.Скаляр өріс үшін – жергілікті жердің теңіз деңгейінен биіктігі – градиент жергілікті жердің ең үлкен тік көтерілімінің бағытын көрсетеді, ал оның модулі, немесе осы бағыттағы туындысы осы жердің көтерілімінің ең үлкен тангесіне тең. Егер кейбір жердің рельефі
, градиент функцияның ең үлкен өсу бағытын береді, оның модулі осы бағыттағы туындыға тең.Скаляр өріс үшін – жергілікті жердің теңіз деңгейінен биіктігі – градиент жергілікті жердің ең үлкен тік көтерілімінің бағытын көрсетеді, ал оның модулі, немесе осы бағыттағы туындысы осы жердің көтерілімінің ең үлкен тангесіне тең. Егер кейбір жердің рельефі 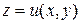 функциясымен берілсе, онда
функциясымен берілсе, онда 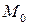 нүктесін бастапқы нүкте ретінде алып кез келген бағыттағы осы жердің тіктік көтерілімін есептеп шығаруға болады. Бұл үшін
нүктесін бастапқы нүкте ретінде алып кез келген бағыттағы осы жердің тіктік көтерілімін есептеп шығаруға болады. Бұл үшін 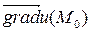 -ді тауып және оның бағыттағы проекциясын есептесек болды.
-ді тауып және оның бағыттағы проекциясын есептесек болды.
3) 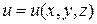 функциясының экстремаль нүктелеріндегі дербес туындылары (егер олар болса) нольге тең, бұл экстремумның қажеттілік шартымен туындайды. Градиенттің барлық координаталары
функциясының экстремаль нүктелеріндегі дербес туындылары (егер олар болса) нольге тең, бұл экстремумның қажеттілік шартымен туындайды. Градиенттің барлық координаталары 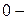 ге тең нүктелер өрістің сингуляр (айрықша) нүктелері деп аталады. Градиент
ге тең нүктелер өрістің сингуляр (айрықша) нүктелері деп аталады. Градиент 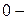 ге тең емес нүктелер регуляр нүктелер деп аталады. Географиялық картада төбелер, ойыс жерлер, өткелдер сингуляр да, ал басқа нүктелер регуляр нүктелер болады.
ге тең емес нүктелер регуляр нүктелер деп аталады. Географиялық картада төбелер, ойыс жерлер, өткелдер сингуляр да, ал басқа нүктелер регуляр нүктелер болады.
4) 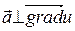 векторын алайық. Бұл жағдайда
векторын алайық. Бұл жағдайда 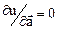 . Градиентке перпендикуляр бағыттағы шексіз аз жылжу мәні тұрақты болып қалады, демек осы бағытта
. Градиентке перпендикуляр бағыттағы шексіз аз жылжу мәні тұрақты болып қалады, демек осы бағытта 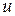 өрісінің деңгейлік беті өтеді. Келесі теорема орынды.
өрісінің деңгейлік беті өтеді. Келесі теорема орынды.
Теорема. 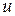 функциясының кез келген
функциясының кез келген  регуляр нүктесі арқылы оның деңгейлік бетіне
регуляр нүктесі арқылы оның деңгейлік бетіне 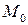 нүктесі арқылы өтетін жазықтық жүргізуге болады, бұл жазықтық
нүктесі арқылы өтетін жазықтық жүргізуге болады, бұл жазықтық 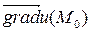 -ге перпендикуляр.
-ге перпендикуляр.
Градиенттің осы жазықтыққа нормаль вектор болатынын пайдаланып оның теңдеуін аламыз:
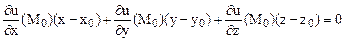 . (6)
. (6)
Екі айнымалы функция үшін 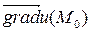 осы өрістің деңгей сызығының жанамасына перпендикуляр болады және бұл жанаманың (6) сияқты теңдеуін былай жазуға болады:
осы өрістің деңгей сызығының жанамасына перпендикуляр болады және бұл жанаманың (6) сияқты теңдеуін былай жазуға болады:
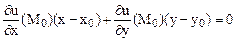 . (7)
. (7)
5) Градиенттің төменгі алгебралық қасиеттерін айта кетейік. Егер 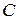 – тұрақты болса, онда
– тұрақты болса, онда 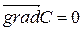 ,
, 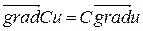 .
.
Екі 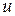 және
және 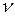 функциясы үшін
функциясы үшін 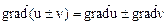 ,
, 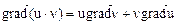 .
.
Дифференциалданатын 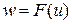 функция үшін:
функция үшін: 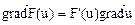 . Бұл қасиеттерді өріс пен градиенттің анықтамаларымен оңай дәлелдеуге болады. Өріс градиентіне, бағыт бойынша туындыға байланысты кейбір мысалдарды алып қарайық.
. Бұл қасиеттерді өріс пен градиенттің анықтамаларымен оңай дәлелдеуге болады. Өріс градиентіне, бағыт бойынша туындыға байланысты кейбір мысалдарды алып қарайық.
7-мысал. 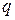 электр зарядынан пайда болған өрісті қарайық.
электр зарядынан пайда болған өрісті қарайық. 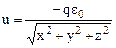 (
( 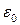 - электростатикалық тұрақты).
- электростатикалық тұрақты).
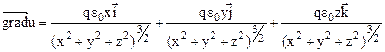 (8)
(8)
Егер 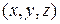 нүктесінің радиус - векторын
нүктесінің радиус - векторын 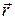 деп белгілесек, онда
деп белгілесек, онда 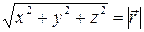 және градиентті былай жазуға болады:
және градиентті былай жазуға болады: 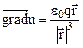 . Біз әрбір нүктедегі градиенттің осы нүктенің радиус – векторына коллинеар екенін көреміз және координаталар басынан бағытталған, оның модулі
. Біз әрбір нүктедегі градиенттің осы нүктенің радиус – векторына коллинеар екенін көреміз және координаталар басынан бағытталған, оның модулі 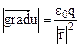 координаталар басынан қашықтықтың квадратына кері пропорционал. Мұнда біз әр нүктедегі градиенттің, осы нүктеден өтетін деңгейлік бетіне - сфераға перпендикуляр екенін көз жеткіземіз.
координаталар басынан қашықтықтың квадратына кері пропорционал. Мұнда біз әр нүктедегі градиенттің, осы нүктеден өтетін деңгейлік бетіне - сфераға перпендикуляр екенін көз жеткіземіз. 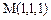 нүктедегі өрістің деңгейлік бетіне жүргізілген жанама жазықтықтың теңдеуін табайық. Деңгейлік бетінің теңдеуін табу қажет емес. (8) теңдіктен
нүктедегі өрістің деңгейлік бетіне жүргізілген жанама жазықтықтың теңдеуін табайық. Деңгейлік бетінің теңдеуін табу қажет емес. (8) теңдіктен 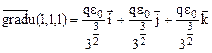 екені шығады және (6) теңдіктен
екені шығады және (6) теңдіктен
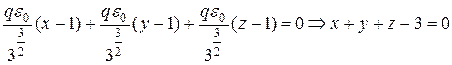 . Жазықтық радиус - векторға
. Жазықтық радиус - векторға 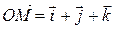 перпендикуляр екені шығады.
перпендикуляр екені шығады.
Анықтама. 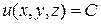 бетінің жанамасына перпендикуляр түзу
бетінің жанамасына перпендикуляр түзу 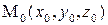 жанасу нүктесіндегі осы беттің нормалі деп атайды.
жанасу нүктесіндегі осы беттің нормалі деп атайды.
Кез келген 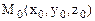 беттің регуляр нүктесінде нормаль болады және функцияның осы нүктедегі градиентінің бағытында өтеді. Оның параметрлік теңдеулерінің түрі:
беттің регуляр нүктесінде нормаль болады және функцияның осы нүктедегі градиентінің бағытында өтеді. Оның параметрлік теңдеулерінің түрі:
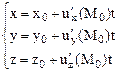 .
.
Мысал. Эллипстік параболоид 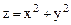 -тің
-тің 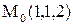 нүктесіндегі жанама жазықтығының және нормаль теңдеуін жазу керек. Бұл теңдеуді
нүктесіндегі жанама жазықтығының және нормаль теңдеуін жазу керек. Бұл теңдеуді 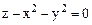 түрінде жазайық, бұл
түрінде жазайық, бұл 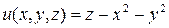 функциясының 0 деңгейлік бетін анықтайды. Осыдан
функциясының 0 деңгейлік бетін анықтайды. Осыдан 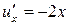 ,
, 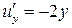 ,
, 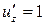 . Демек,
. Демек, 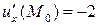 ,
, 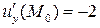 ,
, 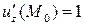 . Бұл мәндерді жанама жазықтықтың теңдеуіне қойсақ:
. Бұл мәндерді жанама жазықтықтың теңдеуіне қойсақ: 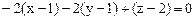 , немесе
, немесе 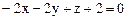 шығады. Нормаль түзудің параметрлік теңдеуі мына түрде болады:
шығады. Нормаль түзудің параметрлік теңдеуі мына түрде болады:
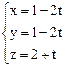 .
.
