Вимоги до логічно правильних означень понять
Розглянемо правила означень понять, які даються через рід і видову відмінність (саме такі означення переважають в шкільному курсі математики).
1. Означуване і визначальне поняття повинні бути сорозмірні.
Це означає, що сукупності об’єктів, що охоплюються ними повинні співпадати.
2. Не можна давати означення поняттю через саме себе, або через інше поняття, яке визначається через нього (це заперечення порочного кругу).
3. В означенні поняття повинні бути вказані всі властивості (ознаки), які однозначно виділяють об’єкти, що належать об’єму означуваного поняття.
4. В означенні поняття не повинно бути вказано зайвих властивостей, які випливають з інших властивостей, які також включені в означення поняття (це відсутність надмірності).
Іноді одному і тому ж поняттю даються різні означення. В такому разі вони повинні бути рівносильні, тобто з властивостей, які включені в одне означення, повинні випливати властивості, які покладені в основу іншого означення.
Наприклад: «Квадратом називається ромб, у якого всі кути прямі».
«Квадратом називається прямокутник, у якого всі сторони рівні».
5. Необхідно, щоб означуваний об’єкт існував.
Наприклад: «Прямокутним трикутником називається трикутник, у якого всі кути прямі». Такого трикутника не існує. Отже, даному означенню реально нічого не відповідає, а тому це означення логічно правильним бути не може.
Приклади математичних понять, які розглядаються в початковому курсі математики
Початковий курс математики насичений різними математичними поняттями. Починаючи з першого класу і до четвертого учні знайомляться з такими поняттями, як цифра, число, доданок, сума, зменшуване, від’ємник, різниця, множник, добуток, ділене, дільник, частка, дріб, відрізок, трикутник, многокутник, квадрат, прямокутник, коло, круг, довжина відрізка, периметр, площа, куб, маса, ємність, час, вираз, рівняння, нерівність, рівність і багато інших.
Вчитель початкових класів повинен слідкувати за правильним визначенням понять, які формує в учнів.
Питання для самоконтролю
1. Що називається висловленням? Наведіть приклади висловлень, встановіть їх значення істинності.
2. Дайте означення простих і складених висловлень, предиката. Наведіть власні приклади.
3. Що називається кон’юнкцією висловлення? Побудуйте таблицю істинності.
4. Що називається диз’юнкцією висловлення? Побудуйте таблицю істинності.
5. Дайте означення заперечення висловлення. Поясність два способи побудови заперечення висловлення, наведіть приклади.
6. Дайте означення імплікації висловлення, побудуйте таблицю істинності.
7. Що називається еквіваленцією висловлень? Побудуйте таблицю істинності, наведіть приклади висловлень, що мають структуру еквіваленції.
8. Перелічіть квантори загальності і існування, поясніть встановлення істинності і хибності висловлень з кванторами.
9. Назвіть правила побудови заперечень висловлень, що містять квантори.
10. Дайте означення теореми, назвіть її структуру. Перелічіть усі види теорем. Які з них є рівносильними?
11. Наведіть приклади найпростіших схем правильних міркувань.
12. Поясніть способи доведення геометричних тверджень.
13. Перелічіть математичні поняття. В чому їх особливість?
14. Дайте означення об’єму і змісту поняття.
15. Поясність структуру означення поняття через рід і видову відмінність. Наведіть приклади означень з курсу шкільного курсу математики, поясніть їх структуру.
Система вправ
1. Наведіть кілька тверджень (математичних і нематематичних), які є висловленнями. Позначте їх буквами А, В, С і встановіть значення їх істинності.
2. Записати інакше складені висловлення: 5≥3; (а – 1)2 ≥ 0; - 4 2 ≥ 0;
( - х)3 ≤ 0; - 5 ≥ - 1 і зробити висновок про їх істинність.
3. Записати вирази, що відповідають складеним висловленням:
А) «Ми підемо в кіно або в театр»;
Б) «Ввечері я буду читати книжку і дивитися телепередачу»;
В) «Додаткове заняття проведемо або в понеділок, або у вівторок, або у суботу».
4. Користуючись таблицею істинності, доведіть істинність або хибність висловлень:
А) X 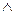 Y
Y 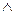 Z
Z 
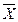
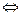 Y
Y 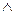
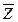 ;
;
Б) X 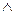 Y
Y  Z
Z 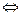
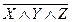 .
.
5. Подати предикат х2 – 1 = 0 у вигляді диз’юнкції двох простих предикатів і знайти множину його істинності.
6. Записати у вигляді формули такі висловлення:
А) «Якщо ціле число n ділиться на 6, то воно ділиться на 2 і на 3; ціле число n не ділиться на 2, отже, воно не ділиться на 6»;
Б) «Або А істинне, або В істинне» еквівалентне висловленню «Неправильно, що А хибне і В хибне»;
В) «Якщо з А слідує В, то з А і С слідує В і С»;
Г) «(А або В) і С еквівалентне (А або С) і (В або С)»;
Д) «Неправильно, що А і істинне, і хибне одночасно».
7. Користуючись поняттям логічного слідування, перевірити, чи є наведені нижче умовиводи логічно правильними (незалежно від їх фактичної істинності):
А) «Я сьогодні буду розв’язувати задачі або піду в похід на лижах. Я сьогодні не буду розв’язувати задачі. Отже, я сьогодні піду в похід на лижах.»;
Б) «Якщо Сашко настирливий, то він розв’яже цю задачу. Якщо у Сашка болить голова, то він не розв’яже цієї задачі. Отже, якщо у Сашка болить голова, то він не настирливий.»;
В) «Якщо викладач добре читає лекції, то студенти поважають викладача. Якщо студенти не поважають викладача, то він приймає екзамен не строго. Отже, якщо викладач приймає екзамен строго, то він добре читає лекції.»
8. Пояснити істинність (хибність) висловлень і побудувати до них заперечення:
А) «Квадрат є прямокутником»
Б) «Деякі непарні числа діляться на 13».
9.  Скласти таблицю істинності висловлень :
Скласти таблицю істинності висловлень :
А) (В 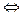
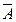 )
) 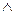
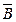 ,
,
_ ______
Б) А=>(В 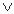 А).
А).
10. Записати за допомогою предикатів та кванторів загальності або існування:
А) теорему Піфагора (пряму і обернену);
Б) теорему про можливість описати коло навколо трикутника;
В) теорему про можливість вписати коло в чотирикутник;
Г) третю ознаку рівності трикутників (за трьома сторонами).
11. До даної теореми сформулювати пряму, обернену, протилежну і обернену до протилежної теореми:
А) «У трикутнику сума кутів дорівнює 180°»;
Б) «Діагоналі прямокутника рівні».
12. Перелічіть характеристичні ознаки фігур: паралелограм, прямокутник, квадрат, ромб. Яке відношення між їх обсягом і змістом?
13. Знайдіть і виправте помилку в таких означеннях:
А) радіусом кола називається відстань від центра кола до будь-якої її точки;
Б) вписаним кутом називається кут, вершина якого лежить на колі. Наведіть контрприклади, які спростовують таке означення.
14. Дайте означення поняттю «рівнобедрений трикутник», назвіть рід і видову відмінність.
15. Покажіть за допомогою кругів Ейлера відношення між об’ємами понять многокутник, чотирикутник, паралелограм, прямокутник, квадрат, ромб.
Розділ ІІ
