Параметры трех состояний газа представлены в таблице

ЛАБОРАТОРНАЯ РАБОТА № 1

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ Ср/Сv

Определение отношения теплоемкостей воздуха С_р/С_v методом адиабатического расширения.

Оборудование: толстостенный стеклянный сосуд, жидкостный манометр, насос Шинца, трехходовой кран.

Сущность метода: определение g = С_р/С_v основано на адиабатическом расширении газа.

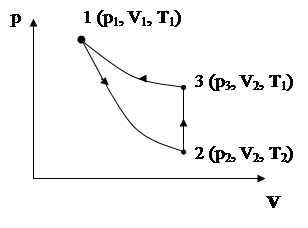В баллон насосом подкачивают воздух, создавая давление выше атмосферного. Газ характеризуется параметрами V₁, Р₁, Т₁ (на графике точка 1). Быстро открыв и закрыв кран, соединяющий баллон с окружающей средой, получим адиабатическое расширение воздуха. Газ перейдет в новое состояние, характеризуемое параметрами V₂, Р₂, Т₂ (на графике точка 2). Причем Т₂>Т₁ .Через несколько минут газ нагреется до температуры окружающего воздуха (Т₁), при этом при V₂ = соnst давление повысится до Р₃. Новое состояние газа будет характеризоваться параметрами Р₃, V₂, Т₁ (на графике точка 3).

Параметры трех состояний газа представлены в таблице

Порядковый номер состояния газа	Условия опыта	Объем	Давление	Температура
	До открытия крана	V1	P1 = P2 + h1	T1
	В момент открытия крана	V2	P2	T2
	После закрытия крана	V2	P3 = P2 + h2	T1

Можно сравнивать начальное (1) и конечное (2) состояния газа и использовать закон Бойля и Мариотта, или можно сравнивать 2 и 3 состояния газа при V₂ -соnst и использовать закон Шарля:

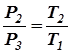
К процессу перехода газа из 1 состояния во 2 (адиабатическое расширение) применимо уравнение адиабаты (закон Пуассона)

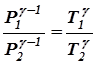
В ходе эксперимента необходимо измерить разность уровней жидкости в манометре.

В первом состоянии:

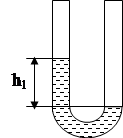h₁ - разность уровней до расширения воздуха.

Р₁ = Р₂ + h₁ ,

где Р₂ - атмосферное давление.

В третьем состоянии:

h₂ - разность уровней после расширения воздуха.

Р₃ = Р₂ + h₂ ; h₂ = Р₃ - Р₂

Получим расчетную формулу:

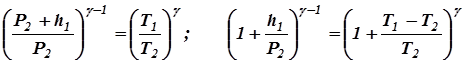
Разложим данные выражения по биному Ньютона и ограничимся членами первого порядка

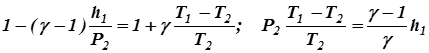
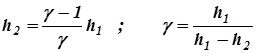
Задание 1

1. Трехходовой кран устанавливают так, чтобы баллон соединялся с насосом и манометром, а доступ с атмосферой был перекрыт. Осторожно накачивают воздух, чтобы разность уровней жидкости в манометре составлял не менее 20 см.

2. Закрывают кран так, чтобы, перекрыв связь с насосом, баллон был соединен только с манометром, и через 2-3 минуты после прекращения изменения уровней жидкости отсчитывают h₁.

3. Резко открывают и закрывают кран, соединяющий баллон с атмосферой. Через 2-3 минуты после прекращения изменения уровней жидкости в манометре отсчитывают h₂.

4. Проделывают не менее 10 измерений.

5. Рассчитывают ошибку результатов измерений

№, п/п	h1, м	h2, м	g	gСР	Dg	DgСР	e, %

Можно ли обосновать правильность полученного экспериментального результата ?

Проведем теоретический расчет g.

Удельной теплоемкостью с называется теплоемкость единицы массы однородного вещества.

,

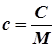где С - теплоемкость,

М - масса тела.

Если теплоемкость относят к одному молю (m/m) вещества, то ее называют молярной.

Теплоемкостью С тела называется отношение элементарного количества теплоты Q , сообщенного телу в каком-либо процессе к соответствующему изменению температуры тела:

.

Теплоемкость зависит от массы тела, его химического состава, термодинамического состояния и вида процесса сообщения теплоты.

Проведем рассуждения для одного моля газа.

Газ можно нагревать при постоянном объеме (молярная теплоемкость при постоянном объеме С_V ) или при постоянном давлении (молярная теплоемкость при постоянном давлении С_P). Воспользуемся первым законом термодинамики:

DQ = DU + А

1) При нагревании газа при V = соnst все количество теплоты идет только на увеличение внутренней энергии газа

DQ = DU ; С_V ×DТ = DU ; С_V = DU / D Т

2) При нагревании газа при Р = соnst , кроме теплоты, идущей на повышение внутренней энергии газа, необходимо еще тепло для совершения работы расширения газа ( А = Р×DV ).

С_P×DТ = DU + Р×DV = DU + R×DТ

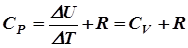- ( уравнение Майера )

Исходя из представления молекулярно-кинетической теории газов внутренняя энергия одного моля газа распределяется в среднем поровну между всеми степенями свободы молекулы 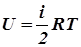, тогда молярная теплоемкость при постоянном объеме будет равна, 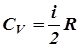, а молярная теплоемкость при постоянном давлении

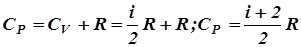
Одноатомному газу приписывают 3 (i = 3) степени свободы, двухатомному - 5 (i = 5), а многоатомному (например, воздух) - 6.

Тогда: g = C_P / C_V = 7 / 5 = 1,40

Дополнительные сведения к методике эксперимента по способу Клемана и Дезорма.

1. В начале в сосуде давление воздуха соответствовало атмосферному давлению. В результате накачивания небольшой порции воздуха давление увеличивается. Так как, сжатие воздуха адиабатическое, то его температура повысилась. Разность уровней в манометре (h₁) установится только тогда, когда в результате теплопроводности стеклянных стенок сосуда температура воздуха в сосуде сравняется с температурой окружающего воздуха. Поэтому, после нагнетания воздуха необходимо подождать пока установится постоянная разность высот h₁.

Параметры первого состояния: Р₁ = Р₂ + h₁ ; V₁ ; Т₁ .

2. Следующим этапом эксперимента является быстрое открытие крана. При этом воздух начнет адиабатически расширяться, пока давление его не станет равным атмосферному. Газ совершает работу за счет изменения его внутренней энергии (воспользуйтесь первым законом термодинамики, определением адиабатического процесса и объясните данный факт), поэтому температура воздуха понижается до Т_2.

Параметры второго состояния: Р₂ ; V₂ ; Т₂ , причем V₂ > V₁, т.к. масса m занимает весь объем сосуда.

3. Закрываем кран. Давление возрастает, потому что воздух в сосуде начинает нагреваться за счет притока тепла извне. Когда Т₂ = Т₁, рост давления прекращается.

Параметры третьего состояния: Р₃ = Р₂ + h₂ ; V₂ ; Т₁.

2 способ. Определение g по скорости звука в газе.

Оборудование: осциллограф, трубка (ℓ = 0,63 м) с телефонами, звуковой генератор, барометр-анероид, жидкостный термометр.

Сущность метода: В трубке с воздухом возбуждаются колебания звуковой частоты. Амплитуда колебаний будет максимальной, если добиться наступления акустического резонанса. Резонанс наступит, когда в трубке будет укладываться целое число полуволн бегущей звуковой волны или целое число длин волн стоячих звуковых волн.

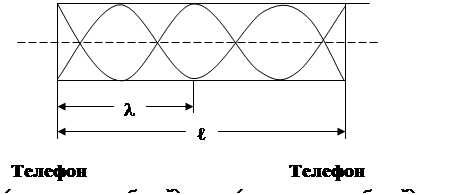ℓ = (l / 2)×n

n - число длин полуволн

Получим расчетную формулу:

Скорость звука, плотность газа и его давление связаны соотношением:

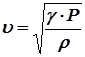, где g = С_P / C_V

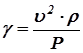
1) Плотность воздуха определим из уравнения Менделеева-Клапейрона

m = 29×10^-3 кг/моль ; R = 8,31 Дж/(моль×К)

2) Давление определим по показаниям барометра-анероида.

3) u=l×n ; u=(2ℓ×n) / n

Число n определим из двух последовательных резонансных состояний системы, при которых устанавливаются стоячие волны.

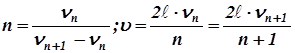
Тогда отношение С_P/С_V будет равно:

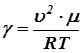
Добейтесь на экране осциллографа колебаний достаточной амплитуды. Плавно изменяя частоту подаваемого сигнала, по всплескам амплитуды колебаний на экране, зафиксируйте моменты наступления резонанса. Запишите резонансные частоты и для каждой подсчитайте скорость звука.

Рассчитайте ошибку результата измерения и сравните значения отношения С_P/С_V , полученные разными способами.

ВОПРОСЫ.

Что называют внутренней энергией? Количеством теплоты?

Определение и математическое выражение теплоемкости тела, удельной теплоемкости вещества, молярной теплоемкости вещества.

Почему для газов различают теплоемкость при постоянном объеме (С_V) и теплоемкость при постоянном давлении (С_Р) ?

Дать определение молярных теплоемкостей при постоянном объеме и постоянном давлении, объяснить соотношение между ними (уравнение Майера).

Дать понятие о степени свободы; выразить С_Р и С_V через число степеней свободы.

Адиабатный процесс. Уравнение Пуассона, график адиабатного процесса.

Определение С_Р / С_V методом адиабатного расширения (ход работы).

Что называется волной? Как образуется стоячая волна, ее особенности.

Что называется длиной волны?

Что такое резонанс? Условие наступления резонанса в трубе с воздухом.

Что называется скоростью звука? Плотностью (газа), давлением? Соотношение между ними.

Вывод расчетной формулы для g. Методика эксперимента по определению g.