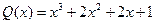Найбільший спільний дільник та найменше спільне кратне многочленів.
Підготував: проф. Петрівський Б.П.
Рівне - 2010
Рівняння 3-го і 4-го степенів та їх розв’язання методом Кардано та Феррарі.
Розглянемо рівняння 3-го степеня: 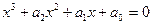 в полі с.
в полі с.
Покажемо що за допомогою заміни 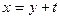 можна позбутися квадрата невідомої величини. Справді:
можна позбутися квадрата невідомої величини. Справді:
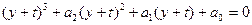 або
або
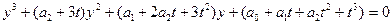 . Підбедемо t так, щоб
. Підбедемо t так, щоб 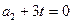 , тобто
, тобто 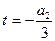 , тоді одержимо:
, тоді одержимо:
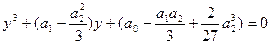 .
.
Рівняння 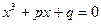 (1) називається зведеним кубічним рівнянням.
(1) називається зведеним кубічним рівнянням.
Будемо шукати розв’язок цього рівняння у виді 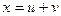 .
.
Отримаємо: 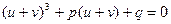 або
або 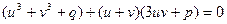 . Покладемо (2)
. Покладемо (2) 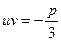 , тоді
, тоді 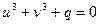 . Тобто (3)
. Тобто (3) 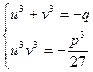
Позначимо: 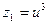 ,
, 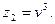 Згідно теореми Вієта
Згідно теореми Вієта 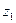 і
і 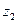 є розв’язками рівняння:
є розв’язками рівняння:
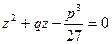 звідси
звідси 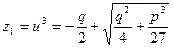
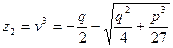 звідси
звідси 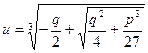 ,
, 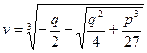
і 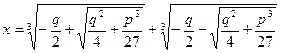 (4) – формула Кардано.
(4) – формула Кардано.
Оскільки корінь третього степеня з комплексного числа має три різні комплексні значення, то з формули (4) отримаємо дев’ять комплексних чисел. Цей результат є наслідком того, що 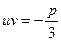 не є еквівалентним
не є еквівалентним 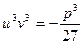 .
.
На практиці ми знаходимо три значення u з формули 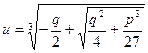 , а відповідні значення v знаходимо з умови (2)
, а відповідні значення v знаходимо з умови (2) 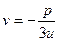 . Іноді краще знаходити значення v, а відповідні значення u знаходимо з формули (2).
. Іноді краще знаходити значення v, а відповідні значення u знаходимо з формули (2).
Приклад. Розв’язати рівняння: 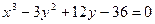 .
.
Розв’язання:
Нехай 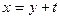 . Одержимо
. Одержимо 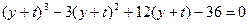 або
або
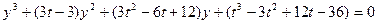
Якщо 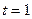 , то
, то 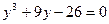 .
.
Розв’яжемо 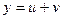 , тоді
, тоді 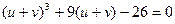 або
або
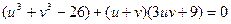 . Виберемо u та v так, щоб
. Виберемо u та v так, щоб 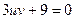 або
або 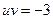 , тоді
, тоді 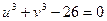 . Маємо
. Маємо 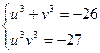
Позначимо: 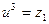 ,
, 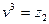 . Тоді маємо рівняння
. Тоді маємо рівняння 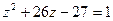
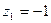 ,
, 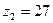 .
.
Звідси 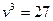 ,
, 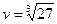 ,
, 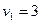 ,
, 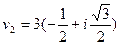 ,
, 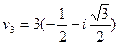 .
.
Знайдемо відповідні значення 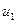 ,
, 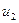 ,
, 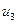 .
.
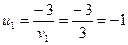 ;
;
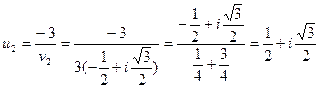 ;
;
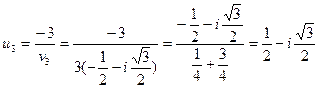 .
.
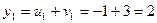 ;
;
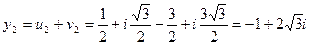 ;
;
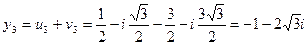 .
.
Значить, 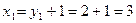 ;
; 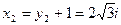 ;
; 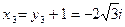 .
.
Розглянемо метод Феррарі розв’язування рівняння: 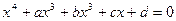 (5)
(5)
Виділимо з перших двох доданків квадрат:
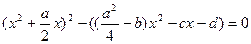 .
.
1. Нехай 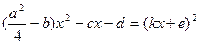 , тоді
, тоді 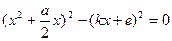 або
або
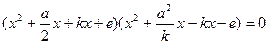 і розв’язок рівняння
і розв’язок рівняння
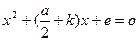 та
та 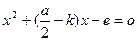 будуть розв’язками рівняння (5).
будуть розв’язками рівняння (5).
2. Якщо 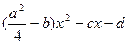 не є квадратом, то вводимо параметр
не є квадратом, то вводимо параметр 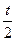 так, щоб цей вираз був квадратом (6)
так, щоб цей вираз був квадратом (6) 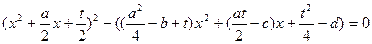 .
.
Підберемо 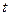 так, щоб вираз другого доданку був квадратом (для цього дискримінант квадратного тричлена дорівнює 0).
так, щоб вираз другого доданку був квадратом (для цього дискримінант квадратного тричлена дорівнює 0).
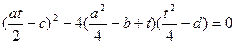 або
або
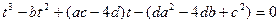 (7)
(7)
Рівняння (6) називається резольвентним (розв’язуючим рівнянням) рівнянням для (5).
Знайшовши будь-який розв’язок 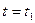 рівняння (7) та підставивши його значення в (6), отримаємо:
рівняння (7) та підставивши його значення в (6), отримаємо:
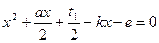 та
та 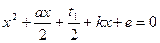 .
.
Розв’язки цих рівнянь будуть розв’язками рівняння (5). На практиці замість параметра 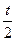 часто розглядають параметр
часто розглядають параметр 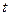 .
.
Приклад 2. Розв’язати рівняння: 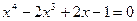 .
.
Розв’язання:
Виділимо квадрат: 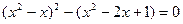 або
або 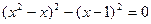 .
.
Звідси 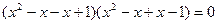 або
або 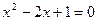 ,
, 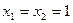
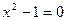 ,
, 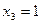 ,
, 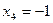 .
.
Приклад 3. Розв’язати рівняння: 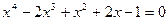 .
.
Розв’язання:
Маємо 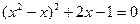 , введемо параметр
, введемо параметр 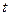 :
:
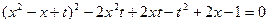 або
або
(8) 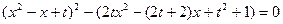
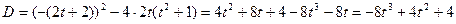 . Резольвентним рівнянням буде:
. Резольвентним рівнянням буде: 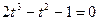 . Одним з розв’язків цього рівняння буде
. Одним з розв’язків цього рівняння буде 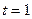 . Підставимо
. Підставимо 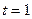 в (8)
в (8)
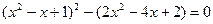 або
або 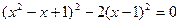
Звідси 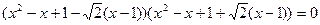
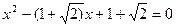
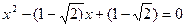
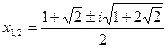
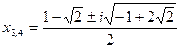
Розв’язати методом Кардано рівняння:
1. 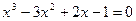
2. 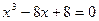
3. 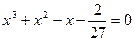
4. 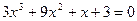
5. 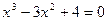
6. 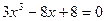
7. 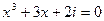
8. 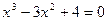
9. 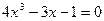
10. 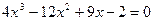
11. 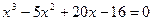
12. 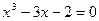
13. 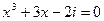
14. 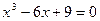
15. 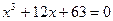
16. 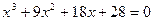
17. 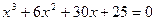
18. 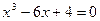
19. 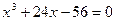
20. 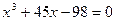
21. 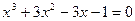
22. 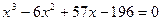
23. 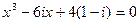
24. 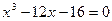
25. 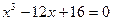
26. 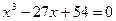
27. 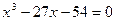
28. 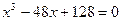
29. 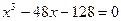
30. 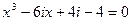
Розв’язати рівняння методом Феррарі:
1. 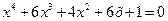

2. 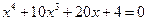
3. 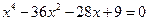
4. 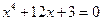
5. 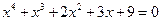
6. 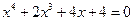
7. 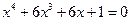
8. 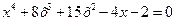
9. 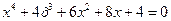
10. 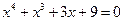
11. 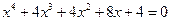
12. 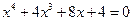
13. 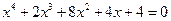
14. 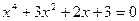
15. 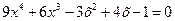
16. 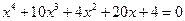
17. 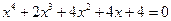
18. 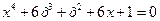
19. 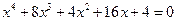
20. 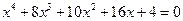
21. 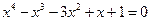
22. 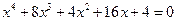
23. 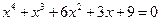
24. 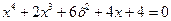
25. 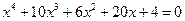
26. 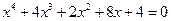
27. 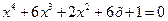
28. 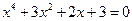
29. 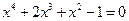
30. 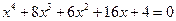
Найбільший спільний дільник та найменше спільне кратне многочленів.
Розглянемо многочлени  та
та  над полем П.
над полем П.
Спільним дільником многочленів  та
та  називається многочлен
називається многочлен 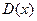 на який діляться без остачі ці многочлени.
на який діляться без остачі ці многочлени.
Найбільшим спільним дільником многочленів  та
та  називається спільний дільник, який ділиться без остачі на будь-який інший спільний дільник.
називається спільний дільник, який ділиться без остачі на будь-який інший спільний дільник.
Алгоритмом Евкліда для многочленів  та
та  є така сукупність рівностей (
є така сукупність рівностей ( 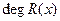 - степінь многочлена
- степінь многочлена 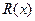 :
:
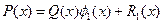 ,
, 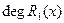 <
< 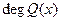
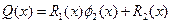 ,
, 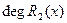 <
< 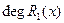
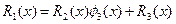 ,
, 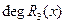 <
< 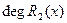
… …
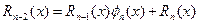 ,
, 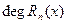 <
< 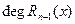
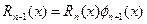
Теорема Евкліда: Остання відмінна від нуль-многочлена остача алгоритму дорівнює найбільшому спільному дільнику.
Якщо многочлен  ділиться на многочлен
ділиться на многочлен  , то для будь-якого сталого
, то для будь-якого сталого 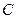
 ділиться й на
ділиться й на 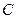
 . Значить алгоритм Евкліда можна застосувати з точністю до сталого множника.
. Значить алгоритм Евкліда можна застосувати з точністю до сталого множника.
Приклад 1. Знайти за алгоритмом Евкліда найбільший спільний дільник многочленів 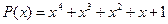 та
та 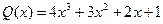 . Щоб уникнути дробових коефіцієнтів будемо при потребі домножати (ділити ) многочлени чи остачі при діленні на сталі числа. Зрозуміло, що при цьому частки зміняться, але той факт ніяк не впливає на знаходження
. Щоб уникнути дробових коефіцієнтів будемо при потребі домножати (ділити ) многочлени чи остачі при діленні на сталі числа. Зрозуміло, що при цьому частки зміняться, але той факт ніяк не впливає на знаходження 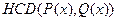 ,
,

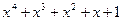
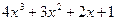
 (множимо на 4)
(множимо на 4) 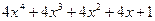
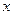




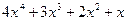


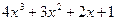
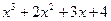
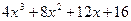
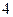
(ділимо на -5) 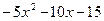

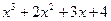
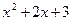

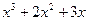
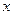
(ділимо на 4) 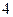


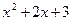

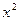
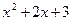
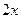


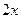




 .
.
Отже, остання відмінна від нуль-многочлена остача дорівнює 1. 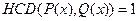
Як відомо, для будь-яких многочленів  і
і  існують такі многочлени
існують такі многочлени 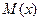 та
та 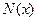 , що виконується тотожність
, що виконується тотожність 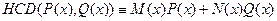 .
.
Для знаходження 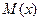 ,
, 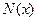 потрібно застосувати алгоритм Евкліда, але при цьому не можна домножати (ділити) на сталі числа.
потрібно застосувати алгоритм Евкліда, але при цьому не можна домножати (ділити) на сталі числа.
Знайти 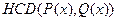 та
та 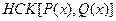 , якщо:
, якщо:
1. 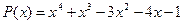 ,
, 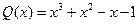
2. 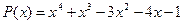 ,
, 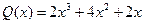
3. 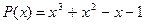 ,
, 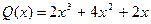
4. 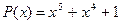 ,
, 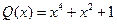
5. 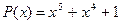 ,
, 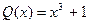
6. 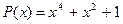 ,
, 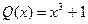
7. 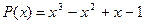 ,
, 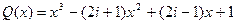
8. 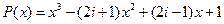 ,
, 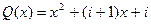
9. 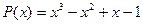 ,
, 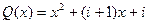
10. 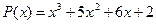 ,
, 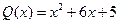
11. 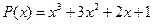 ,
, 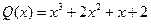
12. 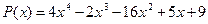 ,
, 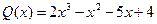
13. 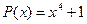 ,
, 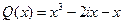
14. 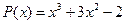 ,
, 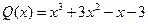
15. 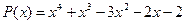 ,
, 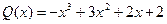
16. 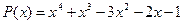 ,
, 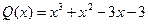
17. 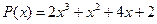 ,
, 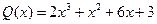
18. 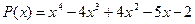 ,
, 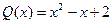
19. 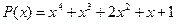 ,
, 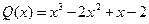
20. 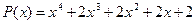 ,
, 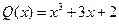
21. 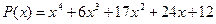 ,
, 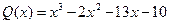
22. 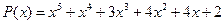 ,
, 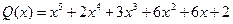
23. 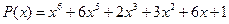 ,
, 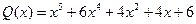
24. 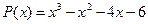 ,
, 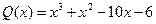
25. 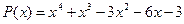 ,
, 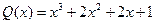
26. 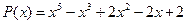 ,
, 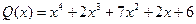
27. 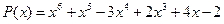 ,
, 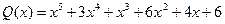
28. 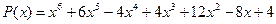 ,
, 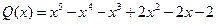
29. 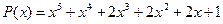 ,
, 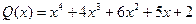
30. 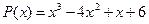 ,
,