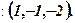До задачі 1

Вказівки до розв’язування задач

Типового варіанту

До задачі 1

Варіант 0: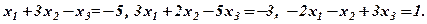

Розв’язання. а) Позначимо рівняння системи:

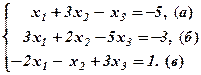
Вписуємо елементи системи в обчислювальну таблицю (див. 1.1, табл.1, або приклад 1, табл.2)

N п/п	X1	X2	X3	Вільни члені	Суми	Контроль
			-1	-5	-2
			-5	-3	-3
	-2	-1
		-7	-2
				-9	-3	-3

Зворотний хід. Виписуємо трикутну систему згідно з рядками1, 4, 6, куди входять провідні елементи

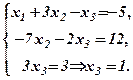
З другого рівняння трикутної системи

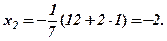
З першего рівняння

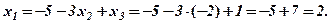
Відповідь: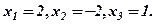

б) Обчислимо визначники: 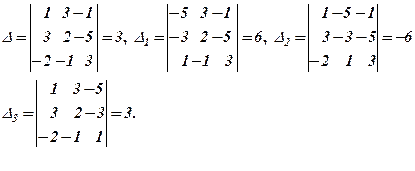За формулами Крамера: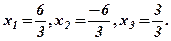

в) Позначення А — матриця системи, В — стовпець вільних членів, Х — стовпець невідомих:

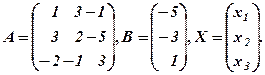
Матричний вигляд системи: АХ=В. Розв’язання цього рівняння (за умови існування оберненої матриці А^-1):

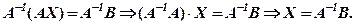
Формула оберненої матриці:

якщ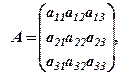о то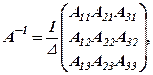

де D ¹ 0 - визначник матриці А; А_ij — алгебраїчне доповнення до елементу а_ij матриці А.

У цій задачі D = 3 Þ А^-1існує. Обчислюємо А_ij:

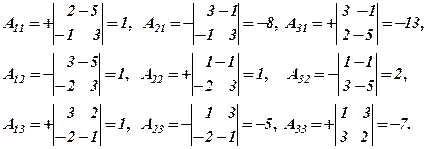
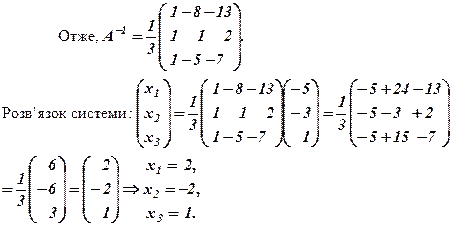
До задачі 2

Варіант 0: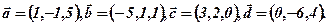

Відповіді і вказівки.

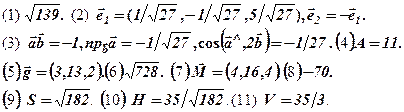
(12)Використати скалярний добуток векторів (умову ортогональності). Відповідь: t =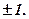

(13)Три вектори утворюють базис тільки тоді, коли визначник, складений з кординат цих векторів, відмінний від 0:

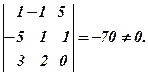
Нехай 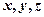- координати 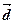у новому базисі: .

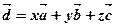Виконуючи дії з координатами, перепишемо цю рівність у координатному вигляді: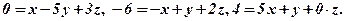

Розв’язок системи:

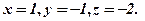Відповідь