Беттің жанама жазықтығы

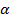жазықтығы Ф бетінің Р нүктесінен өтетін болсын. Беттің үстінен Q нүктесін алып, одан Р нүктесіне және 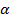жазықтығына дейінгі қашықтықтарды d және h деп белгілейік(30-сурет).

Егер ұмтылғанда , онда 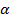жазықтығы Р нүктесінде бетке жанама жазықтық деп аталады.

Теорема. Тегіс Ф беттің әрбір нүктесінде жалғыз ғана жанама жазықтығы ьолады. Егер беттің тегіс параметризациясы болса, онда нүктесіндегі жанама жазықтық векторларына параллель.

Дәлелдеуі. нүктесіндегі Ф бетіне жанама жазықтық 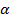болсын және оның бірлік нормаль векторы 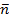болсын. нүктесінен нүктесіне шейінгі қашықтық -ке тең.

.

Анықтама бойынша,

Дербес жағдайда,

егер

Бірақ

Сонымен

(себебі, ) болғандықтан,

Осы сияқты екендігін де көрсету оңай. Сонымен, егер жанама жазықтық бар болса, ол векторларына параллель екен.

Енді жанама жазықтықтың бар болатындығын көрсетелік. 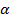жазықтығы векторларына параллель болсын, оның нүктесіндегі жанама жазықтық болатындығын көрсетелік.

Орындалатындығын көреміз. Мұндағы ұмтылғанда, және нольге ұмтылады. ұмтылғанда екенін көрсету үшін, кез-келген үшін

болатындығын дәлелдеу жеткілікті (мұндағы с-тұрақты). және сандарының квадраттарының қосындысы бірге тең болғандықтан, олардың ең болмағанда біреуі санынан кем емес. Мысалы, делік. және векторларының арасындағы бұрышты –деп, ал -ге перпендикуляр және векторларымен компланар бірлік векторды -деп белгілеп, төмендегі теңсіздіктерді аламыз.

Сол сияқты дегенмен

теңсіздігін аламыз. Сонымен тұрақты с

үшін сандарының кішісін алсақ болғаны.

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:

№ 15 лекция Квадраттық форма. (1с)

Лекция жоспары

1. Геодезиялык үшбұрыштың дефектiсi

2. Иiлiмi терiс тұракты беттер Лобачевскйдiң кiшi геометриясын өрнектеу.

Дәріс тезисі

Квадраттық форма – дәрежесі 2-ге тең x1, x2, ..., xn n айнымалыдан тұратын форма, яғни әр мүшесі не осы айнымалылардың біреуінің квадратынан не әр түрлі екі айнымалының көбейтіндісінен тұратын көпмүше. n=2 болғанда квадраттық форманың жалпы түрі мынадай: , мұндағы a, b, c – қандай да бір сандар. Кез келген квадраттық форма былайша жазылады: , мұндағы aіj – нақты сандар, ал aіj=ajі деп қарастырылады. 2, 3 және 4 айнымалыдан тұратын квадраттық формалар 2-ретті сызықтар (жазықтықта) мен беттер (кеңістікте) теориясына тікелей байланысты болып келеді. Декарттық координаттар жүйесінде центрге келтірілген 2-ретті сызықтар мен беттердің теңдеулері мына түрде жазылады: A(x)=1, яғни теңдеудің сол жағы квадраттық форма болады. Егер x1, x2, ..., xn айнымалыларын олардың сызықтық комбинациялары болатын басқа y1, y2, ..., yn айнымалыларымен алмастырсақ, онда квадраттық форма басқа квадраттық формаға ауысады. Квадраттық форманы жаңа айнымалыларды сәйкес түрде таңдап алу жолымен, белгілі санға көбейтілген осы айнымалылардың квадраттарының қосындысы түріне келтіруге болады. Бұл жағдайда, не квадраттардың саны (квадраттық форманың рангісі), не квадраттардың оң және теріс коэффициенттерінің айырмасы (квадраттық форма-ның сигнатурасы) квадраттық форманы квадраттар қосындысына келтіру тәсіліне (инерция заңы) тәуелді болмайды. Көрсетілген формаға арнаулы түрлендіру (ортогональ түрлендіру деп аталатын) арқылы келтіруге болады. Геометриялық тұрғыдан мұндай түрлендіру 2-ретті сызықты не бетті басты осьтерге келтіруге сәйкес келеді.Омар Хайям - парсы математигі, астрономы, ақын, философы (толық аты — Абу-ль-Фатх Омар ибн Ибрахим аль-Хайям) шамамен 1048 жылы Хорасанның Нишапур қаласында дүниеге келген, әрі сонда қайтыс болған. Жас кезінде жақсы отбасының тәрбиесінде болған, әрі өлеңге құмартып өскен, оның кейбір өлеңдері осы күнге дейін жеткен. Нишапурда жүмыс атқарған кезінде, сол кездегі оқымыстылармен бірлесіп сол замандағы күнтізбеге өзгерістер енгізген.Оның ең негізгі еңбегі «Алгебра мәселелерінің дәлелі» атты кітап. Бұл кітаптың арабша қолжазбасы мен латынша аударма нұсқасы сақталған, әрі қазір көптеген шет тілдеріне аударлып басылды. Осы кітапта алгебраға "теңдеу шешетін ғылым" деген анықтама берген, бұл анықтама 19-ғасырдың соңына дейін сақталып келді. Кітапта тағыда тұңғыш рет өзі ашқан көнуыстық қисықтардың көмегімен үшінші дәрежелі теңдеуді шешудің әдісі берілді, бұл алгебра мен геометрияны біріктрген керемет әдіс еді. Ол тағыда екімұшеліктердің жаймасын, тарқату әдісін да зеріттеген. Евклидтің кітабын аударып және оған түініктеме берген. Оның «Еуклидтің геометрияның бастамалары кітабындағы қиын формулаларға түсініктеме» атты кітабы шығыс математикасының дамуына ерекше рөл атқарған.Әкесі Ибраһим лашық үй жасаумен шұғылданған, “һайям” – осы кәсіпке байланысты туған атау. Ғұмыры Балх, Самарқанд, Мерв, Исфаһан, т.б. қалаларда өткен. Әйгілі ғұламалардан дәріс алып, Аристотель мен ибн Синаның философиялық көзқарастарын қолдаған. Араб, парсы тілдерін қатар меңгерген ол “Болмыс және борыш туралы трактат” (1080), “Үш сауалға жауап”, “Жалпы ғылыми пән туралы ақылдың нұры”, “Өмір сүру туралы трактат” (1980 – 91), “Наурызнама” (1095 – 98), “Өмір сүрудің жалпылық қасиеті туралы трактат” (1105 – 10), т.б. философиялық еңбектер жазды. Салжұқ сұлтанының тапсыруымен күнтізбеге реформа жасады. Бұл күнтізбе бойынша әрбір 33 жылда 8 кібісе 7 рет 4 жыл сайын, 1 рет 5 жылдан кейін болады. Мұндағы уақыт айырмасы 5000 жылда 1 тәулікке теңеледі. Оның жыл санауы Григорий күнтізбесінен анағұрлым дәл. Омар Һайям еңбектерінің басым бөлігі математика ғылымының үлесінде. “Алгебра және әлмұқабала мәселелерін дәлелдеу туралы” трактатында математикалық тарихында тұңғыш рет үшінші дәрежелі теңдеулерді саралап, оларды шешудің жүйесін жасауға талпынды, куб теңдеулердің әр түрінің (барлығы 19) түбірін геометриялық тәсілмен шешуді ұсынды. Үш кітаптан тұратын “Евклид еңбектеріндегі қиын тұжырымдарға түсініктеме” зерттеуінің “Параллель түзулердің шын мәні туралы” деп аталатын бірінші кітабында Евклид ұғымына дәл келетін параллель түзулердің жаңа теориясы баяндалған. “Қатынастар, пропорциялар және олардың нақтылы мәні туралы” атты екінші кітабында Евклидтің қатынастар теориясын жетілдіріп, сандар мен шамаларға ортақ теория жасауға күш салды. “Қатынастарды құру және оларды зерттеу” туралы кітабында шамалардың рационал және иррационал қатынастарына сандық өрнек табу жөніндегі Әбу Наср әл-Фараби идеясын дамытып, сан ұғымын оң нақты сан ұғымына дейін кеңейту қажеттігін дәлелдеді. Омар Һайям еңбектеріндегі жаңалықтарды Әбу Жафар ат-Туси, т.б. математиктер дамытты. “Дене құрамындағы алтын мен күмістің мөлшерін анықтау тәсілі туралы” трактатында Архимед шешкен физикалық есептерді жетілдірді. Омар Һайям медицина, музыкалық теориясымен де шұғылданды.Омар Һайям әлемге аян төрт тағандардың (рубай) авторы. Өлеңдерін парсы тілінде жазды, оның ақындығын алғаш таныған (1176) ғалым Байхаки еді. Ақын өмір мен өлім, жақсы мен жаман, жұмақ пен тозақ, қанағат пен обырлық, жастық пен кәрілік, махаббат пен зұлымдық, құштарлық пен тақуалық парқын төрт жолдан тұратын өлеңге сыйғызды. Оның рубайлары адамгершілік ұстанымдарға негізделген, ол әділетсіздікке қарсылық білдірді, қоршаған ортаға сын көзімен қарап, озық ойларын батыл айта білді. Өз ойын жеткізу үшін белгілі дәрежеде бейнелеу тәсілдерін қолданды. Мысалы, құмыра, пияла, дүкен, шеберхананы жырлау арқылы жаратушы мен әлемнің, адамның арақатынасын сипаттаса, адам мүрдесі топыраққа айналған жерден өсіп шыққан гүлді өмір мен материяның мәңгілік құбылысы ретінде бейнеледі. Ақын өлеңдерінде махаббатты жырлау арқылы метафоралық терең ой тұжырымдалды. Оның өлеңдерінен ақиқатқа талпыныс, тіршіліктің мәнін парықтау мен енжарлықты, екіжүзділікті әжуәлау сарыны байқалады. Омар Һайям өлеңдері аз сөзбен келелі ой айтуымен, қарапайым сөздердің өзара жарасымды үйлесім тауып, әуезді болып келуімен ерекшеленді. 19 ғасырда Э.Фицджеральд ақын өлеңдерін ағылшын тіліне аударды (1859). Бұл аударманы ғалым Теннисон “жаңадан ашылған планетаға” теңесе, кей ғалымдар тақырып әуендерін өзінше өзгертіп, кейде қосымшалар енгізіп жіберген деген пікір айтады (Идрис Шах “Суфизм”, М., 1994, 193 – 201-б.). Омар Һайям рубайларының І.Шаңғытбаев аударған нұсқасы (325 рубай) 1965 жылы жеке кітап болып шықты. Ө.Күмісбаев “Иранбақтың бұлбұлдары” атты жинағында бірнеше шығыс ақындарымен қатар Омар Һайям өлеңдерін аударды (2004). Омар Һайямның кесенесі Нишапур қаласында орналасқан.

НЕГІЗГІ ӘДЕБИЕТТЕР.

1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:

2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с

3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:

ҚОСЫМША ӘДЕБИЕТТЕР

1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.

2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7

3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.

4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с: