Через точку А провести фронтальную прямую f, так, чтобы она пересекала прямую а. Провести прямую b, параллельную прямой линии а.
Алгоритм решения.
1. Выделить признаки, характеризующие понятие «фронтальная прямая» и «прямые пересекающиеся».Определить алгоритм построения комплексного чертежа фронтальной прямой, пересекающей прямую линию а в точке 1.
2. Выделить признаки, характеризующие понятие «параллельные прямые». Выполнить необходимые построения (табл. 4.4).
Таблица 4.4
Геометрические построения в задаче 3
| Словесная форма | Графическая форма |
| 1. Через точку А1 провести f1 параллельно оси Oх, f1II ох. Получаем точку 11, f1∩a1=11. | 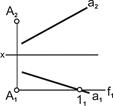 |
| 2. Поднять перпендикуляр линии связи вверх, до пересечения с a2. Получим точку 12 3. Соединить точки A2 и 12. Получим f2 | 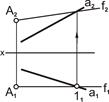 |
| 4. Построить b1 параллельно a1 и b2 параллельно a2. Получим [b1]ll[a1] и [b2]ll[a2] Þblla | 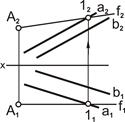 |
& Рекомендуемый библиографический список [2–11].
5. КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПЛОСКОСТИ
Задание плоскости на комплексном чертеже
Плоскостьопределяетсятремя своими точками, каждая из которых может быть задана двумя проекциями. Следовательно, на комплексном чертеже плоскость может определяться проекциями своих точек, не лежащих на одной прямой. Рассмотрим варианты задания плоскости:
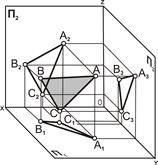
1) тремя точками, не лежащими на прямой (рис. 5.1);
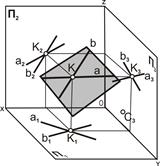
2) двумя пересекающимися прямыми (рис. 5.2);
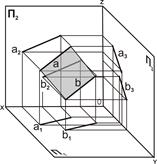
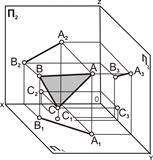
3) двумя параллельными прямыми (рис. 5.3);
4) прямой и точкой вне прямой (рис. 5.4);
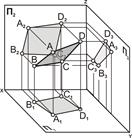
5) плоской фигурой (рис. 5.5);
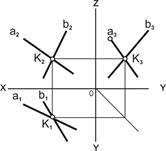
6) следом (рис. 5.6).
Примечание. Каждый последующий способ задания плоскости может быть получен из предыдущего.
 |
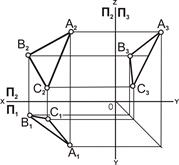 | ||||
| Рис. 5.1. Плоскость задана проекциями трех точек A, B, C: а – наглядное изображение; б – комплексный чертёж | |||||
 |
 | ||||
| Рис. 5.2 Плоскость задана проекциями двух пересекающихся прямых a и b: а – наглядное изображение; б – комплексный чертеж | |||||
 |
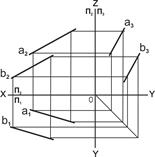 | ||||
| Рис. 5.3. Плоскость задана проекциями двух параллельных прямых a и b: а – наглядное изображение; б – комплексный чертёж | |||||
 |
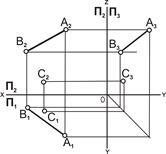 | ||||
| Рис. 5.4. Плоскость задана проекциями прямой линии AB и точки C: а – наглядное изображение; б – комплексный чертёж | |||||
 |
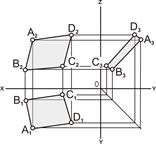 | ||||
| Рис. 5.5. Плоскость задана проекциями плоской фигуры ABCD: а – наглядное изображение; б – комплексный чертёж | |||||
 |
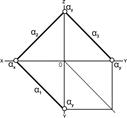 | ||||
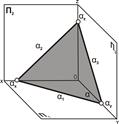
Рис. 5.6. Плоскость задана следами  1, 1, 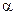 2, 2, 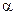 3: а – наглядное бражение; б – комплексный чертёж 3: а – наглядное бражение; б – комплексный чертёж |
Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает плоскость a, различают горизонтальный след a1, фронтальный след a2 и профильный след a3. Следы плоскости общего положения пересекаются попарно на осях в точках ax,ay,az. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций (рис. 5.6). Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
