Способы вычисления определителей

Единичная и обратная матрица (определение)

Получение обратной матрицы

Обратная матрица. Вычисление обратной матрицы.

Обратную матрицу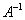можно найти по следующей формуле:

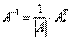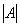, где – определитель матрицы 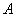, 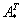– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

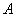Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как Вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом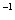

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

Пример:

Найти обратную матрицу для матрицы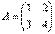

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.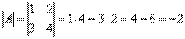

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

В рассматриваемом примере, как выяснилось, 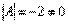, а значит, всё в порядке.

2) Находим матрицу миноров

Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .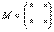
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице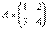
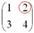
Сначала рассмотрим левый верхний элемент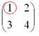

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

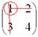
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:

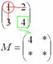
Рассматриваем следующий элемент матрицы :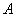

Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: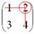

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: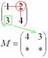

Аналогично рассматриваем элементы второй строки и находим их миноры:


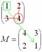
Готово.

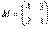– матрица миноров соответствующих элементов матрицы .

3) Находим матрицу алгебраических дополнений

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:

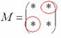
Именно у этих чисел, которые я обвел в кружок!

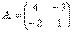– матрица алгебраических дополнений соответствующих элементов матрицы .

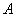И всего-то лишь…

4) Находим транспонированную матрицу алгебраических дополнений.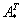

Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.

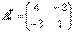– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

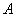Ответ.

Вспоминаем нашу формулу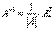
Всё найдено!

Таким образом, обратная матрица:

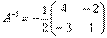
13.Определители и их свойства

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании:

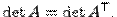
Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Непосредственная проверка доказывает данное свойство.

Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю.

Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.

Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.

Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен 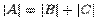, где элементыматриц B и C, за исключением элементов i-й строки (столбца), совпадают с соответствующими элементами матрицы A. A в i-х строках (столбцах) матриц B и C стоят упомянутые первые и вторые слагаемые соответственно.

Способы вычисления определителей