Задания для самостоятельной работы. В лабораторной работе студент должен выполнить в соответствии с выданным преподавателем вариантом два задания.

В лабораторной работе студент должен выполнить в соответствии с выданным преподавателем вариантом два задания.

1. Найти численное решение дифференциального уравнения в MathCAD на интервале 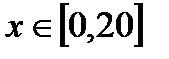. Построить график решения.

2. Численно решить систему дифференциальных уравнений в MathCAD на интервале 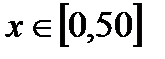. Построить графики решения.

Таблица 2

№ варианта	Задание 1	Задание 2

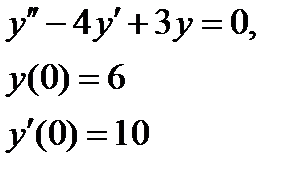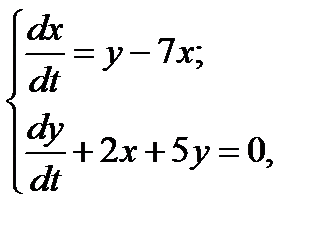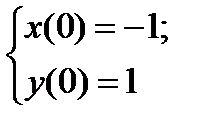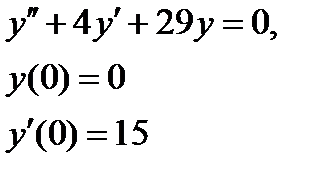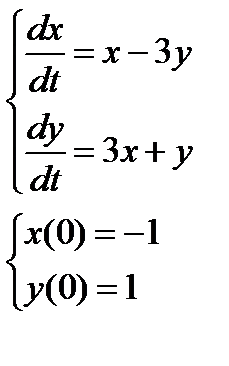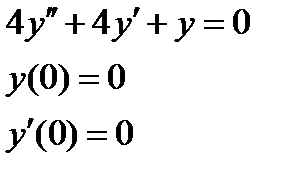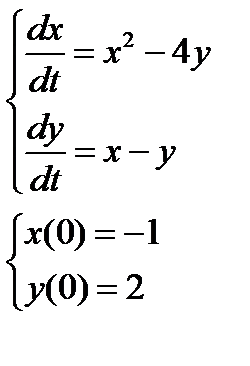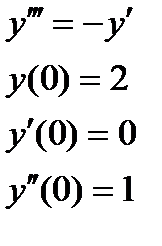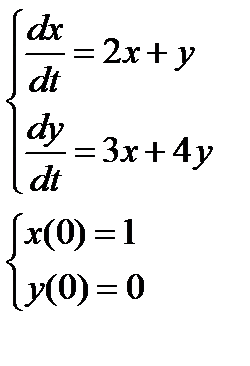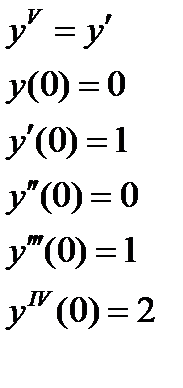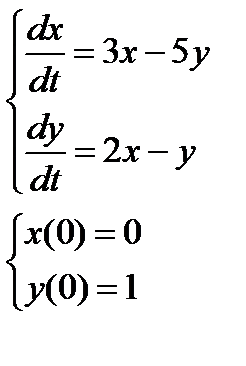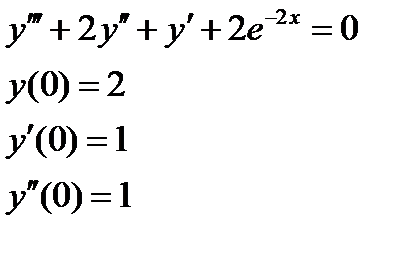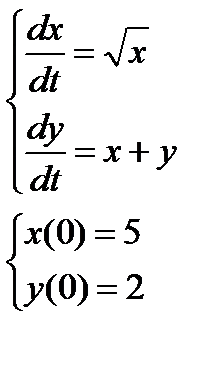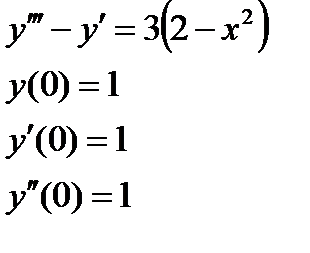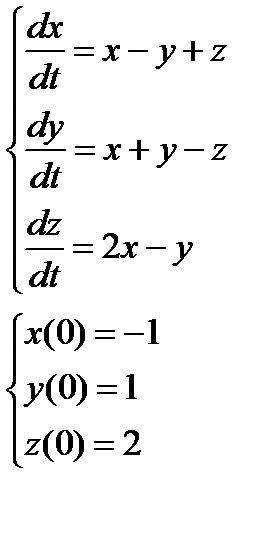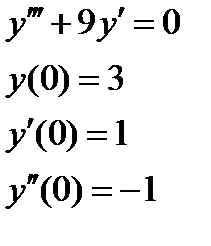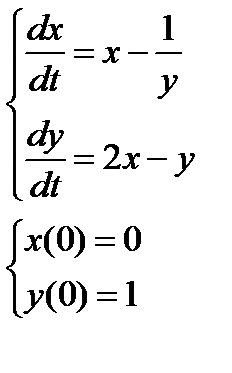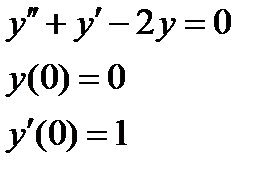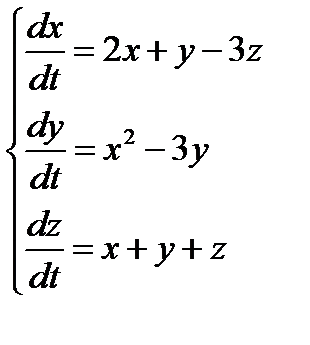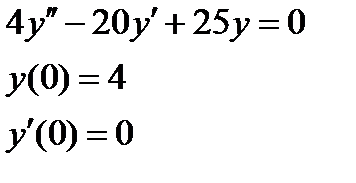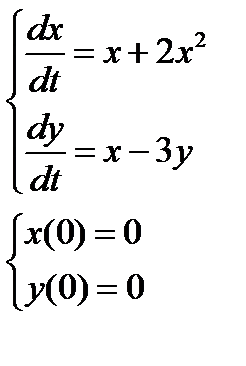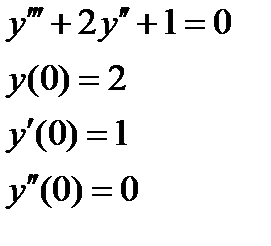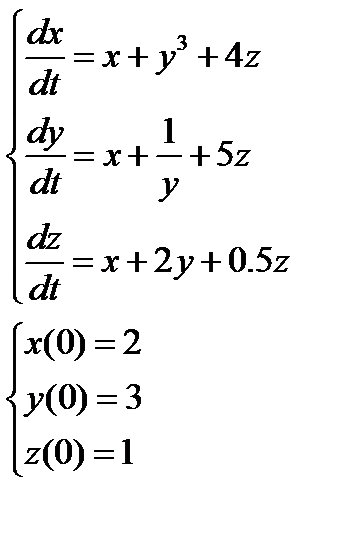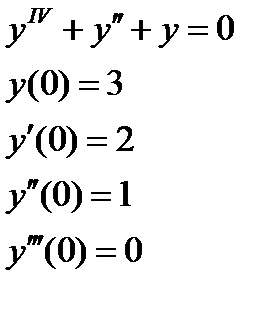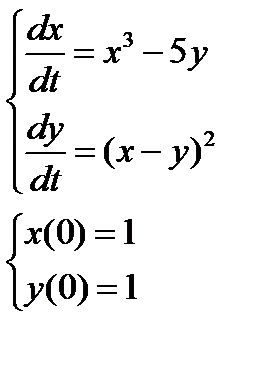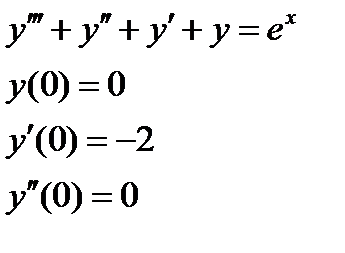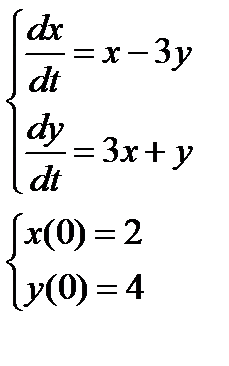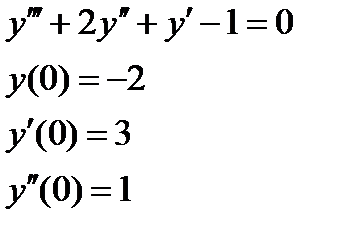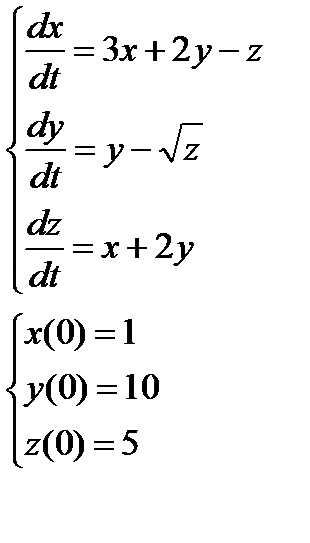Лабораторная работа №3 «Обработка данных в MathCAD»

Цель работы.

1. Изучить способы проведения интерполяции табличных данных в MathCAD.

2. Ознакомиться с функциями построения уравнений регрессии в MathCAD.

Задание.

1 Изучить методические указания по выполнению лабораторной работы.

2 Выполнить интерполяцию табличных данных и получить модель заданного вида с помощью регрессионного анализа в соответствии с вариантом задания (табл. 3).

Методические указания

Интерполяция

При проведении анализа различных физических явлений, технологических процессов результаты эксперимента обычно представляются в виде табличной зависимости функции y(x):

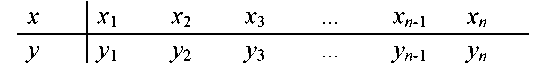
При этом число заданных точек этой зависимости ограничено.

Поэтому неизбежно возникает задача приближенного вычисления значений функции в промежутках между узловыми точками (интерполяция) и за их пределами (экстраполяция). Эта задача решается аппроксимацией или интерполяцией исходной зависимости, т.е. ее подменой какой-либо достаточно простой функцией [2]. В MathCAD имеются встроенные функции, обеспечивающие кусочно-линейную и сплайновую интерполяцию исходной табличной зависимости.

При кусочно-линейной интерполяции соседние узловые точки соединяются отрезками прямых, и дополнительные точки определяются по уравнениям этих прямых. Для проведения такого вида интерполяции используется функция linterp(VX, VY, x),

где VX и VY – векторы, задающие узловые точки исходной табличной зависимости,

x – аргумент результирующей интерполяционной функции.

Например, на рис. 6 исходная табличная зависимость y(x) задается векторами VX и VY (по 5 точек). Затем определяется, так называемая, интерполяционная функция f_i(x), которая позволяет для любого значения аргумента x определить искомую величину функции y. График этой функции представлен на рис. 6 (пунктир) вместе с узловыми точками (крестики). Из рис. 6 видно, что в узловых точках VX_i значения функции f_i(x) совпадают с табличными VY.

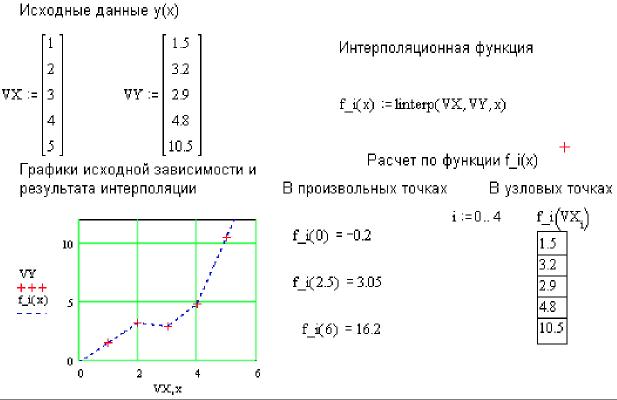
Рис. 6 Проведение кусочно-линейной интерполяции в MathCAD

Как видно из рис. 6, результаты кусочно-линейной интерполяции при достаточно малом числе узловых точек получаются довольно грубыми. Поэтому в целях повышения точности целесообразнее использовать сплайновую интерполяцию, при которой исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так, чтобы непрерывными были их первые и вторые производные.

Для выполнения сплайновой интерполяции в MathCAD имеются четыре встроенные функции. Три из них обеспечивают получение вектора вторых производных сплайн-функций при различных способах сплайновой интерполяции:

• cspline (VX, VY) – возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;

• pspline (VX, VY) – возвращает вектор VS вторых производных при приближении в опорных точках к параболической кривой;

• lspline (VX, VY) – возвращает вектор VS вторых производных при приближении в опорных точках к прямой.

Четвертая функция interp (VS, VX, VY, x) определяет для найденного ранее вектора вторых производных VS и заданной при помощи векторов VX и VY исходной табличной зависимости y(x) интерполяционную сплайновую функцию.

Таким образом, сплайновая интерполяция в MathCAD производится в два этапа. На первом этапе определяется вектор вторых производных VS при помощи одной из трех функций (cspline, pspline или lspline), а на втором – определяется интерполяционная зависимость посредством функции interp. Пример дан на рис. 7.

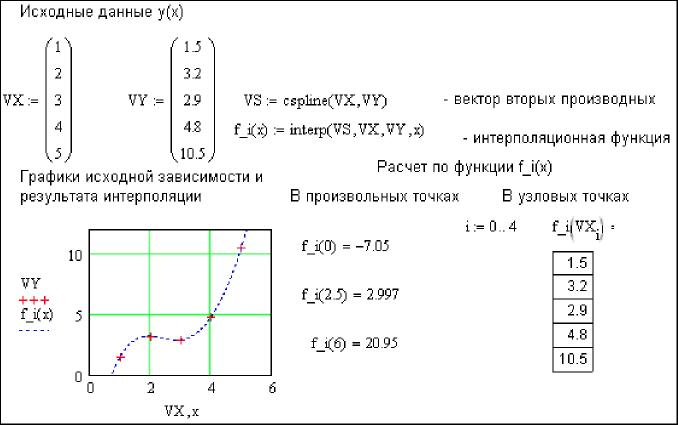
Рис. 7 Проведение сплайновой интерполяции в MathCAD

Как видно из сравнения графиков, представленных на рис. 6 и 7, сплайновая интерполяция дает более гладкий и точный график интерполяционной функции.

Регрессионный анализ

Широко распространенной задачей обработки данных является представление результатов эксперимента некоторой функцией y(x). Задача регрессионного анализа заключается в получении параметров этой функции, описывающей (аппроксимирующей) экспериментальные данные, заданные векторами VX и VY, с наименьшей среднеквадратической погрешностью (метод наименьших квадратов).

Довольно часто используется линейная регрессия, при которой аппроксимирующая функция y(x) имеет вид y(x)= a+bx , для определения коэффициентов которой в MathCAD служат следующие встроенные функции:

• intercept(VX, VY) – возвращает значение параметра a (величины отрезка, отсекаемого линией регрессии на оси OY);

• slope (VX, VY) – возвращает значение параметра b (тангенса угла наклона линии регрессии).

Пример дан на рис. 8.

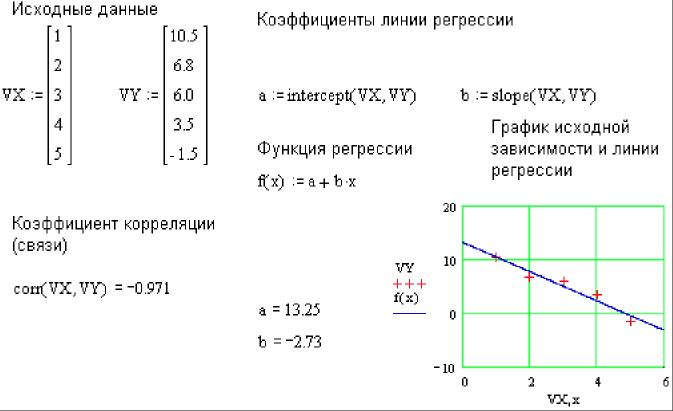
Рис. 8 Линейная регрессия

В приведенном примере (рис. 8) рассчитан коэффициент корреляции (связи) двух множеств VX и VY с помощью функции corr. Чем ближе этот коэффициент к единице по модулю, тем точнее исходные табличные данные, определенные векторами VX и VY, описываются линейной зависимостью y(x)= a+bx.

Проведение полиномиальной регрессии, т.е. аппроксимации табличной зависимости полиномом n-й степени, выполняется посредством встроенной функции regress(VX, VY, n). Данная функция возвращает вектор, назовем его k, элементы которого, начиная с четвертого, представляют собой коэффициенты аппроксимирующего полинома P_n(x)=a₀+a₁x+a₂x²+…+a_n-1x^n-1+a_nxⁿ т.е.

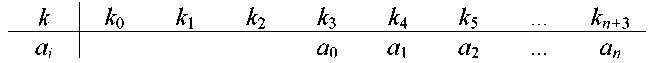
Пример выполнения полиномиальной регрессии представлен на рис. 9.

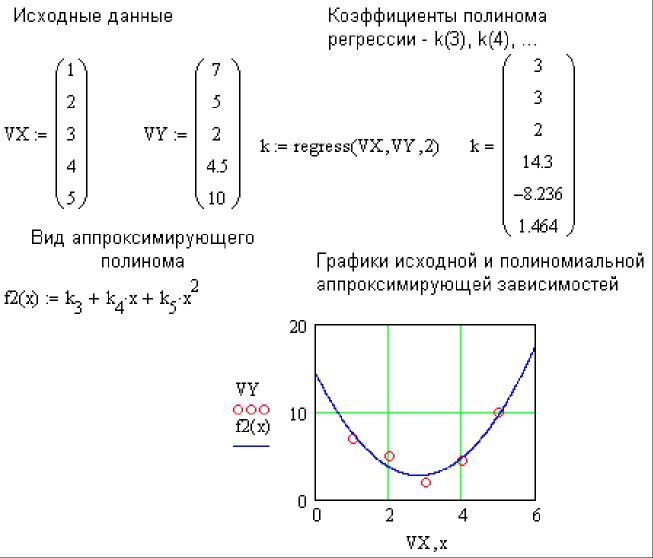
Рис. 9 Полиномиальная регрессия

Замечание. Для нахождения корней полинома произвольной степени в MathCAD используется функция polyroots.

Кроме того, в MathCAD имеется ряд других функций для проведения регрессионного анализа [2], например, linfit, loess, genfit.