Определение зависимости периода собственных колебаний пружинного маятника от массы груза и определение коэффициента упругости пружины динамическим методом

Лабораторная работа № 4

Изучение колебаний пружинного маятника

Цель работы:Изучить закономерности колебаний пружинного маятника и определить зависимость его периода собственных колебаний от массы груза.

Теоретическое введение

Простейшая колебательная система состоит из груза массой m, подвешенного на пружине, массой которой можно пренебречь по сравнению с массой груза. Такая система называемая пружинным маятником, совершает гармони-ческие колебания в соответствии с уравнением:

x = A₀cos(ω₀t +α₀), (1)

где x =∆l - удлинение пружины под действием груза, A₀ ‒ амплитуда или максимальное смещение груза от положения равновесия, α₀‒ начальная фаза колебания, ω₀ ‒ циклическая частота. Эта частота может быть выражена через период Т собственных колебаний груза известной формулой:

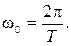(2)

Как показывает вывод, период Т колебаний груза определяется по формуле:

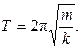(3)

Отсюда видно, что период колебания Т груза, подвешенного на пружине, не зависит от амплитуды колебаний, но зависит от массы груза m и коэффициента упругости (или жесткости) пружины k.

Экспериментальная часть

Установка представляет собой П-образный штатив, в середине которого укреплена вертикальная линейка с миллиметровой шкалой. Рядом с линейкой могут укрепляться пружины с различной жёсткостью. К концам пружин подвешиваются грузы.

Задание 1

Определение коэффициента упругости пружины статическим методом

1. Закрепите на штативе пружину и подвешивайте к ней различные грузы, изменяя их массу (5 – 6 раз). Сила тяжести грузов в соответствии с выражением (2) и будет деформи-рующей силой.

Таблица 1

mi , г	mi g , H	n	∆li , см	mi , г	mi g , H	n	∆li , см
Ср.		Ср.
Ср.		Ср.
Ср.		Ср.

2. Когда пружина после каждого подвешивания возвратится в неподвижное состояние, измерьте величину растяжения пружины, т.е. её статическую деформацию x =∆l_i. Опыт повторите не менее 3 раз для каждого из подвешиваемых грузов. Результаты измерений запишите в таблицу 1.

3. Постройте график, откладывая по горизонтальной оси величину ∆l_i, а по вертикальной оси величину приложенной силы, т.е. силу тяжести груза m_i g. Если растяжение пружины не очень велико, то выполняется закон Гука, и график будет прямой линией, проходящей через начало координат.

4. Вычислите коэффициент упругости пружины, который будет численно равен тангенсу угла наклона графика к горизонтальной оси.

Задание 2

Определение зависимости периода собственных колебаний пружинного маятника от массы груза и определение коэффициента упругости пружины динамическим методом

1. Подвесьте к одной из пружин груз и выведите маятник из положения равновесия примерно на 1 – 2 см.

2. Предоставив грузу свободно колебаться, измерьте секундомером промежуток времени, в течение которого маятник совершит 10 полных колебаний. Найдите период колебания маятника, разделив измеренный промежуток времени на число колебаний (на 10). Проведите измерения не менее 3 раз и вычислите среднее значение периода колебаний.

3. Повторите измерения с другими грузами. Результаты измерений запишите в таблицу 2.

4. Постройте зависимость средних (для каждой массы груза) значений периода колебаний маятника от величины массы груза. График будет простым, если по горизонтальной оси откладывать значения массы грузов, а по вертикальной – значения квадратов периодов.

5. По результатам измерений для каждой массы груза определите коэффициент упругости пружины динамическим методом, применяя формулу (6). Запишите значения k также в таблицу 2.

6. Аналогичные расчеты проведите для всех грузов и подсчитайте среднее значение коэффициента упругости пружины.

Таблица 2

№ измер. массы	mi , г	n	t , с	T, c	T2, c2	k , H/м
Ср.
Ср.
Ср.
Ср.
Ср.

7. Сравните полученные результаты с результатами задания 1.