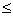Дополнение множества А называется множество ВСЕХ элементов коорые не входят в множество А

9) Запишите формулу для нахождения числа элементов объединения двух (трёх) множеств

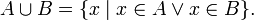
10) Какое событие называют случайным?

Любое подмножество пространства элементарных исходов 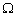будем называть случайным событием. Заметим, что при математически строгом подходе это определение должно быть уточнено, если 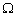не является конечным или счётным множеством. Однако такое уточнение необходимо лишь для построения теории вероятностей как раздела современной математики, оперирующей логически безупречными, но зачастую сложными для неподготовленного читателя понятиями. К тому же подмножества пространства 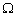, не являющиеся, строго говоря, событиями, представляют собой чистую математическую абстракцию и не встречаются в практических задачах. Поэтому в дальнейшем любое подмножество из 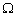мы будем рассматривать как случайное событие или просто событие.

Считается, что событие 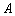произошло (наступило, реализовалось),если результатом случайного опыта явился какой-либо из элементарных исходов, входящих в подмножество .

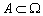Пример 1.2.1.

В примере 1.2.1 показано, что при бросании одной игральной кости 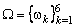. Рассмотрим события: 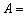{выпало 3 очка}, 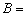{число очков кратно трём}, 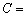{число очков нечётно}, 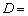{число очков не меньше двух}.

◄Очевидно, , , .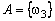

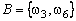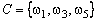11) Что называют испытанием?

???

12) Какое событие называют достоверным? Приведите примеры

Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом.

13) Какое событие называют невозможным? Приведите примеры

Невозможным, если в данном испытании оно является заведомо не может произойти.

14) Какое событие называют совместным? Приведите примеры

Два события называют совместимыми, если появление одного из них не исключает появления другого в одном и том же испытании.

Испытание - однократное бросание игральной кости. Событие А - появление четырех очков. Событие В - появление четного числа очков. События А и В совместимые.

15) Какое событие называют несовместным? Приведите примеры

Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Испытание - однократное бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.

16) Какие события называют равновозможными? Приведите примеры

Равновозможными считают события, если нет оснований полагать, что одно событие является более возможным, чем другие.

17) Какие события называют противоположными? Приведите примеры

Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через .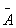

Испытание - бросание монеты. Событие А - выпадение герба, событие В - выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого.

18) Что называют полной группой событий? Приведите примеры событий, образующих полную группу.

Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.

Примеры полных групп событий: выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости.

19) Какие исходы испытания называют элементарными?

Рассмотрим полную группу попарно несовместимых событий U₁, U₂, ., U_n, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий 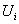, (i = 1,2, ..., n) равновозможное, т.е. условия испытания не создают преимущества в появлении какого-либо события перед другими возможными. События U₁, U₂,..., U_n, образующие полную группу попарно несовместимых и равновозможных событий, называется элементарными событиями.

20) Какие элементарные исходы называют благоприятствующими данному событию?

Событие А называют благоприятствующим событию В, если наступление события А влечет за собой наступление события В.

Пусть при бросании игральной кости события U₂, U₄, и U₆ -появление соответственно двух, четырех и шести очков и А - событие, состоящее в появлении четного числа очков; события U₂, U₄ и U₆ благоприятствуют событию А.

21) Сформулируйте классическое определение вероятности?

Вероятностью Р(А) события А называют отношение 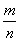числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т.е.

Р(А)= .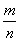

Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А - выпадение герба и событие В — выпадение цифры образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно событие - само А, т.е. здесь m = 1. Поэтому

Р(А) = .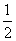

Найти вероятность того, что при бросании игральной кости выпадет число очков, делящееся на 2 (событие А).

Число элементарных событий здесь 6. Число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому Р(А)= = .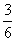

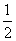Из приведенного классического определения вероятности вы­текают следующие ее свойства [1, 510].

Свойства классического определения вероятности

1. Вероятность достоверного события равна единице. Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n и, следовательно,

Р(А)= 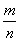= =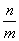1.

2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда

Р(А)= 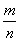= =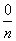0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n и, значит, 0 < 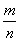< 1. Следовательно, 0 < Р(А) < 1.

Итак, вероятность любого события удовлетворяет двойному неравенству, 0 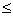Р(А)