Управление конечным состоянием

В ряде задач характер движения объекта в процессе управления интереса не представляет, а существенным является только состоя­ние х_п, в которое переходит объект по окончании про­цесса управления. При этом критерием качества управ­ления будет служить значение целевой функции в конце процесса управления, т е. величина

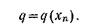
Рассмотрим путь поиска оптимального управления 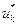. На метода Беллмана конечным состоянием, который заключается в том, что если система находилась в состоянии 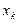, то необходимо найти оптимальное управление 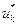, которое на последующих шагах k+1,…,n приводило бы к максимуму целевую функцию .

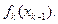Функция 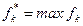носит название локального оптимума на k-м шаге (условный оптимум).

Беллман предложил следующий путь поиска локального оптимума. Записывается уравнение целевой функции на k-м шаге в виде:

,

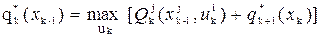где 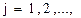m- число возможных подсостояний х_к , 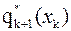- оптимальная (максимальная) целевая функция или локальный оптимум на k+1 шаге; i=1,…z - число возможных подуправлений U_k.

Из уравнения видно, что оптимальная целевая функция на k-м шаге определяется путем поиска максимума суммы оптимальной целевой функции на (k+1)-м шаге и эффективности перехода из (k-1)-го состояния в

k-е состояние.

Пользуясь указанной формулой, Беллман предложил локальную оптимальную целевую функцию, а следовательно, и оптимальное управление для каждого k-го состояния определять, начиная с конечного состояния 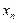, т.е. двигаясь с конца к исходному состоянию. Такое предложение позволяет существенно упростить расчеты, т.к.

,

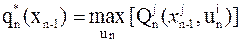а для вычисления целевой функции на (n-1)-м шаге используется уже известная оптимальная целевая функция на n-м шаге :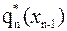

.

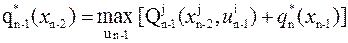Зная оптимальную целевую функцию на (n-1)-м шаге, можно найти оптимальную целевую функцию на (n-2)-м шаге и т.д. до 1-го шага.

Таким образом, можно построить ряд локальных (условных) оптимумов. Условность состоит в том, что оптимальный переход осуществляется из состояния . Ряд условных оптимумов представляется в виде последовательности

.

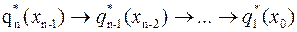Для каждого условного оптимума определяется условное оптимальное управление в виде последовательности

.

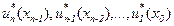Окончательным решением задачи является определение безусловных оптимумов и безусловных оптимальных управлений, т.е. необходимо выстроить обратный ряд ряд вида:

.

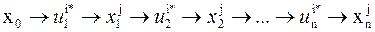Методика построения и решения задачи средствами

динамического программирования

Построение задачи ведется в следующей последовательности.

1. В поставленной задаче выделяются состояния 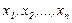и выбирается способ деления процесса на шаги k=1,…, n.

2. Каждое из состояний x_k представляется в виде множества подсостояний 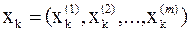и определяется управление .

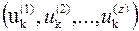3. Записывается уравнение, определяющее состояние 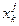, являющееся функцией предыдущего состояния 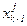и управления 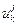, в виде 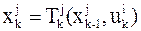; j =1,…m, i=1,…, z..

4. Вводится показатель эффективности для каждого k-го перехода .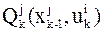

5. Составляется общая целевая функция в виде суммы эффективностей на k-х шагах .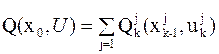

6. Для наглядности можно построить граф модели.

Этапы решения задачи следующие.

1. Записываются уравнения Беллмана для k-го и n-го шагов в виде:

,

.

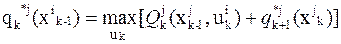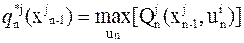2. Определяется ряд условных оптимальных управлений .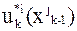

3. Строится ряд безусловных оптимумов и безусловного оптимального управления. Если начальное состояние x₀ единственное, то максимум

общей целевой функции равен условному оптимуму 1-го перехода .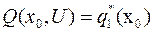

Далее выстраивается ряд .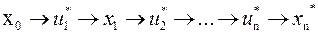

Выполняется это следующим образом. Предполагается, что система находится в состоянии x₀ . Из всех вариантов перехода на первом шаге выбирается тот, у которого 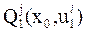максимален. Исходя из этого выбирается оптимальное 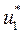. Указанная процедура повторяется для всех последующих состояний .

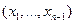4. Если начальных состояний x₀ⁱ несколько i=1,…m и они составляют множество 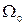, то максимум целевой функции определяется по формуле .

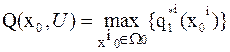Далее строится ряд 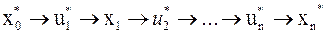.