Расчет цепей постоянного тока методом контурных токов и методом эквивалентного генератора
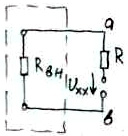 М-д эквивалентного генератора. Позволяет опр-ть ток в отдельно взятой ветви не опред-я ток в отд-х ветвях.
М-д эквивалентного генератора. Позволяет опр-ть ток в отдельно взятой ветви не опред-я ток в отд-х ветвях.
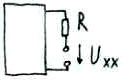
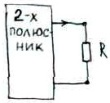
а) разрывается ветвь, в которой необходимо определить ток.
б)опр–ся любым изв. методом напряж. холостого хода т.е. напряж м/у т. разрыва ветвей.
в) опр-ся сопротивление Rвн остальной цепи по отношению к зажимам а и в, при этом счит., что ИЭ в этой части цепи отсутствуют и замены их - внутренними сопротивлениями.
г)Опр-ем искомый ток ветви по фор-ле I=Uxx/(Rвн+R)
Метод контурных токов. Метод предполагает, что в каждом независимом контуре протекает так называемый контурный ток, кот. замыкается только по своему контуру, оставаясь вдоль него неизменяемым. Число незав-х контуров опр-ся ур-ем: y=p–n+1; p-число ветвей, n-число узлов.
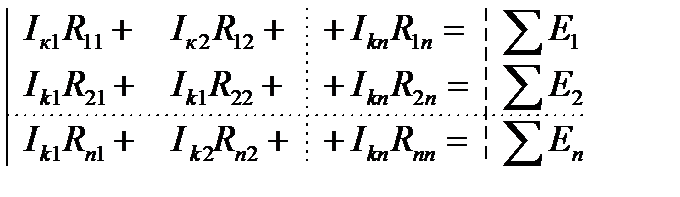
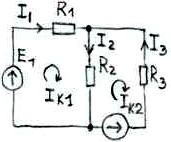 Если в схеме сущ. y–независ контуров, значит в ней протекает y–контурных токов, то составл-я y–ур-ий с y–неизв. Сопротивл вида R11,R22,Rnn-это собств-е сопрот. контура n равное сумме всех сопротивлений, входящих в этот контур. Сопр-е вида Rkf – сопр-е ветви общей для конт-ов k и f, причем это сопротивление берется с "+", если направление контур-х токов в ветви общей для контуров совпадает, если не совпадают "–". Правая часть ур-й SEn предст-т собой алгебраич. сумму всех ЭДС входящих в контур. ЭДС, направление кот. совпад. с направлением контур-го тока берутся со знаком "+ " и наоборот.
Если в схеме сущ. y–независ контуров, значит в ней протекает y–контурных токов, то составл-я y–ур-ий с y–неизв. Сопротивл вида R11,R22,Rnn-это собств-е сопрот. контура n равное сумме всех сопротивлений, входящих в этот контур. Сопр-е вида Rkf – сопр-е ветви общей для конт-ов k и f, причем это сопротивление берется с "+", если направление контур-х токов в ветви общей для контуров совпадает, если не совпадают "–". Правая часть ур-й SEn предст-т собой алгебраич. сумму всех ЭДС входящих в контур. ЭДС, направление кот. совпад. с направлением контур-го тока берутся со знаком "+ " и наоборот.
Действительный ток протек-й в ветви принадлеж-й только одному контуру численно = контур-у току, а ток в ветви принадлеж. нескольким контурам = алгебраич. сумме контурных токов, проходящей ч/з ветвь.
Цепи однофазного переменного тока
1. Получение синусоидальной ЭДС. Основные величины, характеризующие хар-ие синусоед. Ф-ии времени.
Линейные цепи однофазного синусоидального тока.Эл. цепи в кот. значение и направл. ЭДС, напряж., тока переодически изменяются во времени по синусид-му закону наз-ся цепями пременного синусоид-го тока. Мгновенное значение перем-го тока в любой заданный момент времени, наз-ся мгн. знач. тока.
Способы получения синусоид-ых ЭДС:можно исп-ть проводник в виде прямоуг рамки, к-я вращ с пост угл скор ω в пост маг поле.V-лин. скор. движ. рамки. VН-скор. пересе. маг. силовых линий. wt - угол поворота витка за время t, относ. начала отсчета.
Соглас з-ну эл-маг индукции при вращ рамки в кажд продольном проводнике наводится ЭДС e=BlVН, B-маг индукц. VН=V*sin(wt+φ) => e=Bl*V*sin(wt+φ)=Em*sin(wt+φ), где Em – амплитуда. l-длина проводника.
Осн велич:в лин цепях синус тока напряж, эдс и ток явл синус ф-ями времени: u= Umsin(wt+j), i= Imsin(wt+j), e= Emsin(wt+j), u,I,e – мгнов знач, (wt+j)-аргумент син.ф-ии(фаза или фазовый угол).
Кажд син ф-я времени хар-ся 3-мя параметрами.1.АмплитудаUm,Im,Em -макс знач.ф-ии. 2.Угл частота w.скорость изм. аргумента син.ф-ии(рад/с). 3.Нач фаза ju, je, ji.-изм. аргумента син.ф-ии в мом врем t=0(рад).
Для хар-ки синусоид ф-ии вр исп след парам: 1.период Т=2π/ω - миним интервал времени, по истеч к-го мгнов знач повтор .2.частота f=1/T - число периодов в сек (Гц). 3. Сдвиг фаз м/д током и напряж φ=φu-φi. 4.действующ знач U, E, I – среднеквадратич знач перемен величины за период, т.е I=I_m⁄√2 (для u,e).
Средн.значение син. ф-ии. за период = 0, поэтому условились считать под ср. знач. её ср. знач. за положит. полупериод.
2.Амплитудные, действующие и ср.знач. син. ф-ии(см вопр выше)
