Задачи, связанные с применением второго замечательного предела
Предел последовательности
Определение. Число а называется пределом последовательности 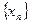 , если для любого
, если для любого  существует номер N такой, что при всех n>N выполняется неравенство
существует номер N такой, что при всех n>N выполняется неравенство 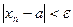
( 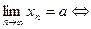
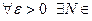
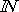
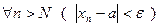 ).
).
Пример 1. Доказать, что  (указать
(указать 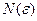 ).
).
Решение. Неравенство 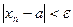 из определения предела последовательности, которое мы должны решить относительно n, принимает вид
из определения предела последовательности, которое мы должны решить относительно n, принимает вид 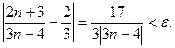 Пусть
Пусть 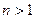 . Тогда
. Тогда 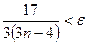 , откуда
, откуда 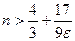 , следовательно, в качестве N можно взять
, следовательно, в качестве N можно взять 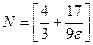 . Здесь
. Здесь  - целая часть числа
- целая часть числа 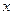 , то есть наибольшее целое число, не превосходящее
, то есть наибольшее целое число, не превосходящее 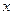 . Если, например,
. Если, например, 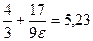 , то условиям задачи отвечают натуральные числа
, то условиям задачи отвечают натуральные числа 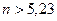 , то есть
, то есть 
Пример 2. Доказать, что 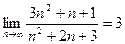 (указать
(указать 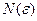 ).
).
Решение. Неравенство 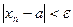 принимает вид
принимает вид 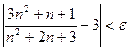 ,
, 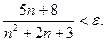 Последнее неравенство преобразуется в квадратное. Однако вычисления можно упростить. Неравенство будет выполняться, если справедливо следующее двойное неравенство:
Последнее неравенство преобразуется в квадратное. Однако вычисления можно упростить. Неравенство будет выполняться, если справедливо следующее двойное неравенство: 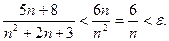 Его левая часть заведомо выполняется при
Его левая часть заведомо выполняется при 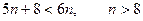 . Правая часть выполняется при
. Правая часть выполняется при 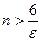 . Следовательно, условиям задачи отвечают числа
. Следовательно, условиям задачи отвечают числа 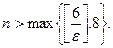 Отсюда
Отсюда 
При вычислении предела  в случае
в случае 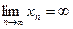 и
и 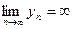 (т.е. в случае неопределённости вида
(т.е. в случае неопределённости вида 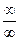 ) или в случае
) или в случае 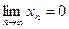 ,
, 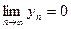
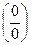 и т.д. нельзя сразу воспользоваться арифметическими свойствами предела. Следует так преобразовать выражение
и т.д. нельзя сразу воспользоваться арифметическими свойствами предела. Следует так преобразовать выражение 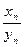 , чтобы можно было использовать свойства предела и раскрыть неопределённость, т.е. найти предел. Полезным для этого в случае
, чтобы можно было использовать свойства предела и раскрыть неопределённость, т.е. найти предел. Полезным для этого в случае 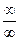 бывает вынести в числителе и знаменателе старшие степени за скобки или разделить числитель и знаменатель на старшую степень одного из них.
бывает вынести в числителе и знаменателе старшие степени за скобки или разделить числитель и знаменатель на старшую степень одного из них.
Пример 3.Найти предел  .
.
Решение. Преобразуем исходное выражение, выполнив действия в числителе и знаменателе:
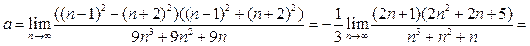
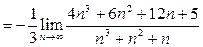 . Разделив числитель и знаменатель на их старшую степень
. Разделив числитель и знаменатель на их старшую степень 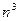 , получим
, получим 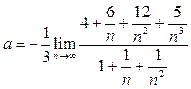 . Поскольку
. Поскольку 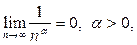 то по свойствам предела получаем
то по свойствам предела получаем 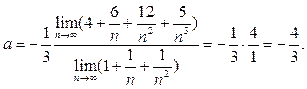
Вообще предел отношения двух многочленов переменной 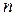 можно находить по правилу
можно находить по правилу
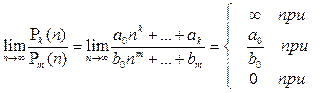
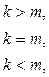 (1)
(1)
так что в решении последнего примера можно было обойтись без деления на 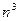 .
.
При вычислении пределов используют формулу бинома Ньютона
 (2)
(2)
Также следует знать формулу  ( «эн-факториал»- произведение натуральных чисел от 1 до n; например,
( «эн-факториал»- произведение натуральных чисел от 1 до n; например, 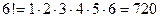 ).
).
Пример 4. Найти предел 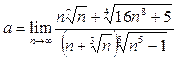 .
.
Решение. Разделим числитель и знаменатель исходного выражения на  -
-
старшую степень числителя и знаменателя. Действительно, показатель степени суммы равен наибольшему показателю степени слагаемых, поэтому для числителя он равен 2 ( 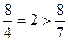 ). Показатель степени произведения равен сумме показателей степеней сомножителей. Показатели степени выражений
). Показатель степени произведения равен сумме показателей степеней сомножителей. Показатели степени выражений 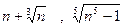 равны 1, поэтому показатель степени знаменателя равен 1+1=2. Тогда
равны 1, поэтому показатель степени знаменателя равен 1+1=2. Тогда 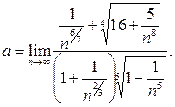 Поскольку
Поскольку 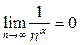 при
при 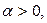 то
то 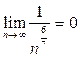 ,
, 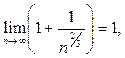
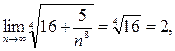
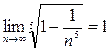 и по свойствам предела получаем
и по свойствам предела получаем 
При вычислении пределов, содержащих иррациональные выражения, часто используют приём перевода иррациональности из числителя в знаменатель или наоборот с помощью формул сокращённого умножения
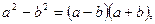 (3)
(3)
 (4)
(4)
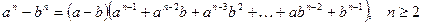 (5)
(5)
(первая и вторая из них получаются из третьей при  и
и 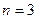 соответственно).
соответственно).
Так, например, если выражение содержит множитель  , где
, где 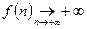 и
и  и их старшие степени и коэффициенты при них совпадают или эта разность стремится к нулю, полезно умножить числитель и знаменатель исходной дроби на
и их старшие степени и коэффициенты при них совпадают или эта разность стремится к нулю, полезно умножить числитель и знаменатель исходной дроби на 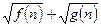 , т.е. на выражение, сопряжённое к
, т.е. на выражение, сопряжённое к  .
.
Пример 5. Найти предел 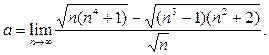
Решение. Имеем неопределённость 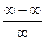 .Умножим числитель и знаменатель дроби на выражение, сопряжённое к числителю и воспользуемся формулой (3); далее разделим числитель и знаменатель на
.Умножим числитель и знаменатель дроби на выражение, сопряжённое к числителю и воспользуемся формулой (3); далее разделим числитель и знаменатель на 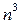 :
:

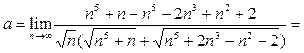
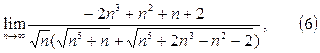
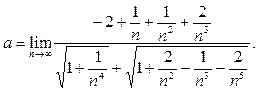 Теперь воспользуемся арифметическими свойствами предела и тем, что
Теперь воспользуемся арифметическими свойствами предела и тем, что 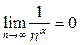 при
при 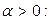
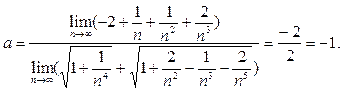
Замечание. Сразу после (6) можно было записать 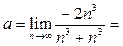
 , поскольку показатели степени слагаемых в знаменателе
, поскольку показатели степени слагаемых в знаменателе 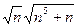 и
и 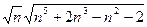 равны 3, следовательно, старшая степень знаменателя есть
равны 3, следовательно, старшая степень знаменателя есть 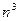 и коэффициент при
и коэффициент при 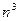 равен 2 (на языке асимптотического поведения функций выражение в знаменателе эквивалентно
равен 2 (на языке асимптотического поведения функций выражение в знаменателе эквивалентно 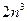 , то есть
, то есть
 ,
, 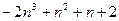 эквивалентно
эквивалентно 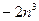 , а при вычислении пределов величины можно заменять на эквивалентные, см. с.11).
, а при вычислении пределов величины можно заменять на эквивалентные, см. с.11).
Пример 6. Найти предел 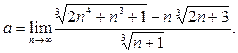
Решение. Имеем неопределённость 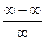 . Воспользуемся формулой (4).Умножим числитель и знаменатель дроби на выражение, дополняющее числитель до разности кубов, то есть на соответствующий неполный квадрат суммы; далее разделим числитель и знаменатель на
. Воспользуемся формулой (4).Умножим числитель и знаменатель дроби на выражение, дополняющее числитель до разности кубов, то есть на соответствующий неполный квадрат суммы; далее разделим числитель и знаменатель на 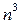 и воспользуемся арифметическими свойствами предела:
и воспользуемся арифметическими свойствами предела:

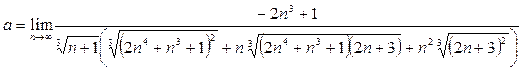 . (7)
. (7)
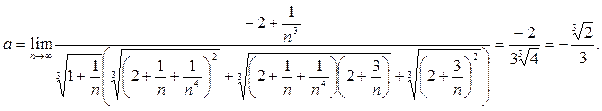
Замечание. Сразу после (7) можно было записать 
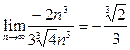 (см. предыдущее замечание).
(см. предыдущее замечание).
Пример 7. Найти предел 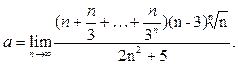
Решение.Поскольку  , то
, то 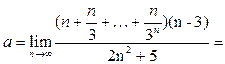
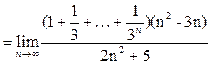 . Первый сомножитель в числителе является суммой геометрической прогрессии. Найдём эту сумму по формуле
. Первый сомножитель в числителе является суммой геометрической прогрессии. Найдём эту сумму по формуле 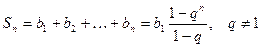 :
: 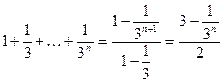 . Так как
. Так как 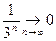 , то
, то 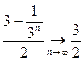 . Окончательно получаем
. Окончательно получаем 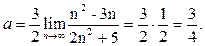
Пример 8. Найти предел 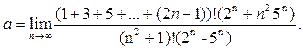
Решение. Воспользуемся формулой суммы арифметической прогрессии 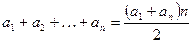 :
: 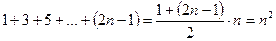 . Кроме того,
. Кроме того, 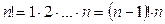 , откуда
, откуда 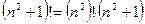 . Подставляем полученные выражения в исходное:
. Подставляем полученные выражения в исходное:

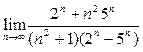 .
.
Разделим теперь числитель и знаменатель последовательно на  и
и 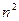 :
:
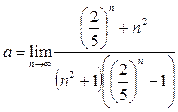
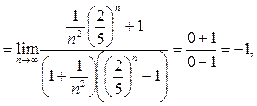 поскольку
поскольку 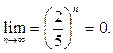
Пример 9. Найти предел 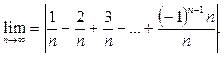
Решение. Обозначим  Если
Если 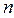 - чётное,
- чётное,  , то
, то  Если
Если 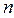 - нечётное,
- нечётное, 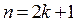 , то
, то
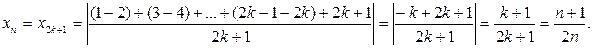
Таким образом, при любом 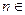
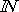
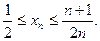 Поскольку
Поскольку 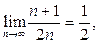 то
то 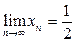 .
.
Задачи, связанные с применением теоремы Вейерштрасса о пределе монотонной последовательности.
Пример 10. Доказать, что 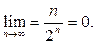
Решение. 1-й способ. Обозначим  Заметим, что
Заметим, что  при
при 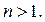 Поэтому последовательность
Поэтому последовательность 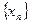 убывает при
убывает при 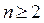 и, поскольку она ограничена снизу нулём, то имеет предел. Обозначим
и, поскольку она ограничена снизу нулём, то имеет предел. Обозначим  и перейдём к пределу в равенстве
и перейдём к пределу в равенстве 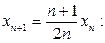
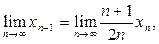
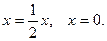
2-й способ. Используя формулу (2), получаем 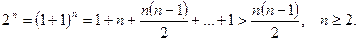 Отсюда
Отсюда 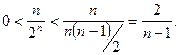 Поскольку
Поскольку 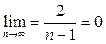 , из последнего неравенства следует, что
, из последнего неравенства следует, что 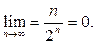
3-й способ. Найдём 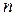 , при которых выполняется неравенство
, при которых выполняется неравенство 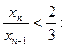
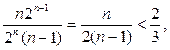
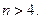 Следовательно, при
Следовательно, при 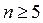
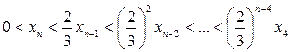 , то есть
, то есть 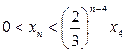 . Поскольку
. Поскольку 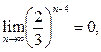 то из последнего неравенства следует, что
то из последнего неравенства следует, что 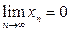 .
.
Пример 11. Доказать, что последовательность 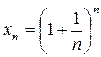 монотонно возрастает и ограничена сверху, а последовательность
монотонно возрастает и ограничена сверху, а последовательность 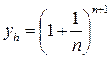 монотонно убывает и ограничена снизу. Отсюда вывести, что эти последовательности имеют общий предел
монотонно убывает и ограничена снизу. Отсюда вывести, что эти последовательности имеют общий предел 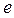 .
.
Второй замечательный предел
задаётся формулами 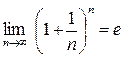 ,
, 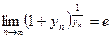 , где
, где 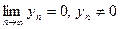
или формулой (). Он применяется, в частности, при вычислении пределов
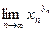
 , где
, где 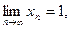
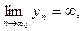 т.е. в случае неопределённости вида
т.е. в случае неопределённости вида 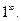
Пример 12.Найти предел 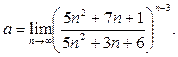
Решение.Находим пределы основания и показателя степени исходного выражения и убеждаемся в том, что перед нами неопределённость вида 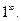 Выделяем в исходном выражении формулу
Выделяем в исходном выражении формулу 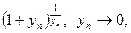 и вычисляем предел.
и вычисляем предел.
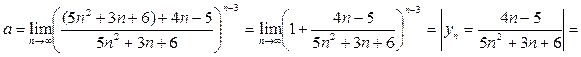

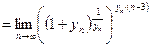
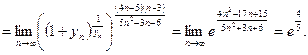
Пример 13. Пользуясь критерием Коши, доказать расходимость последовательности 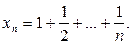
Пример 14. Доказать, что 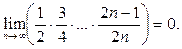
Решение. Покажем, что при любом 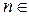
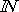
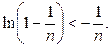
Действительно, это неравенство равносильно неравенствам
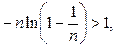



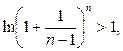
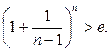
Последнее неравенство верно, поскольку последовательность 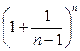
убывает(см. пример ) и её предел равен 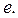 Тогда
Тогда
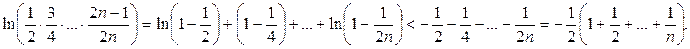
Поскольку  то
то 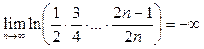 и
и
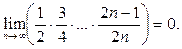
Пример 15. Для нахождения 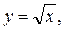
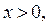 применяется следующий процесс:
применяется следующий процесс: 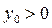 произвольно,
произвольно,
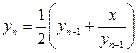
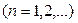 (8)
(8)
Доказать, что 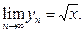
Решение. Из известного неравенства  , связывающего среднее арифметическое и среднее геометрическое двух неотрицательных чисел, получаем, что для любого
, связывающего среднее арифметическое и среднее геометрическое двух неотрицательных чисел, получаем, что для любого 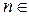
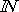
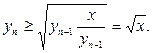 Теперь убедимся в том, что последовательность
Теперь убедимся в том, что последовательность 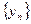 не возрастает. Действительно, неравенство
не возрастает. Действительно, неравенство 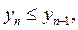 то есть
то есть  , равносильно
, равносильно 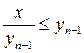 ,
, 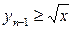 . В справедливости последнего неравенства мы убедились выше. По теореме Вейерштрасса последовательность
. В справедливости последнего неравенства мы убедились выше. По теореме Вейерштрасса последовательность 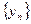 имеет предел
имеет предел 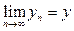 , который находим, переходя в (8) к пределу:
, который находим, переходя в (8) к пределу: 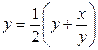 ,
, 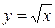 .
.
Пример 16. Последовательность 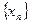 определяется следующим образом:
определяется следующим образом:
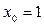 ,
, 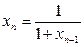
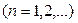 Найти
Найти 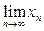 .
.
Решение. Оценим разность между 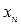 и числом
и числом  , являющимся корнем уравнения
, являющимся корнем уравнения 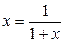 :
:  ,
,  . Применяя полученное неравенство к разности
. Применяя полученное неравенство к разности 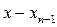 и т.д., получим
и т.д., получим 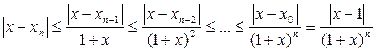 ,
, 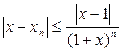 .
.
Поскольку 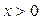 , то
, то 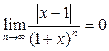 и
и  .
.
Предел функции
Пусть Е- некоторое непустое подмножество множества R действительных чисел,  – предельная точка множества Е,
– предельная точка множества Е,  - функция, определённая на Е.
- функция, определённая на Е.
Определение. Число  называется пределом функции
называется пределом функции  в точке
в точке  , если
, если
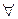 e
e 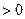
 d>0
d>0 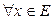
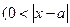
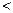 d Þ
d Þ 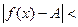 e). (9)
e). (9)
Предел функции в точке  обозначается символом
обозначается символом 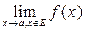 . Во всех рассматриваемых далее примерах функция определена в некоторой проколотой окрестности точки
. Во всех рассматриваемых далее примерах функция определена в некоторой проколотой окрестности точки  , поэтому мы будем использовать символ
, поэтому мы будем использовать символ 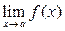 . Определение предела в случае
. Определение предела в случае 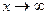 аналогично приведённому ( его можно найти в учебнике или конспекте лекций).
аналогично приведённому ( его можно найти в учебнике или конспекте лекций).
Определение. Функция  есть бесконечно малая при
есть бесконечно малая при 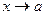 , если
, если 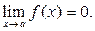
Функции  и
и 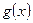 называются эквивалентными (f ~ g) при
называются эквивалентными (f ~ g) при 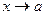 , если в некоторой проколотой окрестности точки а выполнено соотношение
, если в некоторой проколотой окрестности точки а выполнено соотношение 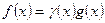 , где
, где 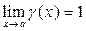 .
.
Определение. Функция  есть бесконечно малая относительно
есть бесконечно малая относительно 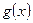 при
при 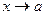 , если в некоторой проколотой окрестности точки а выполнено соотношение
, если в некоторой проколотой окрестности точки а выполнено соотношение  , где
, где  При этом пишут
При этом пишут 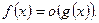 Если при этом g- бесконечно малая, то говорят, что f есть бесконечно малая более высокого порядка по сравнению с g.
Если при этом g- бесконечно малая, то говорят, что f есть бесконечно малая более высокого порядка по сравнению с g.
Справедливы следующие предложения.
1. (f(х) ~ g(х)) при 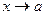
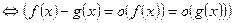 .
.
2. (f(х) ~ g(х)) при 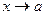
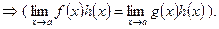
Последнее правило не распространяется на суммы и разности функций, кроме отдельных случаев, например
3. Если f(х) ~ах и g(х) ~bх и 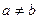 , то (f(х) - g(х)) ~(а- b)х.
, то (f(х) - g(х)) ~(а- b)х.
При вычислении пределов функций полезно использовать таблицу эквивалентных бесконечно малых величин при  :
:
1. sinx~x ,  ,
,
2. arcsinx~x, arcsinx =x+o(x),
3. tgx~x , tgx=x+o(x),
4. arctgx ~x, arctgx=x+o(x),
5. 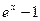 ~x ,
~x , 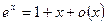 ,
,
6. 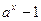 ~xlna,
~xlna, 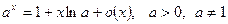 ,
,
7.  ~x ,
~x , 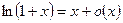 ,
,
8. 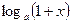 ~
~ 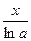 ,
, 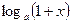
 ,
,
9. 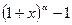 ~
~ 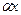 ,
, 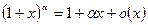 ,
,
10. 1-cosx~ 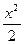 ,
, 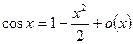 .
.
Пример 17. Доказать (найти d(e)), что  .
.
Решение. Заметив, что квадратный трёхчлен 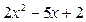 имеет корни
имеет корни 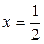 и
и 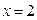 , упростим исходное выражение:
, упростим исходное выражение:
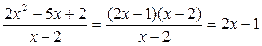 .
.
Тогда соответствующая часть формулы (9) из определения предела функции принимает вид 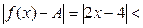 e. Это неравенство будет выполняться, если
e. Это неравенство будет выполняться, если 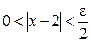 . Следовательно, можно взять
. Следовательно, можно взять  .
.
Пример 18. Найти предел 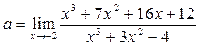 .
.
Решение. При 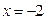 многочлены в числителе и знаменателе исходного выражения обращаются в нуль, следовательно, их пределы в точке
многочлены в числителе и знаменателе исходного выражения обращаются в нуль, следовательно, их пределы в точке 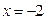 равны нулю и мы имеем неопределённость вида
равны нулю и мы имеем неопределённость вида 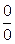 . Преобразуем исходное выражение. Разложим многочлены в его числителе и знаменателе на множители, воспользовавшись тем, что
. Преобразуем исходное выражение. Разложим многочлены в его числителе и знаменателе на множители, воспользовавшись тем, что 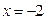 является их корнем, с помощью группировки слагаемых или разделив их на х+2:
является их корнем, с помощью группировки слагаемых или разделив их на х+2:
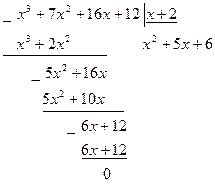
 ,
,  .
.
Получаем 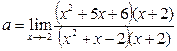
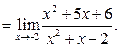 Мы снова имеем неопределённость, так как при х= -2 числитель и знаменатель последней дроби обращаются в нуль. Разлагаем их на множители, сокращаем и находим искомый предел:
Мы снова имеем неопределённость, так как при х= -2 числитель и знаменатель последней дроби обращаются в нуль. Разлагаем их на множители, сокращаем и находим искомый предел: 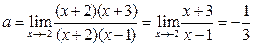 .
.
Пример 19. Найти предел
 .
.
Решение. Имеем неопределённость вида 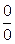 . Преобразуем исходное выражение, умножив его числитель и знаменатель на множитель
. Преобразуем исходное выражение, умножив его числитель и знаменатель на множитель 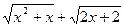 , сопряжённый к числителю.
, сопряжённый к числителю.
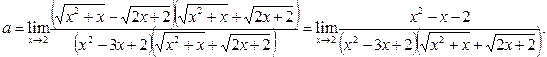
Поскольку 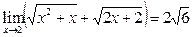 , то
, то
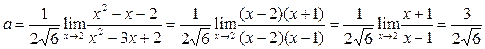 .
.
Пример 20. Найти предел 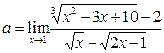 .
.
Решение. Подставив х=1 в выражения в числителе и знаменателе, убеждаемся в том, что имеется неопределённость вида 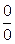 . Воспользуемся формулами (3), (4). Умножим числитель и знаменатель исходного выражения на множитель
. Воспользуемся формулами (3), (4). Умножим числитель и знаменатель исходного выражения на множитель 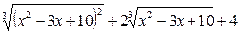 , дополняющий числитель до разности кубов (неполный квадрат суммы), и на множитель
, дополняющий числитель до разности кубов (неполный квадрат суммы), и на множитель 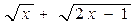 , сопряжённый к знаменателю. Получаем
, сопряжённый к знаменателю. Получаем
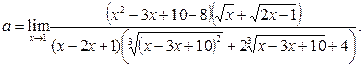 Поскольку
Поскольку 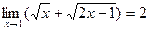 ,
, 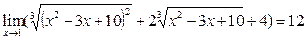 , то
, то
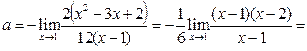
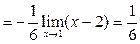 .
.
Пример 20. Найти предел 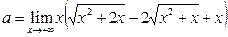 .
.
Решение. Дважды применим приём умножения на сопряжённое выражение.
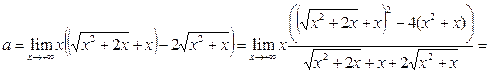
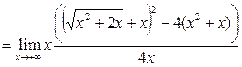 , поскольку
, поскольку 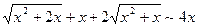 при
при 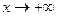 .
.
Далее, 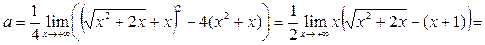
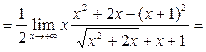
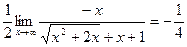 .
.
Пример 21. Найти предел a 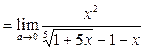 .
.
Решение. Применим формулу (5)  , положив в ней
, положив в ней 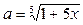 ,
, 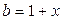 . Умножив числитель и знаменатель исходной дроби на выражение
. Умножив числитель и знаменатель исходной дроби на выражение 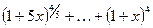 и учитывая, что оно стремится к 5, получаем:
и учитывая, что оно стремится к 5, получаем:
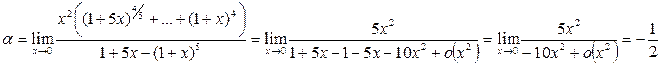
Пример 22. Найти предел 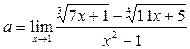 .
.
Решение. 1-й способ. Сделаем замену переменной: 

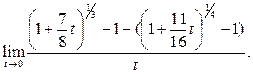 По
По
предложению 3 выражение в числителе эквивалентно 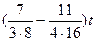 , следовательно,
, следовательно, 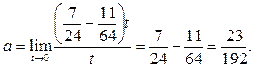
2-й способ. Сделаем замену переменной и воспользуемся формулой 9 из таблицы эквивалентных бесконечно малых.
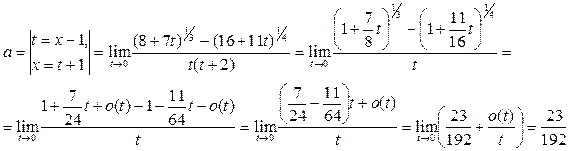
Пример 23. Вычислить предел функции
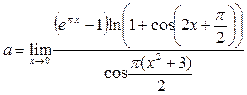 .
.
Решение. Воспользовавшись формулами приведения и табличными эквивалентностями, получаем
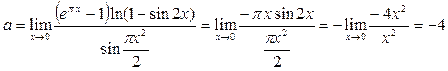 .
.
Пример24. Вычислить предел функции
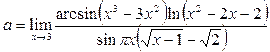 .
.
Решение. Заметив, что все сомножители в числителе и знаменателе исходного выражения есть бесконечно малые при 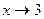 , заменим их, кроме
, заменим их, кроме  , на эквивалентные:
, на эквивалентные:
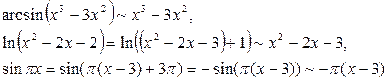
Получаем
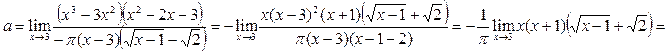
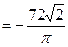 .
.
Пример 25. Вычислить предел функции 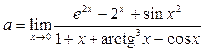 .
.
Решение. 1-й способ. Преобразуем исходное выражение и разделим числитель и знаменатель на х: 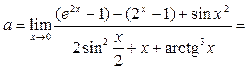
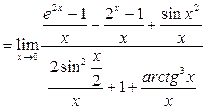 . Тогда по арифметическим свойствам предела
. Тогда по арифметическим свойствам предела 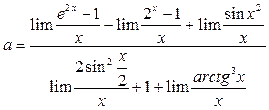 . По таблице заменяем выражения на эквивалентные и переходим к пределу в каждом слагаемом:
. По таблице заменяем выражения на эквивалентные и переходим к пределу в каждом слагаемом: 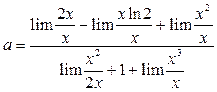
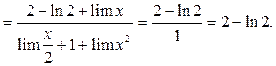
2-й способ. Поскольку 
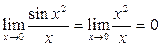 , то
, то  . Точно так же
. Точно так же 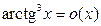 и
и 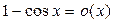 при
при 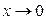 . Воспользовавшись этими соотношениями, получаем
. Воспользовавшись этими соотношениями, получаем
 .
.
Пример 26. Вычислить предел функции
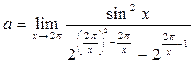 .
.
Решение. Вынесем в знаменателе исходного выражения множитель 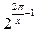 и учтём, что
и учтём, что 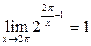 :
: 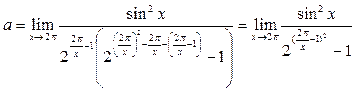 . Теперь сделаем замену переменной, воспользуемся формулой приведения и табличными эквивалентностями:
. Теперь сделаем замену переменной, воспользуемся формулой приведения и табличными эквивалентностями:
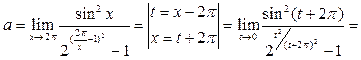
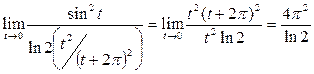 .
.
.
Пример 27. Вычислить предел функции 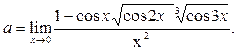
Решение. 1-й способ. Преобразуем числитель исходного выражения:
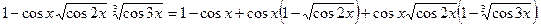
Используя последнее равенство, приём умножения на сопряжённое выражение, предел 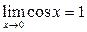 и табличные эквивалентности, получаем:
и табличные эквивалентности, получаем:
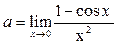 +
+ 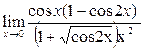 +
+ 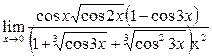 =
=
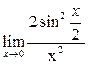 +
+ 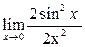 +
+ 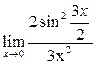 =
= 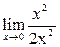 + 1 +
+ 1 + 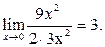
2-й способ. Последовательно используя табличные формулы
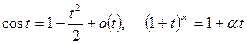 при
при 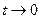 , получаем
, получаем
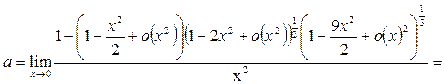

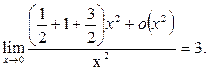
Пример 28. Вычислить предел функции 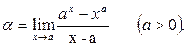
Решение.Сделаем подстановку  и воспользуемся табличными формулами:
и воспользуемся табличными формулами: 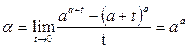
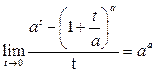
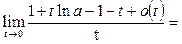
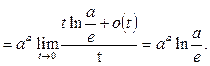
Пример 29. Вычислить предел функции 
Решение. Сделаем подстановку  :
:

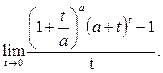 (10)
(10)
Преобразуем выражение 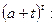
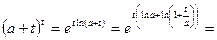
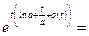

Подставляем полученное выражение в (10):
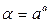
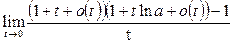
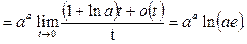
Пример 30. Вычислить предел функции 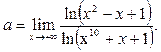
Решение. 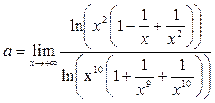
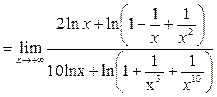
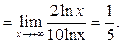
Мы воспользовались свойствами логарифма и тем, что 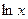 есть бесконечно большая, а
есть бесконечно большая, а 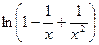 и
и 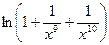 -бесконечно малые при
-бесконечно малые при 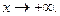
Пример 31. Найти предел 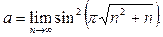
Решение. Понизим степень в исходном выражении и вынесем n из-под корня:  Теперь используем табличное представление
Теперь используем табличное представление 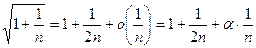 , где
, где 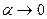 при
при 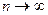 , формулу приведения и то, что
, формулу приведения и то, что 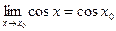 (непрерывность косинуса):
(непрерывность косинуса):
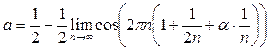
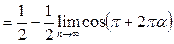
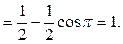
Пример 32.Вычислить предел функции
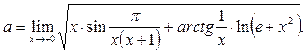
Решение.Величина 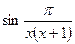 является ограниченной, а x - бесконечно малой при
является ограниченной, а x - бесконечно малой при 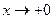 . Поэтому их произведение есть бесконечно малая. Далее,
. Поэтому их произведение есть бесконечно малая. Далее, 
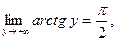 поэтому
поэтому 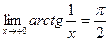 ;
; 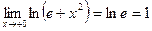 . Отсюда
. Отсюда 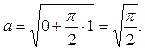
Пример 33.Вычислить предел функции 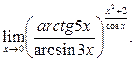
Решение.Воспользуемся тем, что если
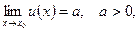
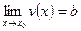 , то
, то 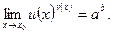 В нашем случае
В нашем случае 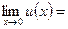
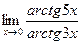 ,
, 
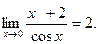 Тогда
Тогда 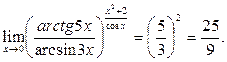
Задачи, связанные с применением второго замечательного предела
Второй замечательный предел
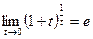 (11)
(11)
применяется ( как и в случае последовательностей) при вычислении пределов 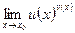 , где
, где 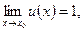
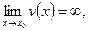 т.е. в случае неопределённости вида
т.е. в случае неопределённости вида 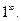
Следующие три примера решим различными способами.
Пример 34.Вычислить предел функции 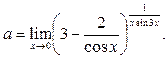
Решение. Находимпределы основания и показателя степени исходноговыражения и убеждаемся в том,что переднаминеопределённость вида 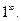 Выделяем в исходном выражении формулу
Выделяем в исходном выражении формулу 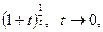 и вычисляем предел.
и вычисляем предел.
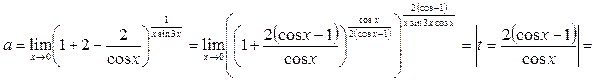
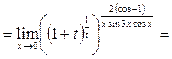
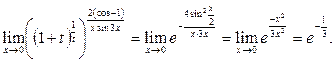
Предел выражения можно находить, предварительно вычислив предел его логарифма.
Пример 35.Вычислить предел функции 
Решение.Преобразуем логарифм исходного выражения, применив формулу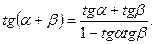
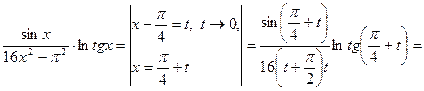
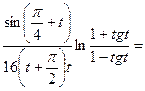
 Отсюда
Отсюда 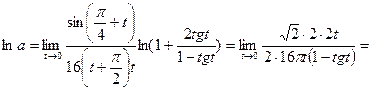
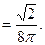 Теперь находим искомый предел:
Теперь находим искомый предел: 
Для вычисления предела 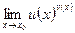 , где
, где 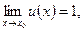
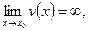 т.е. в случае неопределённости вида
т.е. в случае неопределённости вида 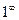 , можно использовать правило:
, можно использовать правило:
 . (12)
. (12)
Пример 36.Вычислить предел функции 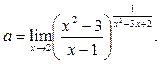
Решение.Находим
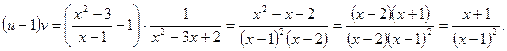
Далее, 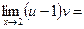
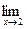
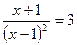 и в силу (12) получаем
и в силу (12) получаем 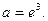
Пример 37.Последовательность функций  определяется следующим образом:
определяется следующим образом: 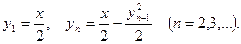 Найти
Найти 
Решение.Легко заметить и доказать по индукции, что 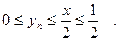 Оценим разность между
Оценим разность между 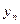 и числом
и числом 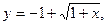 являющимся корнем уравнения
являющимся корнем уравнения 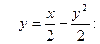
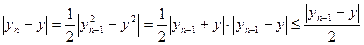 . Последнее неравенство следует из того, что
. Последнее неравенство следует из того, что 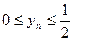 и
и 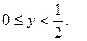 Применяя полученное неравенство
Применяя полученное неравенство 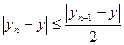 к разности
к разности 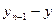 и т.д., получим
и т.д., получим 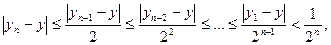 то есть
то есть 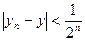 . Отсюда видно, что
. Отсюда видно, что 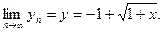
Непрерывность функции
Определение.Функция 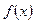 , заданная на множестве Е
, заданная на множестве Е 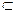 R, называется непрерывной в точке а
R, называется непрерывной в точке а 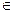 Е, если
Е, если
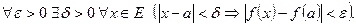 (13)
(13)
Отсюда следует, что в изолированной точке множества Е функция непрерывна (см. пример 41); если же а - предельная для множества Е, то (13) означает, что 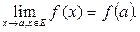
Пример 38.Доказать, чтофункция 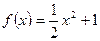 непрерывна в точке а=2(найти
непрерывна в точке а=2(найти 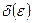 ).
).
Решение. 1-й способ.Поскольку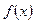 определена при всехзначениях
определена при всехзначениях  R,тоЕ= R и(13) принимает вид:
R,тоЕ= R и(13) принимает вид: 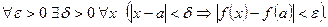
Переходим к неравенству для значений функции:
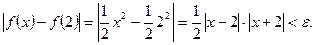 (14)
(14)
Пусть выполненонеравенство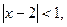 то есть
то есть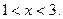 Тогда
Тогда 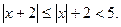 Если теперь потребовать, чтобы выполнялось неравенство
Если теперь потребовать, чтобы выполнялось неравенство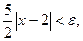
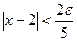 ,то неравенство (14) также будет выполнено:
,то неравенство (14) также будет выполнено: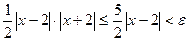 Итак, для выполнения последнего неравенствапотребовалось, чтобы
Итак, для выполнения последнего неравенствапотребовалось, чтобы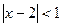 и
и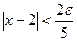 .Поэтому
.Поэтому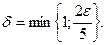
2-й способ.Неравенство  для значений функции выполнено, если выполнено неравенство
для значений функции выполнено, если выполнено неравенство
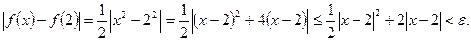
Последнее неравенство, (квадратное относительно  ) выполнено, если
) выполнено, если 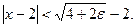 Таким образом,
Таким образом, 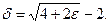
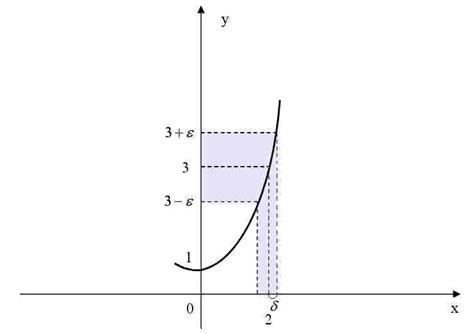
Рис.1
3-й способ.Найдём  по
по 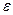 графически (см. рис. 1) и получим такой же результат, как для второго способа (в этом легко убедиться самостоятельно).
графически (см. рис. 1) и получим такой же результат, как для второго способа (в этом легко убедиться самостоятельно).
Пример 39.С помощью « 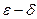 » рассуждений доказать непрерывность следующих функций: 1)
» рассуждений доказать непрерывность следующих функций: 1) 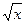 :2)
:2) 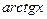 .
.
Решение.1).Пусть 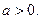 Тогда
Тогда 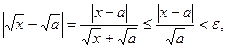 если
если 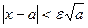 . Кроме того, должно выполняться условие
. Кроме того, должно выполняться условие 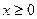 ,откуда
,откуда  и
и 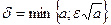 При а=0
При а=0 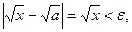 если
если 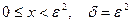 ( в качестве окрестности нуля в множестве Е=D(f)
( в качестве окрестности нуля в множестве Е=D(f) 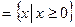 берётся
берётся  ).
).
2). Покажем, что для любых х и а
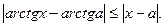 (15)
(15)
Из определения арктангенса и с помощью замены переменной получаем, что это неравенство равносильно неравенству
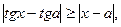 где
где  (16)
(16)
Если х и а одного знака, то