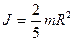Вращение вокруг неподвижной оси

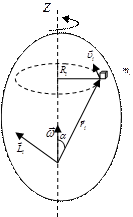Рассмотрим тело произвольной формы,

вращающееся вокруг оси Oz.

Разобьем его на элементарные массы .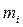

Для каждой из них можно записать

уравнение моментов с учетом моментов

внешних сил 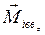и сил взаимодействия :

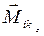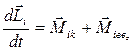
Запишем проекцию этого равенства на ось z:

Рис 15. Вращение вокруг

Момент импульса 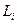связан со скоростью неподвижной оси

тела и его импульсом: 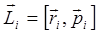. А при

вращательном движении его можно записать через угловую скорость, используя взаимосвязь 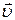и : 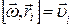. В результате получим: 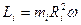, где 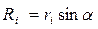(α – угол между радиусом вектором и осью z)

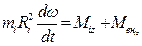
Величина 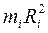называется моментом инерции (в данном случае i-той элементарной массы):

Далее просуммируем приведенное выше равенство по всему твердому телу:

.

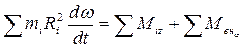Учитывая, что сумма моментов сил взаимодействия (внутренних) равна нулю, а угловое ускорение для всех точек одинаково, получим:

.

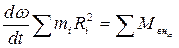И окончательно, уравнение динамики вращения твердого тела имеет вид:

,

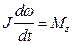где М_z проекция суммарного момента внешних сил на ось вращения, а

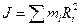- момент инерции твердого тела.

Момент инерции.

Приведенная выше формула для расчета инерции: 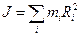- удобна для расчета момента инерции системы из нескольких тел, если эти тела можно считать материальными точками (случай, так называемых, дискретных масс). Но если мы хотим вычислить момент инерции твердого тела (непрерывное распределение масс) необходимо использовать операцию интегрирования:

.

Здесь dm - элементарная бесконечно малая масса, аналог m_i в предшествующем анализе.

Например, если стержень вращается вокруг одного из своих концов, момент инерции находим следующим образом: выделяем элементарную массу (бесконечно тонкий слой стержня толщиной dx) dm:

.

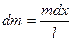Радиус вращения в данном случае обозначен x (смотри рисунок). Подставив dm и x вместо R в интеграл, получим:

.

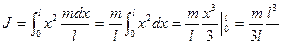
Здесь l -длина стержня, m-масса стержня.

Итак, момент инерции стержня относительно оси проходящей через один из его концов равен:

.

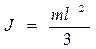Для того чтобы определить момент инерции стержня относительно оси, проходящей через его середину, надо изменить пределы интегрирования:

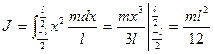
Момент инерции тела зависит от положения оси, относительно которой оно вращается.

Теорема Штейнера.

Теорема Штейнера позволяет сосчитать момент инерции J тела, имеющего массу m,относительно произвольной оси, если известен его момент инерции относительно центра масс J_c.

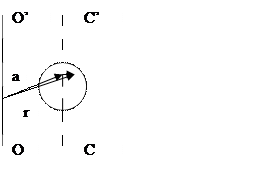Рассмотрим 2 оси: ось CC’ , проходящую через центр масс и произвольную OO’.

Положение элементарной массы задается вектором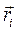

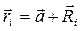
Момент инерции этой элементарной массы относительно оси OO’ будет равен:

Рис. 17. К теореме Штайнера. .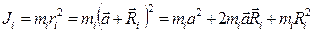

Просуммировав это равенство по всему

объему:

,

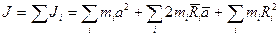и приняв во внимание, что для центра масс координата 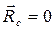, в итоге получим:

.

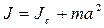Это соотношение называется теорема Штейнера, здесь a – расстояние от центра масс до оси OO’, относительно которой считается момент инерции.

Моменты инерции различных тел:

Момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню:

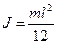
Момент инерции цилиндра или диска, относительно его оси:

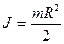
Момент инерции шара относительно его центра масс: