Определение стандартного отклонения

Как говорилось выше, чаще всего скорость счета препарата (образца) измеряют длительное время. В этом случае при статистической обработке результатов измерений пользуют­ся способом определения стандартного отклонения, основан­ным на законе распределения Пуассона.

Стандартным отклонениемназывается корень квадратный из общего числа набранных импульсов за единицу времени, то есть , где N — число набранных импульсов за единицу времени. Оно обычно обозначается σ и равно

,

но не стоит путать это с σ определяемой по методу наименьших квадратов. Это разные величины.

Скорость счета образца 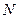будет равна

, (21)

где N — число импульсов за единицу времени, которое должно быть достаточ­но велико, так как в противном случае точность измерений будет невысокой.

Приведем несколько примеров: пусть насчитано 25 имп/мин, то есть N = 25. Тогда

,

а в процентах E= 20%. Эта ошибка довольно велика. Ос­тальные примеры приведены в табл. 4.

Как видно, при N ≥1000 имп/мин относительная ошибка будет удовлетворительно малой.

Таблица 4.Зависимость ошибки измерения от скорости счета образца

Значение N имп/мин	Скорость счета образца имп/мин	Относительная ошибка измерения	Ошибка измерения, %
	100±10	10 : 100=0,1	0,1×100=10
	1024±32	32: 1024=0,031	0,031×100=3,1
	2500±50	50 : 2500=0,02	0,02×100=2
	4225±65	65: 4225 = 0,015	0,015×100=1,5

Если число импульсов сосчитано за время t, то в едини­цу времени скорость счета образца будет в t раз меньше, то есть

или , (22)

где n— число импульсов, зарегистрированных за время t;

t — время измерения данного образца.

Формулу (22) можно записать по-другому:

(23)

где n/t — среднее арифметическое скорости счета;

— среднее стандартное отклонение отдельного из­мерения.

Очень часто при измерении скорости счета образца 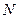нель­зя пренебречь значением скорости счета фона , тогда истин­ная скорость счета образца 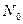определяется следующим обра­зом. Пусть имеем скорость счета образца+фон

,

и скорость счета фона

.

Тогда истинная скорость счета образца , причем общая ошибка определяется как корень квадратный из суммы квад­ратов стандартных отклонений для образца+фон и фона:

,(24) и (25)

Пример 3.При измерении фона в течение 50 минут бы­ло зарегистрировано 2500 импульсов, а при измерении об­разца в течение 30 минут — 3600 импульсов. Определить истинную скорость счета образца.

Решение.Скорость счетафона

(имп/мин)

В этом выражении величина 50, являясь средним арифме­тическим, представляет собой наиболее вероятную величину скорости счета фона, а величина 1 представляет собой среднее квадратичное отклонение при измерении скорости счета фона.

Скорость счета образца + фон будет

(имп/мин)

Величина 120 — наиболее вероятная величина скорости счета образца+фон, а величина представляет собой среднее квадратичное отклонение при измерении скорости счета образ­ца+фон.

Истинная скорость счета образца

(имп/мин)

будет находиться в пределах от 68 до 72 имп/мин.

Вычислим точность определения истинной скорости счета об­разца. Для этого определим относительную ошибку в про­центах:

. (26)

Степень точности, равная 3,1%, вполне удовлетворитель­ная, и поэтому можно считать измерения оконченными.