Основы теории косого резания грунта

Геометрические особенности косого резания

Косым резанием, называется резание грунта ножом, повернутым под углом 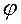в сторону от перпендикуляра, проведенного к направлению движения ножа (под углом 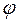в плане), в отличие от лобового, при котором режущая кромка ножа расположена перпендикулярно направлению движения.

Рассмотрим особенности данного вида резания. При повороте ножа в плане изменяются его геометрические параметры, влияющие на процесс резания. К таким параметрам относятся угол резания, длина ножа в направлении перемещения грунта и ширина резания.

Экспериментальными исследованиями Л.В. Красильникова установлено, что направление движения грунта по поверхности ножа при косом резании совпадает с направлением перемещения ножа. Это фиксировалось специальными флюгерными датчиками, установленными на поверхности рабочего органа, соприкасающейся с грунтом.

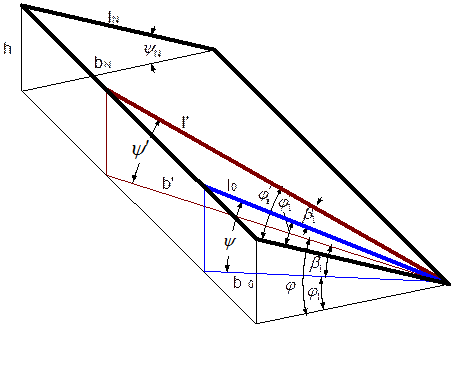
Рассмотрим нож (рис. 4.1), повернутый под углом 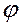в плане по отношению к его положению при лобовом резании, и определим необходимые параметры. Для их обозначения введем индекс “штрих”, а значение этих параметров будем называть текущими.

Из схемы видно, что

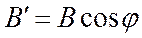. (4.1)

Из этой же схемы можно получить, что

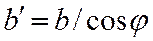, (4.2)

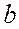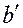где и - проекции на горизонтальную плоскость соответственно длины ножа 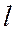и ее текущего значения 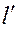, измеренного в направлении перемещения грунта.

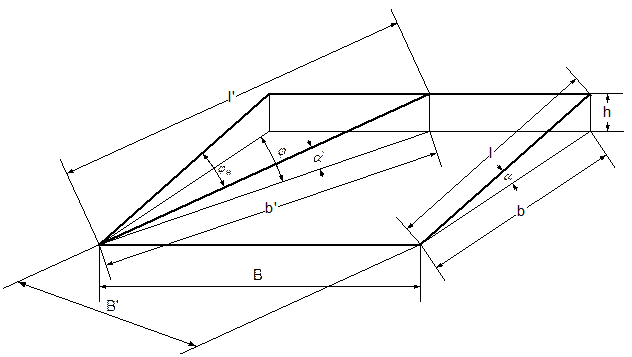Рисунок 4.1 – Схема для определения геометрических параметров ножа.

Кроме того, ясно, что

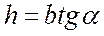, (4.3)

где 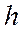– проекция на вертикальную плоскость длины ножа .

Тогда, с учетом уравнений (4.2) и (4.3), можно получить, что

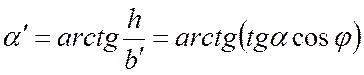. (4.4)

Определим текущее значение длины 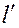следующим образом. Используя схему рис. 4.1, получим следующие уравнения

;

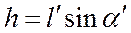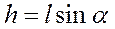(4.5)

Приравнивая првые части этих уравнений, получим, что

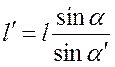. (4.6)

Таким образом, текущие значения геометрических параметров ножа выражены через их действительные значения при лобовом резании и угол 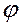поворота ножа в плане.

Отметим, что угол 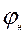, измеренный в плоскости ножа, можно найти, используя уравнения (4.5)

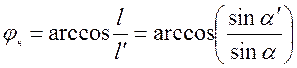. (4.7)

Рассмотрим площадку сдвига и аналогичным образом выведем зависимости, необходимые для дальнейших расчетов (рисунок 4.2).

Рисунок 4.2 – Схема площадки сдвига.

Используем аналогичные обозначения для длины площадки сдвига и – для ее проекции на чертежную плоскость с соответствующими индексами. Для параметров, измеренных в плоскости, совпадающей с направлением движения ножа и перпендикулярной поверхности разрабатываемого грунта, оставим в обозначениях индекс ”штрих”. Параметры, измеренные в плоскости, нормальной как к поверхности разрабатываемого грунта, так и к режущей кромке ножа, будем обозначать индексом ”N”. И, наконец, обозначения параметров измеренных в плоскости, совпадающей с направлением сдвига грунта по площадке скольжения, и по-прежнему нормальной поверхности разрабатываемого массива грунта, используем индексы “0”.

Отметим также, что величиной h на рисунке 4.2 обозначена толщина срезаемой стружки.

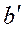Поскольку угол поворота ножа в плане является углом между отрезками и 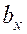, введем обозначение 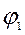для измерения угла между направлением, нормальным к режущей кромке и направлением, совпадающим с направлением сдвига грунта по площадке скольжения. Этот угол измеряется между отрезкам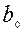и и 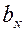. Угол между отрезкам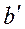и и 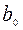обозначим, как 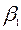. Значение 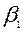дает величину угла между направлением, совпадающим с направлением сдвига грунта по площадке скольжения и направлением движения ножа. Таким образом, эти углы, измеряемые в горизонтальной плоскости, связаны между собой соотношением

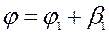. (4.8)

Аналогичные углы, измеренные между отрезкам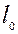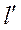и , и 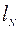в плоскости, совпадающей с площадкой сдвига, связаны между собой следующим образом

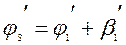. (4.9)

Выведем соотношение между величинами приведенных выше углов, приняв за основу угол 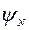. Из схемы видно, что

;

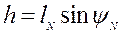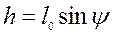; (4.10)

.

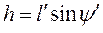а также, что

;

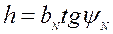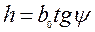; (4.11)

.

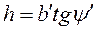Справедливы также следующие соотношения между отрезкам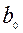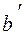и , и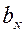

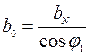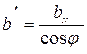; , (4.12)

и соотношения между отрезкам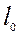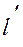и , и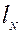

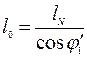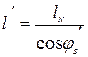; . (4.13)

Из схемы (рисунок 4.2) и уравнений (4.11) и (4.12) можно получить, что

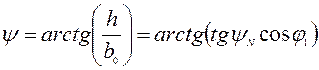, (4.14)

а также, что

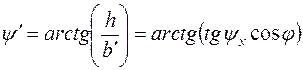. (4.15)

Из уравнений (4.13) и (4.10) и той же самой схемы получим после преобразований величину угла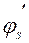

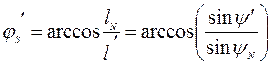, (4.16)

а также величину угла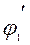

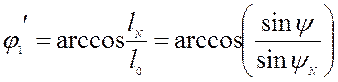. (4.17)

Таким образом, получены все основные соотношения между углами и отрезками, необходимыми при дальнейших расчетах.

Перейдем к определению массы грунта, перемещаемой по ножу. Будем рассматривать резание при относительно длинном ноже, высоты H которого достаточно, чтобы срезанный грунт свободно пересыпался через верхнюю кромку ножа. В противном случае поток грунта будет перемещаться не только по ножу, но и по грунту, расположенному за ножом (рисунок 4.3). Такая расчетная схема имеет свои особенности, заключающиеся в том, что в движении находится несколько большее количество грунта, чем это обеспечивается высотой ножа. Это приводит к некоторому увеличению сопротивления резанию. Ограничение на высоту ножа будет иметь вид

Рисунок 4.3 – Резание грунта ножом малой высоты.

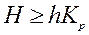, (4.18)

где 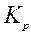– коэффициент разрыхления грунта.

Это ограничение появляется из-за увеличения грунтом своего объема при разработке, характеризуемого коэффициентом .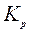

Повернем типовой нож на угол 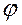в плане и рассмотрим особенности отделения грунта от массива и движения его по ножу в этом случае.

Допустим, что при каком-то положении ножа от грунта отделится элемент с поверхностью О'С'С₁'О₁' (рисунок 4.4). При дальнейшем перемещении ножа в направлении 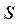в массив ненарушенной структуры внедряются сразу две кромки ножа - нижняя и боковая, лидирующая по ходу движения и находящаяся в грунте кромка, являющаяся продолжением отрезка К₁С₁. В какой-то момент отделится новый элемент стружки с поверхностью ОСС₁О₁ – произойдет новый сдвиг. Следовательно, при сдвиге преодолевается сцепление грунта как по всей площадке сдвига, формирующейся перед ножом по его длине и выходящей на поверхность грунта на отрезке ОО₁, так и по всей торцевой площадке сдвига перед лидирующей боковой режущей кромкой, выходящей на поверхность грунта на отрезке О₁С₁.

На части второй торцевой площадки у ведомой режущей кромки сцепление между частичками грунта было разрушено при предыдущих сдвигах. На оставшейся части площадки сцепление разрушается при формировании нового сдвига.

Отметим, что сдвиг грунта может произойти под некоторым углом 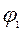по отношению к перпендикуляру, проведенному к режущей кромке. Это происходит из-за того, что силы трения, действующие со стороны ножа на отделяемый элемент грунта и на грунт, перемещающийся по ножу, направлены в сторону движения. Поэтому и сдвиг грунта может произойти с отклонением от нормали в ту же сторону, куда движется нож, что вытекает из условий равновесия отделяемого элемента грунта.

Рассмотрим движение грунта по ножу, также имеющее свои особенности. Прежде всего, отметим, что при движении грунта по поверхности ножа происходит смещение элементов стружки грунта как вверх по ножу, так и одновременно вдоль ножа.

Поэтому часть лобовой поверхности ножа у лидирующей боковой режущей кромки остается свободной от грунта (область С₁К₁К₁' на рисунок 4.4). Другая часть, соответствующая отрезку С₁О₁ ножа, заполнена наполовину, так как толщина грунта на ноже вдоль отрезка О₁К' такая же, как и на остальной части ножа, а вдоль отрезка С₁К₁' равна нулю. При этом следует иметь в виду, что при увеличении длины ножа (отрезки СК и С₁К₁) незаполненная грунтом лобовая площадь ножа увеличивается.

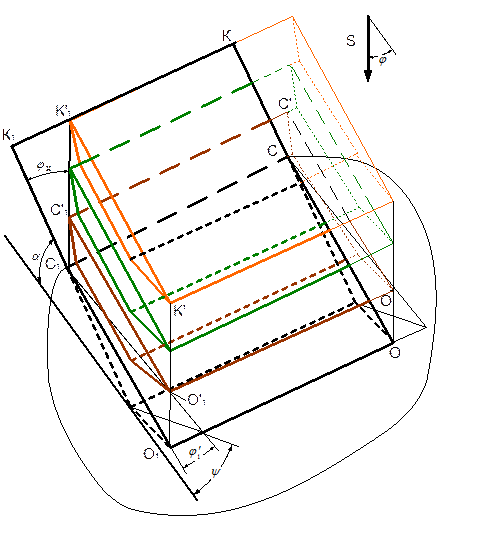Рисунок 4.4 – Схема разрушения грунта.

Из этих рассуждений можно сделать вывод о том, что эффективность косого резания должна повышаться при увеличении высоты ножа из-за относительного уменьшения объема перемещаемого грунта.

Достигнув верхней кромки ножа на отрезке КК₁', грунт пересыпается через нож. Такое же явление происходит и вдоль ведомой боковой кромки ножа.

Таким образом, в отделении грунта от массива участвуют нижняя и лидирующая боковая кромка ножа. Грунт сходит с ножа частично через верхнюю кромку и частично через ведомую боковую кромку. При достаточно большой высоте ножа весь грунт может сходить с него через ведомую режущую кромку.

Составим расчетную схему для определения веса грунта, перемещающегося по ножу в направлении 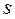, с учетом отмеченных выше особенностей (рисунок 4.5).

Объем грунта, срезаемый режущей кромкой ножа, представляет собой объем параллелепипеда с нижним ОВВ₁О₁ и верхним Д₀К₀К'Д' основаниями. В плоскости, нормальной режущей кромке ножа, нижнее основание расположено под углом 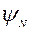к грунту. Примем допущение, что пересыпание грунта через верхнюю кромку будет осуществляться по такой же площадке.

Найдем объем рассматриваемого параллелепипеда.

Площадь параллелограмма ВК₀К'В₁ будет равна площади поверхности рабочего органа.

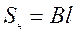. (4.19)

Толщина рассматриваемого параллелепипеда 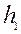определится из схемы на рисунок 4.5 следующим образом

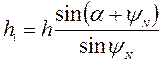. (4.20)

Тогда объем параллелепипеда будет равен

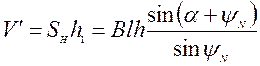. (4.21)

Часть объема параллелепипеда, расположенная вне ножа, будет осыпаться по ведомой боковой кромке ножа (отрезок КВ). Можно принять для определенности допущение, что осыпание грунта по ведомой грани (отрезок КВ на рисунке 4.5) будет происходить в вертикальной плоскости.

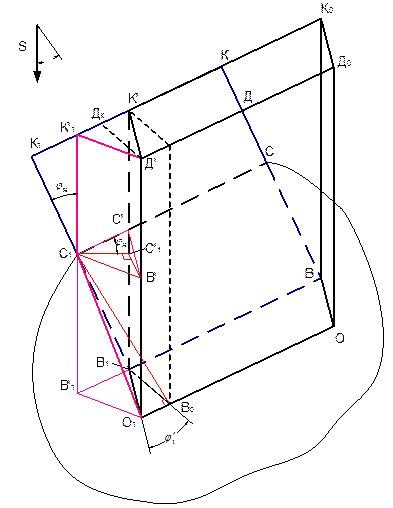а)

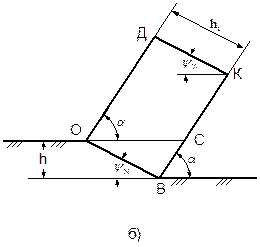Рисунок 4.5 – Схема для расчета объема грунта, перемещаемого по ножу (а); поперечное сечение грунта (б).

В этом случае отсекаемый отрезком КВ объем грунта при условном его перемещении на свободную поверхность ножа (без учета треугольной призмы грунта с основанием Д'К'К'₁) полностью заполняет ее. Объем грунта, реально перемещающейся по ножу можно представить таким образом

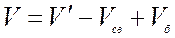(4.22)

где V_св – объем части параллелепипеда, осыпающийся через ведомую боковую кромку; V_б – объем треугольной призмы грунта, срезаемый лидирующей боковой кромкой.

Объем осыпающийся части параллелепипеда определим исходя из свободной поверхности ножа К'К₁В₁, которую необходимо корректировать с учетом того, что сдвиг грунта происходит под углом 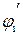, измеренным в плоскости площадки сдвига.

Длину отрезка К'Д_к,, равную длине отрезка В₀О₁, с учетом схемы на рисунке 4.2, можно найти следующим образом

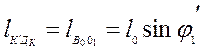, (4.23)

где значения 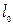и 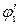принимаются по уравнениям (4.13) и (4.17).

Учитывая, что

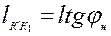, (4.24)

объем V_св найдем из формулы

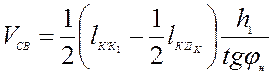. (4.25)

При пользовании формулой (4.25), в нее необходимо подставлять значения величин из уравнений (4.20), (4.23) и (4.24).

Перейдем к определению объема V_б призмы грунта, срезаемого боковой кромкой. Продлим отрезок К₁'С₁ до точки В₁' так, чтобы призма с основаниями К'К'₁Д' и В₁В₁'О₁ стала полной. Отметим при этом, что объем пирамиды В₁В'₁О₁С₁, дополняющий призму с боковым ребром В₁С' до полной, составляет 1/3 ее объема.

Тогда можно написать, что

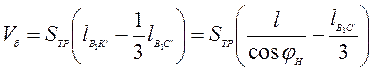, (4.26)

где S_ТР- площадь перпендикулярного сечения призмы.

Найдем длину отрезка В₁С' и площадь S_ТР. Из схемы на рис. 4.5 видно, что отрезок В₁С₁ равен отрезку ВС, тогда

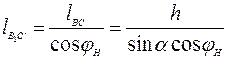, (4.27)

Из этой же схемы можно получить, что

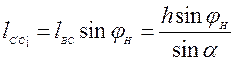. (4.28)

Высота перпендикулярного сечения, имеющая треугольную форму, равна толщине параллелепипеда h₁ (уравнение 4.20).

Тогда

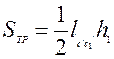. (4.29)

Подставляя полученные значения 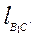(уравнение 4.27) и S_ТР (уравнение 4.29) в уравнение (4.26), определим объем грунта, срезаемый лидирующей боковой кромкой и перемещающийся по ножу.

Рассмотренный выше случай движения грунта предполагал, что часть грунта пересыпается через верхнюю кромку. При совмещении точки К’ с точкой К, через верхнюю кромку ножа будет пересыпаться только грунт, срезаемый лидирующей боковой кромкой.

При выполнении условия

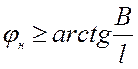(4.30)

грунт, срезаемый лобовой кромкой, будет пересыпаться только через боковую кромку.

Рассмотрим случай, когда весь срезаемый грунт пересыпается через боковую кромку ножа (рисунок 4.6).

Поступим следующим образом. Будем рассматривать условную длину ножа l_ус, представленную на рисунке 4.6 отрезком BK’. Точка К’ является точкой пересечения отрезка В₁К’ с ведомой боковой кромкой ножа ВК. Если длина ножа будет равна условной длине, то грунт, срезаемый лидирующей боковой кромкой, будет пересыпаться через верхнюю кромку, а грунт, срезаемый лобовой кромкой – через ведомую боковую. Величину условной длины ножа можно найти из соотношения

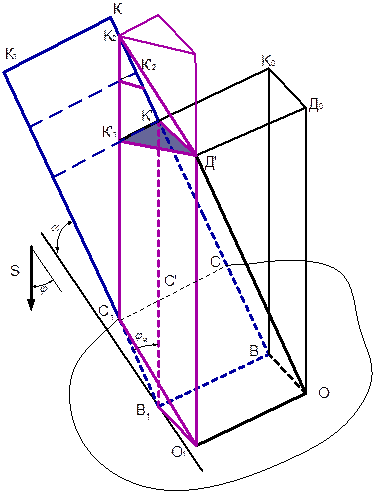Рисунок 4.6 – Схема для определения объема грунта, перемещаемого по ножу при условии, что весь грунт сходит через ведомую боковую кромку.

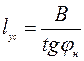. (4.31)

Подставляя полученное значение l_ус в уравнение (4.21) вместо значения l, получим объем условного параллелепипеда.

Поступая аналогичным образом с уравнением (4.24) и уравнением (4.25), куда входит измененное значение 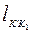, получим величину объема 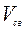. Отметим, что при l= l_ус уравнение (4.24) дает численные значения ширины ножа.

Перейдем к определению объема 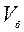, срезаемого боковой кромкой ножа. Если площадь 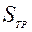и длина отрезка В₁С’ не изменяется, и по-прежнему будут определяться по уравнениям (4.29) и (4.27), то уравнение (4.26) необходимо корректировать.

Рассмотрим случай, когда весь грунт, срезаемый лидирующей боковой кромкой, пересыпается через ведомую боковую кромку. Длина отрезка К’К₂ при этом равна длине отрезка В₁С₁ (ВС). Рассматриваемый случай существует при выполнении условия (4.30) и дополнительно условия

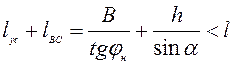. (4.32)

С достаточной степенью точности можно принять, что объем оставшейся на ноже части призмы равен ½ объема полной призмы с длиной бокового ребра К₂К’₁, которая будет равна длине отрезка В₁С’ (уравнение 4.27).

Тогда, обозначив для этого случая объем грунта, срезаемый лидирующей боковой кромкой через 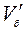, получим

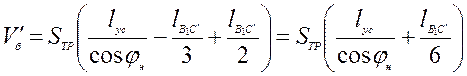. (4.33)

Если условие (4.30) выполняется, а условие (4.32) не выполняется, то в этом случае часть грунта, срезаемого боковой кромкой пересыпается через верхнюю кромку ножа, а часть – через ведомую боковую. Поступим в этом случае следующим образом. Примем, что верхняя кромка ножа проходит через точку 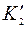(рисунок 4.6).

Длина отрезка 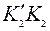в том случае, когда условие (4.32) не выполняется, будет равна

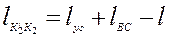. (4.34)

Примем допущение, что площади основания усеченной пирамиды 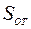, образуемой грунтом в верхней части ножа, и площадь перпендикулярного сечения призмы 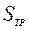связаны с длиной отрезков 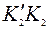и 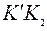, равным длине отрезка ВС, соотношением

,

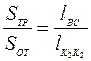откуда получим величину объема отсекаемой верхней кромкой пирамиды

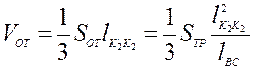. (4.35)

Тогда , для рассматриваемого случая

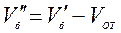, (4.36)

где 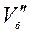– объем оставшейся на ноже призмы грунта, срезанного лидирующей боковой кромкой.

Таким образом, объем грунта, перемещаемого по ножу при косом резании, определяется по следующему алгоритму. Если условие (4.30) не выполняется, то используем формулу (4.22), а для определения значений V^’, V_св и V_б используем формулы (4.21), (4.25) и (4.26).

Если условие (4.30) выполняется и при этом выполняется условие (4.32), то весь срезаемый грунт пересыпается через ведомую боковую кромку. В этом случае при определении значений V^’ и V_св вместо длины ножа l в соответствующих формулах необходимо использовать условную длину l_ус, значение которой определяется по уравнению (4.31). Кроме этого, вместо величины V_б следует подставлять величину объема V_б’, полученную по уравнению (4.33).

Если условие (4.30) выполняется, а условие (4.32) не выполняется, по-прежнему используется формула (4.22). Значения V^’ и V_св определяются с использованием условной длины l_ус, как и в предыдущем случае. Вместо значения V_б следует подставить значение 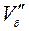, получаемое по уравнению (4.36).

В заключение определим площадь лобовой площадки сдвига ОВВ₁О₁. В соответствии с рисунком 4.2 имеем

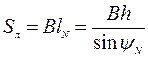. (4.37)

Так как отрезок l_N расположен в плоскости, нормальной к режущей кромке и является высотой поверхности ОВВ₁С₁ при ее ширине, равной ширине ножа В.