Десятичная запись приближенных чисел
Введение
Решение научно-технической задачи состоит из следующих этапов:
- анализ постановки задачи;
- формальное моделирование решения задачи;
- практическое решение.
Этап формального моделирования представляет собой решение поставленной (научно-технической) задачи в виде математической задачи, являющейся ее моделью. Для решения математических задач используются методы:
- графические;
- аналитические;
- численные .
Графические методыпозволяют в ряде случаев оценить порядок искомой величины. Основная идея этих методов состоит в том, что решение находится путем геометрических построений. Например, для нахождения корней уравнения 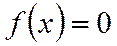 строится график функции
строится график функции  , координаты точек пересечения которого с осью абсцисс и будут искомыми корнями.
, координаты точек пересечения которого с осью абсцисс и будут искомыми корнями.
При использовании аналитических методов решения задачи удается выразить с помощью формул. В частности, если математическая задача состоит в решении простейших алгебраических или трансцендентных уравнений, дифференциальных уравнений и т.п., то использование известных из курса математики приемов сразу приводит к цели. К сожалению, на практике это слишком редкие случаи.
Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами (другими словами алгоритму). Результаты при этом получаются в виде числовых значений.
Численные методы анализа необходимы в случаях, когда точное решение задачи или не может быть получено или его использование затруднительно из-за громоздкости и представляют собой приближенные методы решения задач. Многие численные методы разработаны давно, однако при вычислении вручную они могли использоваться лишь для решения не слишком трудоемких задач. С появлением ЭВМ начался период бурного развития численных методов и их внедрения в практику.
Численные методы компьютерного анализа – это приближенные методы решения задачи с использованием ЭВМ с целью получения результата за приемлемое время.
Численные методы разрабатывают и исследуют, как правило, высококвалифицированные специалисты-математики. Что касается подавляющей части студентов инженерных специальностей, то для них, т.е. для нас, главными задачами являются:
- понимание основных идей методов особенностей и областей их применения;
- умение выбрать из имеющегося арсенала методов тот, который наиболее пригоден в данном конкретном случае.
Основная литература
1. Демидович Б.П., Марон И.А. Основы вычислительной математики.
2. Демидович Б.П., Марон И.А. Численный анализ.
3. Краскевич В.Е., Зеленский К.Х. Численные методы в инженерных исследованиях.
4. Бахвалов Н.С. Численные методы.
Теория приближенных чисел
( Теория погрешностей)
Основные понятия и определения
Определение. Приближенным числом  называется число, незначительно отличающееся от точного (истинного) А и заменяющее последнее в вычислениях. Если известно что
называется число, незначительно отличающееся от точного (истинного) А и заменяющее последнее в вычислениях. Если известно что  , то
, то 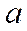 называется приближенным значением числа А по недостатку, если
называется приближенным значением числа А по недостатку, если 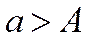 , то – по избытку.
, то – по избытку.
Определение. Под ошибкой(погрешностью) 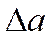 приближенного числа
приближенного числа 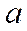 обычно понимается разность между соответствующим точным числом А и данным приближением.
обычно понимается разность между соответствующим точным числом А и данным приближением.
 (1.1)
(1.1)
Если  , то
, то  - положительная,
- положительная,  ,
,
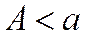 то
то  - отрицательная,
- отрицательная, 
Из (1.1) следует, что
 (1.2)
(1.2)
Т.о., точное число можно рассматривать как приближенное с ошибкой равной 0.
Определение. Абсолютной погрешностью 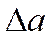 приближенного числа
приближенного числа  называется абсолютная величина разности между соответствующим точным числом А и приближенным числом
называется абсолютная величина разности между соответствующим точным числом А и приближенным числом 
 (1.3)
(1.3)
Следует различать два случая:
1. Число А нам известно, тогда 
легко определяется по формуле (1.3).
2.Число А нам неизвестно, что практически
бывает чаще всего, и, следовательно, мы не можем определить  по формуле (1.3).
по формуле (1.3).
В этом случае полезно вместо неизвестной теоретической абсолютной погрешности  ввести ее оценку сверху, т.н. предельную абсолютную погрешность.
ввести ее оценку сверху, т.н. предельную абсолютную погрешность.
Определение. Под предельной абсолютной погрешностью 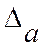 , или
, или  понимается всякое число, не меньшее абсолютной погрешности этого числа
понимается всякое число, не меньшее абсолютной погрешности этого числа
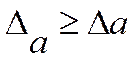 (1.4)
(1.4)
Заметим, что сформулированное выше понятие предельной абсолютной погрешности является весьма широким, а именно: под предельной абсолютной погрешностью приближенного числа  понимается любой представитель бесконечного множества не отрицательных чисел, удовлетворяющих неравенству (1.4).
понимается любой представитель бесконечного множества не отрицательных чисел, удовлетворяющих неравенству (1.4).
Абсолютная погрешность (или предельная) абсолютная погрешность не достаточна для характеристик точности (качества) измерения или вычисления. Для характеристики точности используют абсолютною погрешность, приходящуюся на единицу длины, которая называется относительной погрешностью.
Определение. Относительной погрешностью  приближенного числа называется отношение абсолютной погрешности
приближенного числа называется отношение абсолютной погрешности  этого числа к модулю соответствующего точного числа А , при
этого числа к модулю соответствующего точного числа А , при
этом 
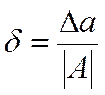 (1.5)
(1.5)
Так же как и для абсолютной погрешности и по тем же причинам, введем понятие предельной относительной погрешности.
Определение. Предельной относительной погрешностью  приближенного числа называется всякое число, не меньше относительной погрешности этого числа
приближенного числа называется всякое число, не меньше относительной погрешности этого числа 
 (1.6)
(1.6)
Основные источники погрешностей:
- погрешности задачи – погрешности, связанные с постановкой задачи, а также принятые нами при изучении тех или иных явлений условия, упрощающие задачу;
- погрешности математических методов – погрешности, связанные с наличием бесконечных последовательностей (рядов) в математическом анализе;
- неустранимые погрешности – погрешности исходных данных, в том числе и физических, математических констант;
-погрешности окружения – погрешности, связанные с системой исчисления;
- погрешности действий – погрешности, связанные с действиями над приближенными значениями.
Само собой разумеется, что при решении
конкретной задачи те или иные погрешности
иногда отсутствуют или влияние их ничтожно.
Мы ограничимся в данном разделе исчислением погрешностей чисел и арифметических действий.
Десятичная запись приближенных чисел
Всякое положительное число 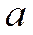 может быть представлено в виде конечной или бесконечной десятичной дроби
может быть представлено в виде конечной или бесконечной десятичной дроби
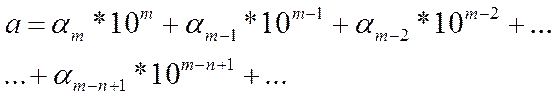 (1.7)
(1.7)
Где 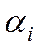 - цифры числа
- цифры числа  ,
,
 ,
,
 - некоторое целое число (старший десятичный разряд числа
- некоторое целое число (старший десятичный разряд числа 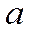 )
)
Определение. Значащей цифрой приближенного числа называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он находится между значащими цифрами.
Нуль в начале и конце числа имеет различные значения:
- нули, стоящие в начале чисел, до цифр отличных от нуля, не являются значащими;
- нули, которые стоят в конце числа, после последней цифры отличной от нуля, имеют двойной смысл:
1. 1кг = 1000г – в этом случае имеет место точное соотношение и поэтому все нули в таких соотношениях – значащие цифры;
2. Население бывшего Советского Союза 280.530.000 человек – в этом случае нули стоят вместо неизвестных цифр и в таких случаях – нули незначащие цифры. Для того чтобы избежать недоразумений, никогда не следует писать нули вместо неизвестных цифр, лучше всего принять такую форму записи числа 28053*104 или 2,8053*108, т.к. нули в конце этого числа только определяют его порядок.
Определение. Говорят, что  первых значащих цифр (десятичных знаков) приближенного числа являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого
первых значащих цифр (десятичных знаков) приближенного числа являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого  значащей цифрой, считая слева направо
значащей цифрой, считая слева направо
 (1.8)
(1.8)
или являются верными в широком смысле, если
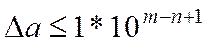 (1.9)
(1.9)
Если положительное приближенное число 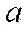 имеет
имеет  верных десятичных знаков в узком смысле
верных десятичных знаков в узком смысле 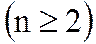 , то
, то
 (1.10)
(1.10)
или в широком смысле
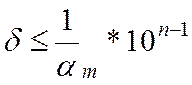 (1.11)
(1.11)
Точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр. В тех случаях, когда приближенное число содержит излишнее число неверных цифр прибегают к округлению.
Округление проводят так, чтобы погрешность округления была минимальной. Для этого придерживаются следующего правила округления: если первая из отбрасываемых цифр меньше пяти, то все оставляемые цифры не изменяют, если больше или равна пяти, то последнюю оставшуюся цифру увеличивают на единицу.
Если при округлении числа оставляют значащих цифр на одну больше, чем верных, то эта оставленная цифра называется сомнительной.
