II. Выполнение измерений и обработка результатов
Лабораторная работа № 10.
Определение скорости звука в воздухе методом стоячих волн.
Оборудование:трубка Кундта с поршнем, камертон, линейка, молоточек (стержень).
I. Основные понятия и определения.
Колебания, лежащие в интервале от 20 до 20000 Гц, обладают свойством вызывать ощущение звука и могут быть выделены по этому признаку в особую группу звуковых или акустических колебаний, называемых звуком.
Процесс распространения колебаний, называемый волной, в зависимости от угла между направлением колебаний частиц и распространением волны может быть поперечным или продольным. В твёрдых телах могут распространяться как те, так и другие волны, а в жидкостях и газах – только продольные.
Математически уравнение волны (как поперечной, так и продольной) определяет величину смещения колеблющейся точки S в зависимости от времени и координат относительно положения равновесия х.
Пусть точка О участвует в гармоническом колебательном движении с амплитудой α и круговой частотой ω. Тогда смещение её от положения равновесия x можно описать уравнением:
S(x)=αcosωt, (10.1)
где α – амплитуда волны.
Колебания, распространяясь в среде, дойдут до точки A, лежащей на расстоянии х от точки O, через время:
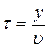 , (10.2)
, (10.2)
где 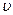 - скорость распространения волны.
- скорость распространения волны.
Если волна идёт, не затухая, то смещение точки A определяется по формуле (10.1), но в новый момент времени t’= t- 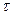 :
:
S(x)=αcosω(t- 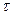 ).
). 
Учитывая (10.2), получим:
S(x)=αcosω(t - 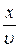 ). (10.3)
). (10.3)
Выражение (10.3) представляет собой искомое уравнение плоской волны, распространяющейся вдоль прямой OA.
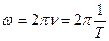 ,
,
где 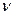 - частота; Т - период колебаний, можно записать:
- частота; Т - период колебаний, можно записать:
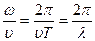 ,
,
где 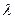 - длина распространяющейся волны.
- длина распространяющейся волны.
Тогда выражение (10.3) может быть преобразовано к виду:
S(x)=αcos(ωt-2 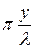 )
)
или
S(x)=αcos(ωt-2 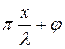 ), (10.4)
), (10.4)
где S(х) - смещение колеблющейся точки; α - амплитуда колебаний; 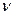 - частота колебания; t – время; x - расстояние колеблющейся точки от источника колебания;
- частота колебания; t – время; x - расстояние колеблющейся точки от источника колебания; 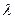 - длина волны,
- длина волны, 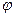 - начальная фаза волны, Ф(x, t)=
- начальная фаза волны, Ф(x, t)= 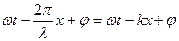 , полная фаза волны,
, полная фаза волны, 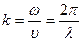 - волновой вектор.
- волновой вектор.
Любую волну характеризуют три основные величины: длина волны 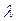 , скорость распространения
, скорость распространения 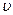 и частота
и частота 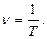 Так как
Так как 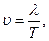 то
то
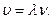
Рассмотрим простой случай интерференции двух волн одинаковой частоты, длины и амплитуды, распространяющихся в противоположных направлениях. На опыте это можно осуществить, если на пути бегущей волны перпендикулярно к направлению распространения поставить хорошо отражающую преграду. В результате интерференции волны падающей и волны отражённой возникнет так называемая стоячая волна.
Падающая волна, распространяющаяся по направлению оси у на основании (10.4), определяется уравнением:
S1(х1)=αcos2 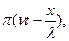
а уравнение отражённой волны:
S2(х1)=αcos2 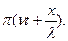
Тогда уравнение стоячей волны получим при сложении бегущей и отражённой волн:
S 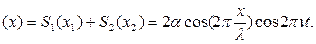
В уравнении стоячей волны по аналогии с бегущей волной множитель, не зависящий от времени, 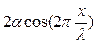 выражает амплитуду A результирующего колебания:
выражает амплитуду A результирующего колебания:
А= 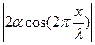 . (10.5)
. (10.5)
Из равенства (10.5) следует, что амплитуда стоячей волны зависит от координаты  колеблющейся точки. Так как функция
колеблющейся точки. Так как функция 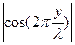 может принимать значения в пределах от 0 до 1, то точки в стоячей волне, для которых
может принимать значения в пределах от 0 до 1, то точки в стоячей волне, для которых
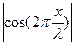 =1, (10.6)
=1, (10.6)
будут иметь наибольшую амплитуду А=2α.
Такие точки стоячей волны называются пучностями. Их координаты определяются из условия (10.6):
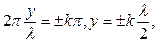 (10.7)
(10.7)
где k=0, 1, 2, 3…
Точки, для которых 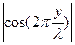 , имеют амплитуду, равную нулю, т.е. они не смещаются. Эти точки называются узлами стоячей волны.
, имеют амплитуду, равную нулю, т.е. они не смещаются. Эти точки называются узлами стоячей волны.
Их координаты:
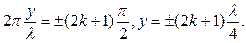 (10.8)
(10.8)
Из соотношений (10.7) и (10.8) следует, что расстояние между соседними узлами (соседними пучностями) в стоячей волне равно 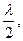 расстояние между пучностью и соседним узлом равно четверти длины волны
расстояние между пучностью и соседним узлом равно четверти длины волны 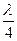 .
.
Стоячая волна фактически представляет собой совокупность бесконечного числа колебаний частиц среды одной и той же частоты 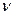 , но с различными амплитудами, причём смещение любой колеблющейся точки удовлетворяет уравнению:
, но с различными амплитудами, причём смещение любой колеблющейся точки удовлетворяет уравнению:
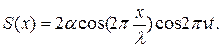
Рассмотрим несколько примеров колебания сплошных систем. Если струну, закреплённую на обоих концах, оттянуть, а затем отпустить, то в ней возникнут колебания, называемые собственными колебаниями струны. Эти колебания можно рассматривать как установившуюся в струне стоячую волну, полученную при наложении волны, бегущей вдоль струны, и волны, отражённой от её зажатого конца. На границах в данном случае образуются узлы. Это объясняется тем, что волна, отражаясь от более плотной среды, в месте отражения меняет свою фазу на противоположную. Тогда у границы складываются колебания противоположных направлений, что и ведёт к образованию узла. Значит, на всей длине струны 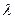 между двумя узлами уложится или половина длины волны
между двумя узлами уложится или половина длины волны 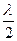 , или целая волна
, или целая волна 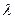 , или
, или 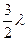 и т.д.
и т.д.
Следовательно, в струне могут возникнуть стоячие волны, длина которых удовлетворяет условию:
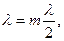
где m=0, 1, 2, 3…
Подобным образом можно рассматривать собственные колебания столба воздуха, как стоячие волны, заключённого в трубе с открытыми концами. В этом случае на концах образуются пучности стоячей волны, так как, отражаясь от менее плотной среды, волна не меняет фазы в месте отражения.
Как и в предыдущем случае, на всей длине столба воздуха между двумя пучностями уложится или 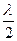 , или
, или 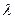 , или
, или 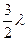 и т.д., т.е. в воздухе возникают стоячие волны, длина которых удовлетворяет условию:
и т.д., т.е. в воздухе возникают стоячие волны, длина которых удовлетворяет условию:
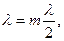
где m=0, 1, 2, 3… 
В системах с неодинаковыми условиями отражения волн на концах, например, в воздушном столбе трубы, закрытой только у одного конца, также можно возбудить собственные колебания. Но стоячие волны, соответствующие им, имеют на открытом конце пучность, а на закрытом – узел стоячей волны.
И на всей длине столба воздуха 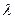 уложится или
уложится или 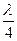 , или
, или 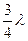 , или
, или 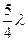 и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию
и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию
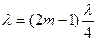 , (10.9)
, (10.9)
где m=0, 1, 2, 3… 
Случай возникновения собственных колебаний в столбе воздуха используют для нахождения скорости распространения звука в воздухе; 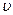 можно определить, зная длину звуковой волны
можно определить, зная длину звуковой волны 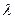 , распространяющейся от источника колебаний частоты
, распространяющейся от источника колебаний частоты 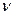 :
:
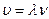 . (10.10)
. (10.10)
Для измерения длины волны используется явление акустического резонанса, т.е. усиление звука в среде, когда частота колебаний источника совпадает с одной из собственных частот колебания среды. Длина возникающей стоячей волны, как и собственная частота, зависит от длин столба воздуха. Таким образом, для получения резонанса мы должны подобрать такую длину 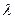 столба воздуха, чтобы длина стоячей волны в нём совпадала с длиной волны, распространяющейся от нашего источника звука.
столба воздуха, чтобы длина стоячей волны в нём совпадала с длиной волны, распространяющейся от нашего источника звука.
Из соотношения (10.9) следует, что наименьшая длина трубки, при которой наблюдается резонанс, должна равняться 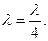
При постепенном увеличении длины 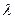 резонанс будет наблюдаться всякий раз, когда на длине воздушного столба уложится нечётное число четвертей длины волны:
резонанс будет наблюдаться всякий раз, когда на длине воздушного столба уложится нечётное число четвертей длины волны:
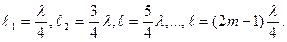
Зная частоту колебаний источника звука и определив длину волны 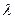 по длине воздушного столба в моменты резонанса, можно найти по формуле (10.10) скорость звука в воздухе.
по длине воздушного столба в моменты резонанса, можно найти по формуле (10.10) скорость звука в воздухе.
Но у открытого конца трубки всегда имеется некоторое смещение пучности, т.е. пучность стоячей волны неточно совпадает с открытым концом трубки. Более точное значение длины волны 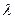 получим, рассматривая не абсолютные значения
получим, рассматривая не абсолютные значения 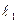 ,
, 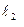 и т.д., а разности:
и т.д., а разности:
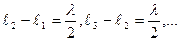 (10.11)
(10.11)
Отсюда найдём 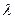 и, подставив её значение в формулу (10.10), определим скорость распространения звука в воздухе
и, подставив её значение в формулу (10.10), определим скорость распространения звука в воздухе 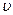 .
.
II. Выполнение измерений и обработка результатов.
Описание установки. Необходимый для опыта столб воздуха заключён в горизонтальной металлической трубе Кундта. Правое основание столба ограничено открытым концом трубы, левое – подвижным поршнем, который с помощью блока и нити может перемещаться вдоль трубы. Длина столба воздуха от открытого конца до поршня измеряется линейкой, укреплённой параллельно трубе.
- Обернуть ножку камертона “ля” мягким материалом и возбудить его ударами молоточка.
- Перемещая поршень вдоль трубы, отыскивать для него такие положения, при которых наблюдается значительное усиление звука. Наметив такие места, произвести более точную настройку, двигая поршень в небольших пределах на найденном участке. Камертон держать ближе к открытому концу трубы.
- Измерить длины воздушного столба
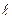 при резонансах и вычислить длину волны.
при резонансах и вычислить длину волны. - Вычислить скорость распространения звука в воздухе при данной температуре, абсолютную и относительную погрешность полученного результата для “ля”.
- Определить методом резонанса длину звуковой волны от второго камертона
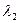 .
. - Определить частоту второго камертона по формуле:
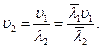
- Занести результаты в таблицу (10.1).
Таблица 10.1.
| N п/п | 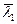 ,м (ля) ,м (ля) | 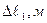 | 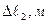 | 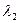 ,м (х) ,м (х) | 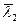 , м , м | 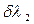 ,м ,м | 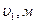 (ля) (ля) | 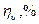 | 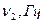 (х) (х) |
| 1. | |||||||||
| 2. | |||||||||
| 3. |
Контрольные вопросы.
- Как образуется стоячая волна?
- Что такое длина волны?
- Что понимают под узлами и пучностями стоячей волны?
- В каком соотношении находятся длина волны с координатами пучностей и узлов?
- Что такое резонанс?
- В каких местах воздушного столба при втором резонансе частицы воздуха колеблются с наибольшей амплитудой?
Какова у них разность фаз?
- В каких местах амплитуда равна нулю?
- В каких местах фазы колебаний частицы совпадают? Где они противоположны?
- В каких местах амплитуды равны, а фазы противоположны?
- Если первый резонанс воздушного столба определённой длины возникает на частоте 440 Гц, то на каких других частотах также должен наблюдаться резонанс?
